一、定义

1、任务

根据语法规则（即语言的文法），分析并识别出各种语法成分，如表达式、各种说明、各种语句、过程、函数等，并进行语法正确性检查

2、对比

词法分析：3型（正则文法） 词法分析：字符串
语法分析：2型（上下文无关文法） 语法分析：符号串

3、方法

1. 自顶向下（Top-Down）分析：推导（Derivations）
   若$Z={>}^{+}S则S\in L(G[Z])否则S\notin L(G[Z])$
2. 自底向上（Bottom-Up）分析：规约（Reductions）
   若$Z<{=}^{+}S则S\in L(G[Z])否则S\notin L(G[Z])$

本节主要分析自顶向下方法

4、自顶向下面临问题

推导顺序：有多个“非终结符”，优先用哪个？
避免二义性：避免文法有多个可用规则。

问题：左递归问题+回溯问题
常见方法：递归子程序法+LL分析法

二、自顶向下分析

1、概念

给定符号串S，若预测是某一语法成分，则可根据该语法成分的文法,设法为S构造一棵语法树，若成功,则S最终被识别为某一语法成分,即$S\in L(G[Z])$，其中G[Z]为某语法成分的文法。若不成功, 则 $S\notin L(G[Z])$

2、特点

1. 分析过程是带预测的，对输入符号串要预测属于什么语法成分，然后根据该语法成分的文法建立语法树。
2. 分析过程是一种试探过程，是尽一切办法(选用不同规则) 来建立语法树的过程, 由于是试探过程, 难免有失败, 所以分析过程需进行回溯, 因此也称这种方法是带回溯的自顶向下分析方法。
3. 最左推导可以编写程序来实现, 但带溯的自顶向下分析方法在实际上价值不大, 效率低。

3、二义性问题

若对于一个文法的某一句子（或句型）存在两棵不同的语法树，则该文法是二义性文法，否则是无二义性文法。

若一个文法的某句子存在两个不同的规范推导，则该文法是二义性的，否则是无二义性的。

若一个文法的某规范句型的句柄不唯一，则该文法是二义性的，否则是无二义性的。

PS：正则文法也会有二义性，但是可判定的（通过转换为自动机）

文法的二义性是不可判定的，因此解决方法是提出一些限制条件，称为无二义性的充分条件，当文法满足这些条件时，就可以判定文法是无二义性的。

4、左递归问题

1）概念

令U是文法的任一非终结符，文法中有规则$U::=U\cdot \cdot \cdot \cdot 或者U=>U\cdot \cdot \cdot$

自顶向下分析的基本缺点是：不能处理具有左递归性的文法。
（如果在匹配输入串的过程中，假定正好轮到要用非终结符U直接匹配输入串，即要用U的右部符号串U¨¨去匹配，为了用U¨¨去匹配，又得用U去匹配，这样无限的循环下
去将无法终止。）

2）消除

1. 使用扩充的BNF表示来改写文法
   (1)$E::=E+T|T=>E::=T${$+T$}
   (2) $T::=T\ast F|T/F|F=>T::=F${$\ast F|/F$}

具体规则：
提因子：若：$U::=xy|xw|\dots .|xz则可改写为：U::=x(y|w|\dots .|z)$

若有文法规则：$U::=x|y|\dots \dots |z|Uv可以改写为U::=(x|y|\dots \dots |z)${$v$}
其特点是：具有一个直接左递归的右部并位于最后，这表明该语法类U是由x或y……或z其后随有零个或多个v组成。
通过以上两条规则，就能消除文法的直接左递归，并保持文法的等价性。

2. 将左递归规则改为右递归规则
   若：$P::=Pa|b$ 则可改写为：$P::=bP’P’::=aP’|\epsilon$
   

3）间接左递归

此时需要代入成直接左递归后再处理

1. 检查规则R是否存在直接左递归 $R::=Sa|a$
2. 把R代入Q的有关选择，改写规则Q $Q::=Sab|ab|b$
3. 检查Q是否存在直接左递归
4. 把Q代入S的右部选择 $S::=Sabc|abc|bc|c$
5. 消除S的直接左递归 $S::=(abc|bc|c)${$abc$}

5、回溯问题

1）概念

概念：分析工作要部分地或全部地退回去。

造成回溯的条件：文法中，对于某个非终结符号的规则其右部有多个选择，并根据所面临的输入符号不能准确地确定所要的选择时，就可能出现回溯。

2）消除

对于$U::={\alpha }_1|{\alpha }_2|{\alpha }_3$
定义：$FIRST({\alpha }_i)=${$a|{\alpha }_i={>}^{\ast }a\dots ,a\in V_t$}
为了避免回溯，对文法的要求是：$FIRST({\alpha }_i)\cap FIRST({\alpha }_j)=\phi (i\ne j)$

3）解决方法

1. 改写文法
   判断后若有相交，则需要把相交的部分提出放到高一级的文法中，如下例子：
   
2. 超前扫描（偷看）
   当文法不满足避免回溯的条件时，即各选择的首符号相交时，可以采用超前扫描的方法，即向前侦察各输入符号串的第二个、第三个符号来确定要选择的目标。

这种方法是通过向前多看几个符号来确定所选择的目标，从本质上来讲也有回溯的味道，因此比第一种方法费时，但是假读仅仅是向前侦察情况，不作任何语义处理工作

6、总结

为了在不采取超前扫描的前提下实现不带回溯的自顶向下分析，文法需要满足两个条件：

1. 文法是非左递归的
2. 对文法的任一非终结符，若其规则右部有多个选择时， 各选择所推出的终结符号串的首符号集合要两两不相交。

在上述条件下，就可以根据文法构造有效的、不带回溯的自顶向下分析器。

对于第二点，我们只有$FIRST$集合是不够的：
定义$FOLLOW(A)=${$a|Z={>}^{\ast }\dots Aa\dots ，a\in V_t$}
$A\in V_n$ 该集合称为A的后继符号集合
特殊地：$若Z={>}^{\ast }...A$ 则 # $\in FOLLOW(A)$

不带回溯的充分必要条件是：对于G的
每一个非终结符A的任意两条规则$A::=\alpha |\beta$,下列条件成立：

1. $FIRST(\alpha )\cap FIRST(\beta )=Ф$
2. $若\beta =={>}^{\ast }\epsilon ,则FIRST(\alpha )\cap FOLLOW(A)=Ф$

三、递归子程序法（递归下降分析法）

1、概念

具体做法：对语法的每一个非终结符都编一个分析程序，当根据文法和当时的输入符号预测到要用某个非终结符去匹配输入串时，就调用该非终结符的分析程序

2、具体做法

1. 检查并改写文法
   
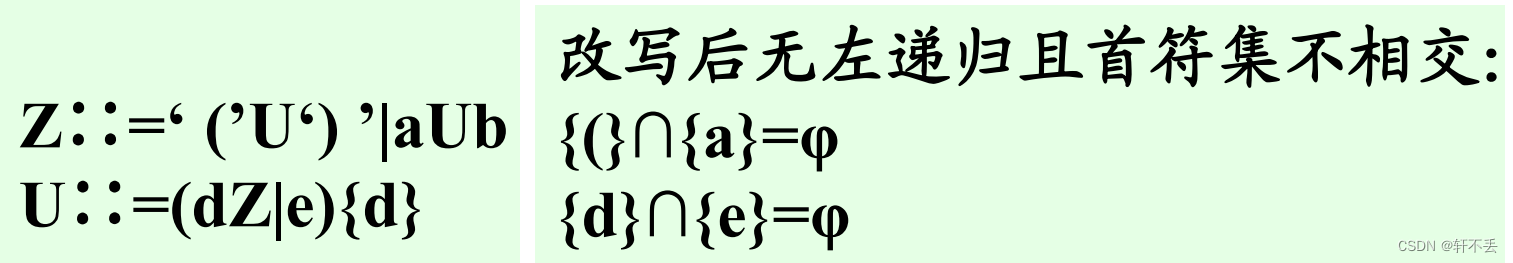
2. 检查文法的递归性
   
   因此，Z和U的分析程序要编成递归子程序
3. 算法框图
   非终结符号的分析子程序的功能是：用规则右部符号串去匹配输入串
   
   

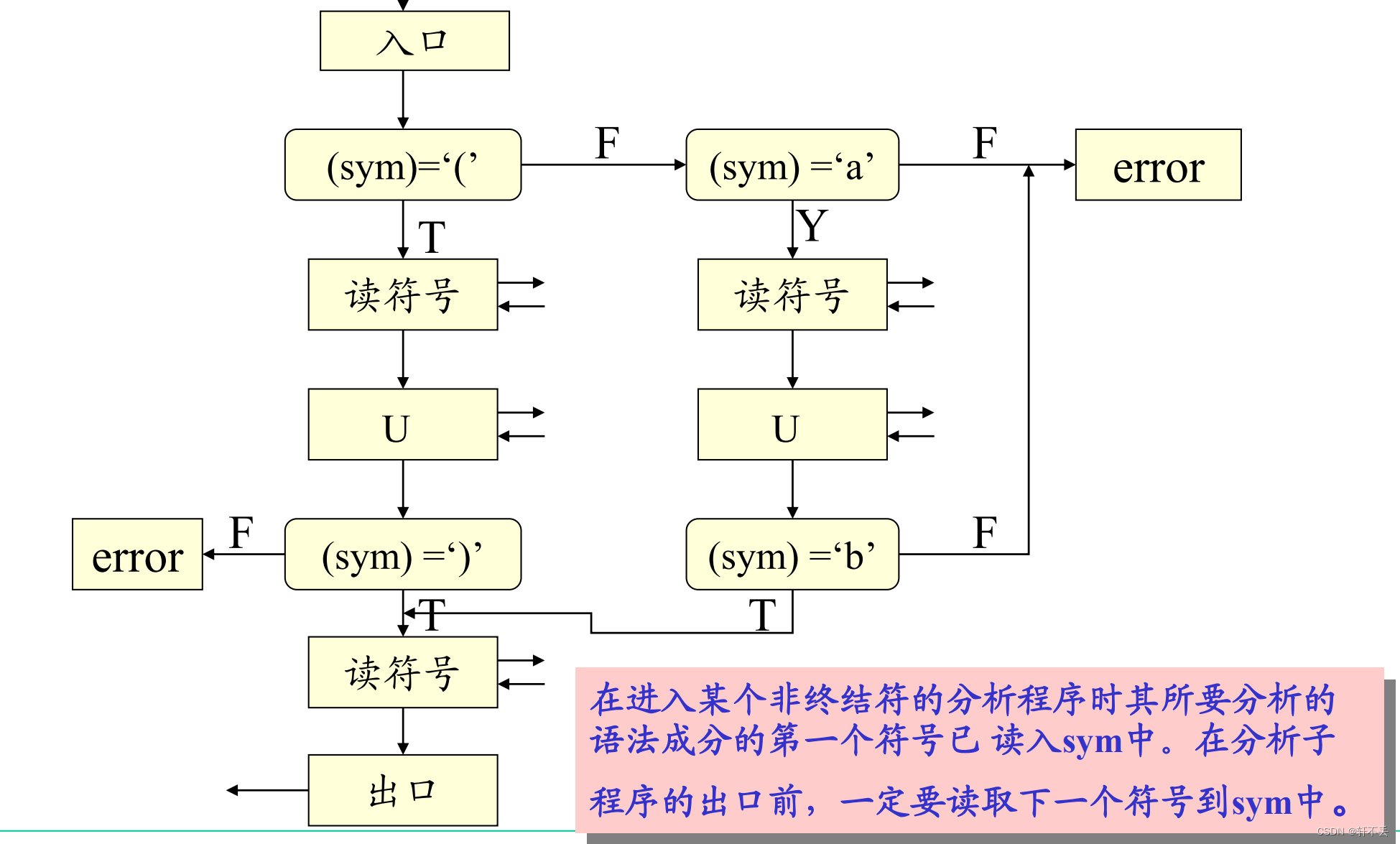
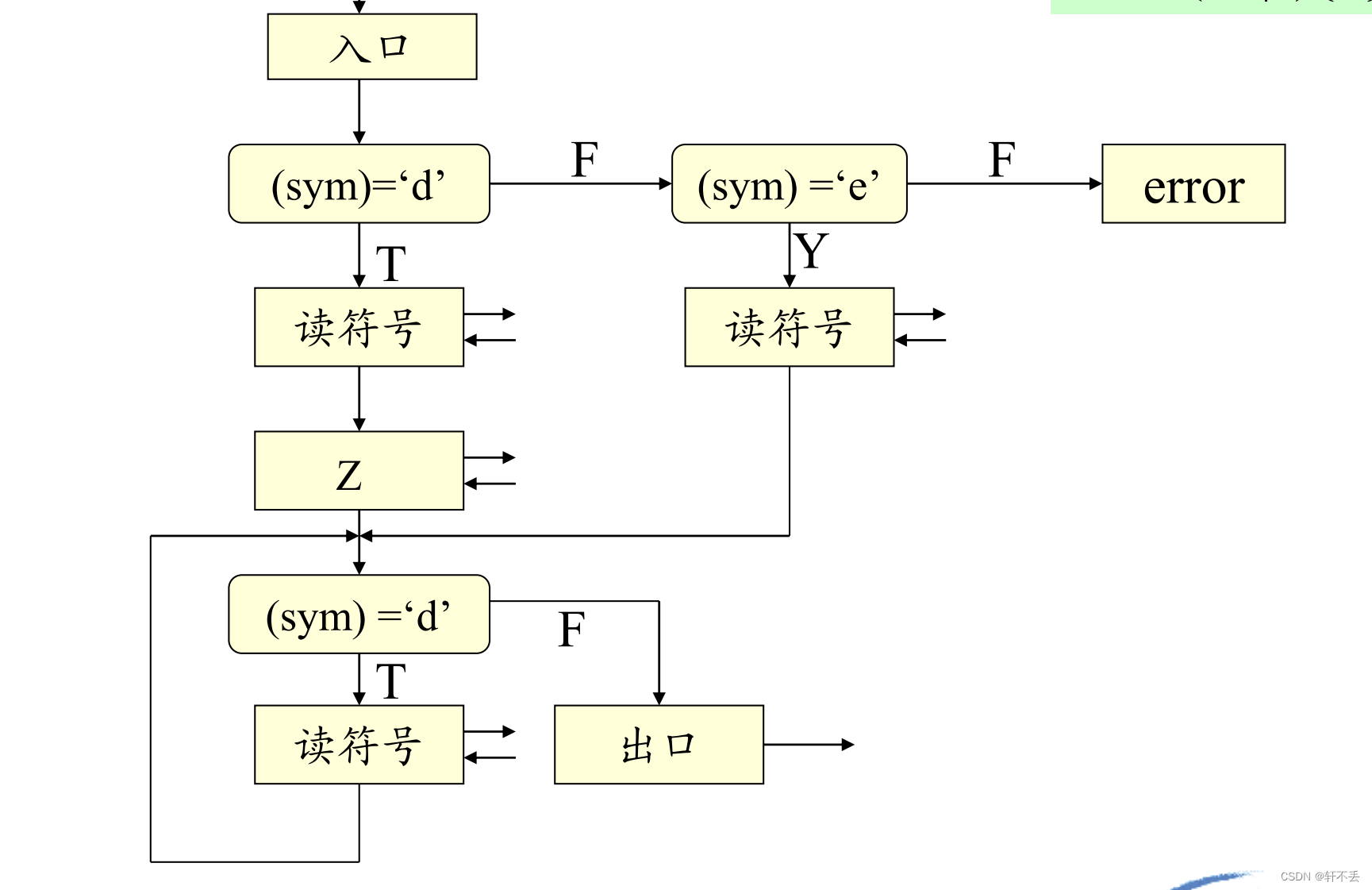
要注意子程序之间的接口,在程序编制时进入某个非终结符的分析程序时其所要分析的语法成分的第一个符号已读入sym中。

递归子程序法对应的是最左推导过程

四、LL(1)文法

1、预备知识

1）FIRST集的计算

$FIRST({\alpha }_i)=${$a|{\alpha }_i={>}^{\ast }a\dots ,a\in V_t$}
若$\alpha ={>}^{\ast }\epsilon ，则\epsilon \in FIRST(\alpha )$

设$\alpha =X_1{X}_2...X_n,X_i\in V_{n}U{V}_t（即X_i\in V)$
首先求出组成α的每一个符号$X_i$的FIRST集合


注意：要顺序往下做，一旦不满足条件，过程就要中断进行
得到$FIRST(X_i)，即可求出FIRST(\alpha )$

2）FOLLOW的算法

算法：连续使用以下规则，直至FOLLOW集合不再扩大

2、LL(1)文法的概念

第一个L：从左向右分析 (Left to right)
第二个L：产生“最左推导”(Left-most derivation)
k=1：向前查看“k=1”个符号，通过向前看1个符号就能够有效分析
无二义，无左递归，且能够消除回溯
因此判断LL(1)文法的条件就是为了在不采取超前扫描的前提下实现不带回溯的自顶向下分析所满足的条件
无左递归且

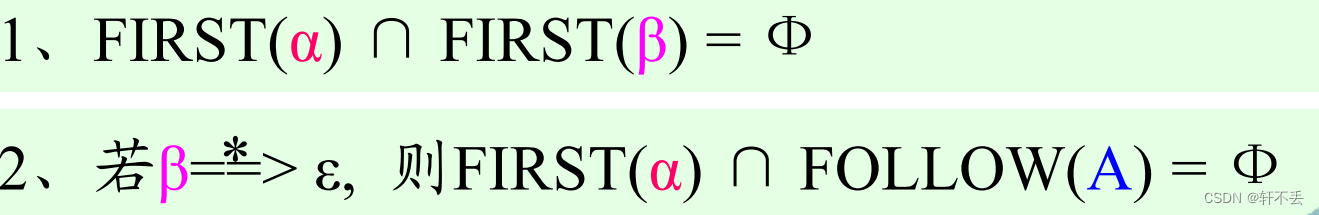
3、分析

1）组成

由三部分组成

1. 分析表
2. 执行程序 (总控程序）
3. 符号栈 （分析栈）
   
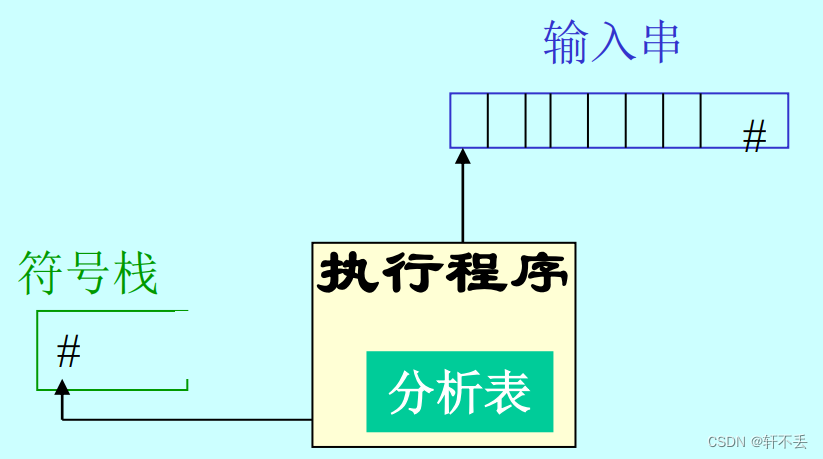
   在实际语言中，每一种语法成分都有确定的左右界符，为了研究问题方便，统一以‘＃’表示。

2）分析表

算法：

3）符号栈

四种状态

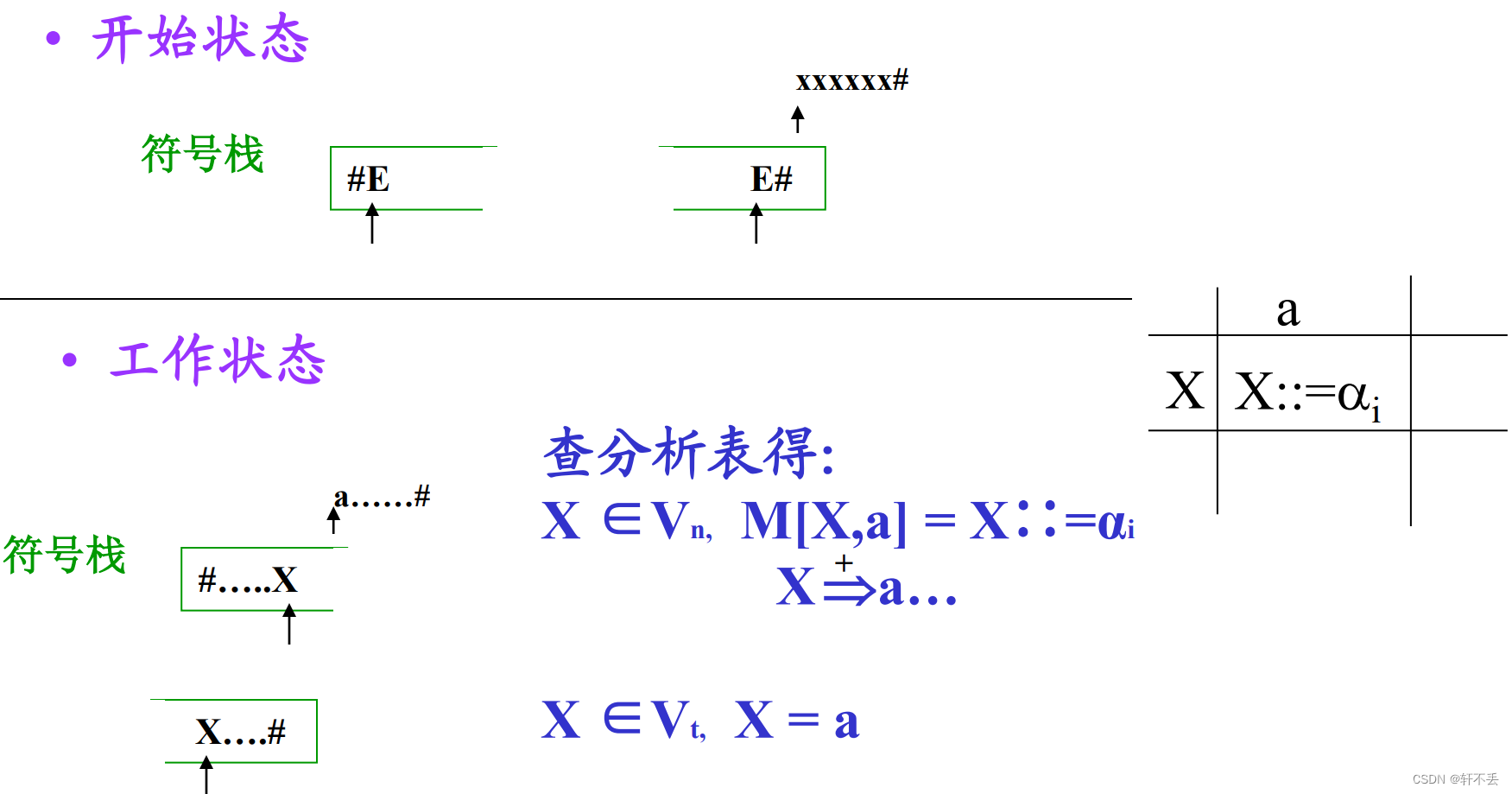
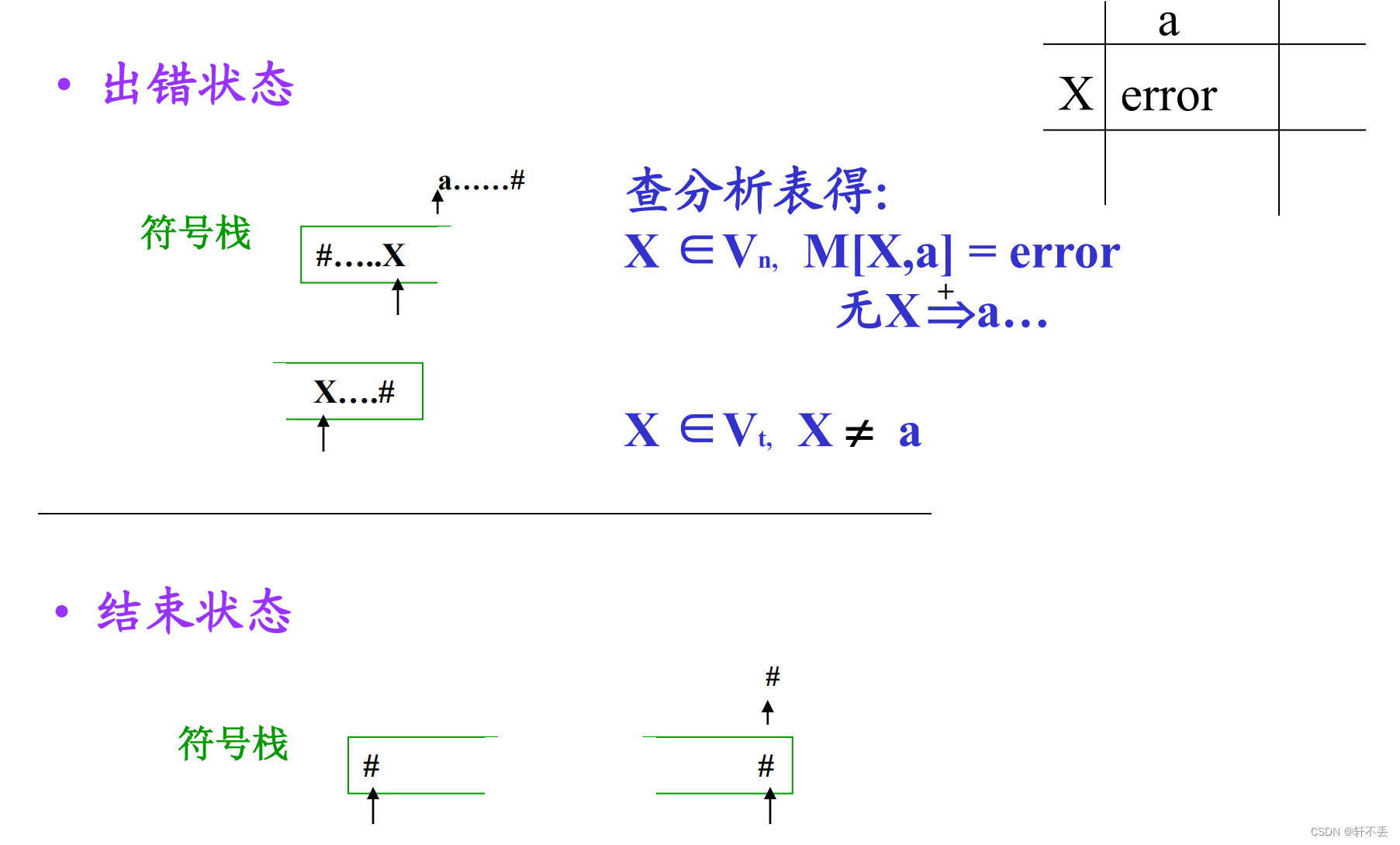
4）执行程序

主要实现如下操作

1. 把#和文法识别符号E推进栈, 读入下一个符号，重复下述过程直到正常结束或出错。
2. 测定栈顶符号X和当前输入符号a,执行如下操作:
   若KaTeX parse error: Expected 'EOF', got '#' at position 5: X=a=#̲，分析成功，停止。E匹配输入串成功。
   若KaTeX parse error: Expected 'EOF', got '#' at position 5: X=a≠#̲，把X推出栈，再读入下一个符号。
   若$X\in V_n$，查分析表M。
   注意a)中U在栈顶！

PS：文法没有 x→ε，则不需要计算 FOLLOW 集！！！！

五、LL(k)文法

LL(k)是无二义性的文法，其识别的语言都是确定型下推自动机所识别的语言，但反之不能保证一个确定型下推自动机与LL(k)等价。因此关系图如下：
一个无二义的CFG文法不一定能得到LL(k)文法

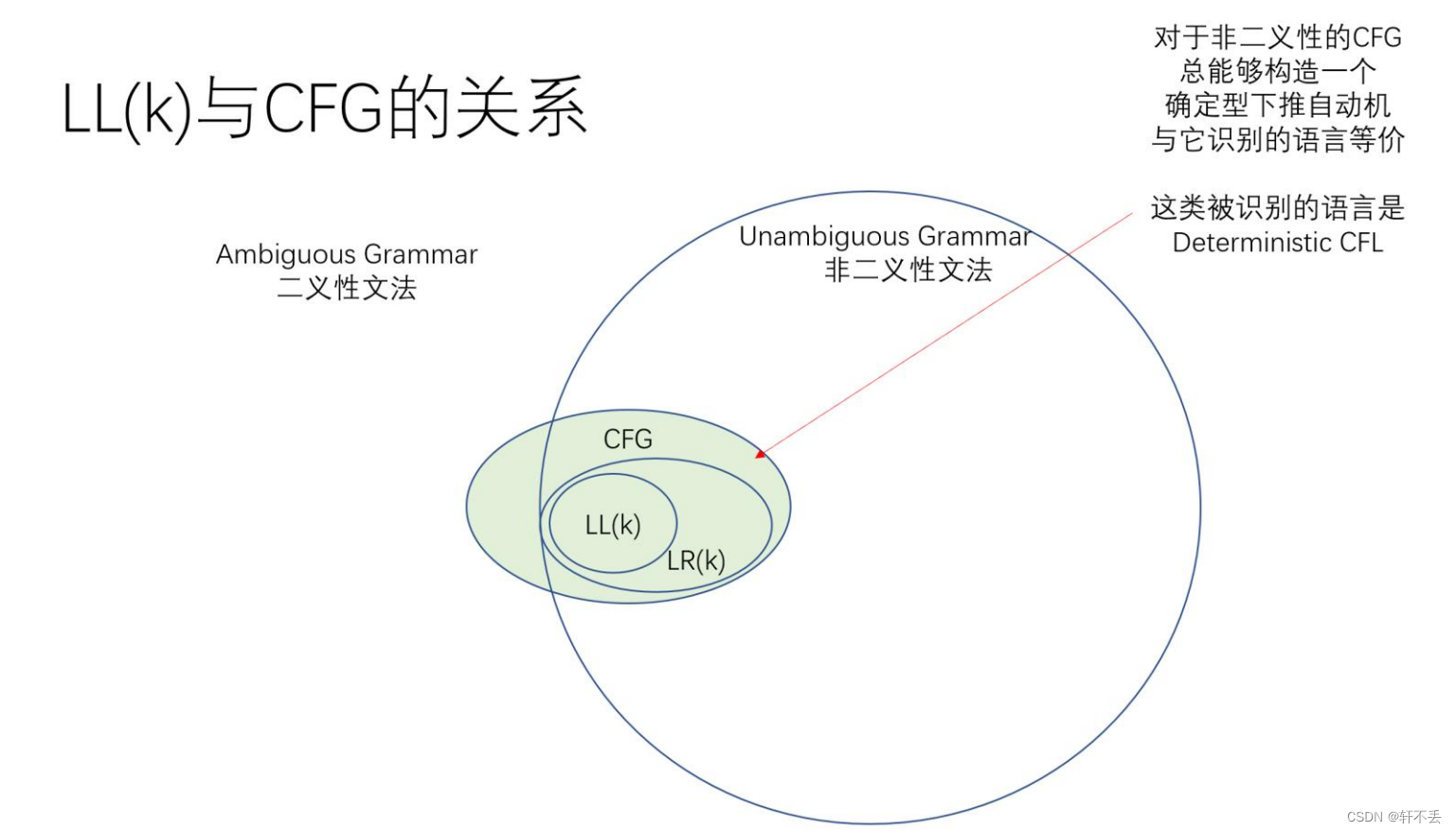
LL(k)文法总是一个LR(k)文法