一个数字电路就像一所城市的交通，晶振的作用就是十字路口的信号灯，因此晶振的品质及其电路应用尤其关键。数字电路又像生命体，它的运行就像人身体里的血液流通，它不是由单一的某个器件或器件单元构成，而是由多个器件及程序彼此配合、协调，共同完成良性的运转。

晶振频偏计算公式如下：

常见MHz晶振精度PPM值一般为±10PPM；±20PPM；±30PPM

若温度频差为±12PPM，则频率变化计算如下：

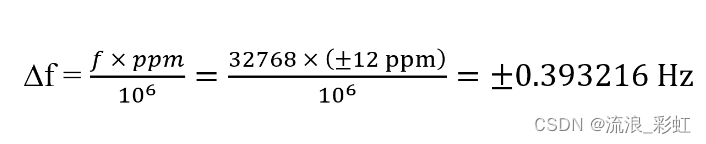
PPM是英文Parts Per Million的缩写，表示百万分之几。换句话说：1PPM则代表百万分之一的误差。

举例：若一颗晶振为12.000000MHz，即：12000000Hz
精度为±30ppm，那么误差频率为：30/100万12M=360Hz
精度为±20ppm，那么误差频率为：20/100万12M=240Hz
精度为±10ppm，那么误差频率为：20/100万*12M=120Hz
由此可见，系统时钟准确度与晶振PPM值（频率精度）紧密相关。晶振PPM等级分为±0.2PPM、±0.5PPM、±2PPM、±5PPM、±10PPM、±20PPM、±30PPM等。
 

32.768KHz时钟RTC晶振精度PPM值及频差范围（含时间误差）：

针对于RTC时钟晶振32.768KHz的频率精度, 则另有算法,32.768KHz晶振计时公式如下：

举例：若晶振32.768KHz精度为±10PPM，一天时间误差计算公式如下：

10(PPM)×24(1天=24小时)×60（1小时=60分钟）×60（1分钟=60秒）=864000*1/1000000=0.864秒

即：该RTC晶振每天的时间误差不超过0.864秒，即：若为+10PPM，每天最多快0.864秒，若为-10PPM，每天最多慢0.864秒。

RTC时钟晶振32.768KHz时间误差：

±10PPM：频差为：32768.32768Hz~32767.67232Hz，每天时间误差为0.864×1=0.864秒，月误差25.92秒，一年时间总偏差为5.184分钟。

±20PPM：频差为：32768.65536Hz~32767.34464Hz，每天时间误差为0.864×2=1.728秒，月误差51.84秒，一年时间总偏差为10.368分钟。

±30PPM：频差为：32768.98304Hz~32767.01696Hz，每天时间误差为0.864×3=2.592秒，月误差77.76秒，一年时间总偏差为15.552分钟