数据结构入门————树（C语言/零基础/小白/新手+模拟实现+例题讲解）

目录

1. 树的概念及其结构

        1.1 树的概念：

        1.2 树的相关概念：

        1.3 树的表示方法：

​编辑

        1.4 树的应用：

2. 二叉树的概念及其结构        

        2.1 概念:

        2.2 特点：

        2.3 特殊二叉树：

        2.4 二叉树的性质：

3. 二叉树的顺序存储结构 

        3.1 二叉树的顺序存储结构

        3.2 堆的概念及其结构

        3.3 堆的实现

4. 二叉树的链式存储

        4.1 前序 ，中序 ，后序遍历

        4.2 层序遍历

1. 树的概念及其结构

        1.1 树的概念：

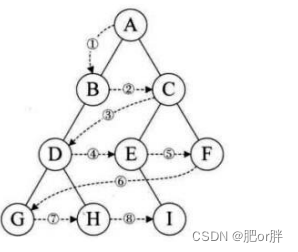
        树（Tree）是n（n>=0）个结点的有限集。n=0时称为空树。在任意一棵非空树中：1.有且仅有一个特定的称为根(Root)的结点；2.当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1,T2...，Tm，其中每一个集合本身又是一颗树，称为根的子树（Sub Tree）,如下图所示。

注：

        1. 子树是不相交的。

        2. 除了根节点以外，每个节点有且只有一个父节点

        3. 一棵有N个节点的树有N-1条边。

        1.2 树的相关概念：

     a.结点的分类

        结点的度：结点拥有的子树的个数。例如，A的度为6。

        树的度：最大结点的度为树的度。例如，上图结点的度为6,。

        叶结点/终端结点：度为0的结点。例如，结点B。

       非终端结点/分支结点：度不为0的结点。例如，结点D,E....

    b.结点的关系

        双亲结点/父结点：若一个结点含有子结点，那么该结点就是父结点。例如,A是B的父结点。

        孩子结点/子结点：结点子树的根称为该结点的孩子(Child)。例如,B是A的孩子。

        兄弟结点：具有相同父结点的结点称为兄弟结点。例如,B和C是兄弟结点。

        堂兄弟结点：双亲在同一层的结点称为堂兄弟结点。例如,H和I是堂兄弟结点。

        结点的祖先：从根结点到该结点的分支上的所有结点，称为该结点的祖先。例如，A时所有结点的祖先

        子孙：以某结点为根的子树中的任意结点都是该结点的子孙，例如，所有结点都是A的子孙。

    c.树的相关概念

        结点的层次：从根结点开始定义，根结点为第1层，根结点的子结点为第2层，以此类推。

        树的高度或深度：树中结点的最大层次。上图，树的高度为4。

        森林：由m棵互不相交的树的集合称为森林。

        1.3 树的表示方法：

                这里我们简单了解一下比较常用的：孩子兄弟表示法。

typedef int DataType;
struct Node
{struct Node*  LeftChild;    // 指向左边第一个孩子节点struct Node*  RightBrather; // 指向右边的兄弟节点DataType _data; // 结点中的数据域
};

        1.4 树的应用：

                我们在Linux系统中（操作系统的一种），使用的目录结构就是树状结构。

2. 二叉树的概念及其结构        

        2.1 概念:

                二叉树（Binary Tree）是n(n>=0)个结点的有限集，该集合或者为空集（空二叉树），或者由一个根结点和两棵互不相交的，分别称为根结点的左子树和右子树的二叉树组成。

        2.2 特点：

                a. 二叉树不存在度大于2的结点。

                b. 二叉树有左子树右子树之分，是有顺序的，不能颠倒，即使只有一棵子树，也要区分左子树还是右子树。

        2.3 特殊二叉树：

                a. 满二叉树：一个二叉树，每一层的结点数都达到最大值，则这个二叉树称为满二叉树。也就是说，如果一个满二叉树一共有h层，那么它的结点个数为 2^h-1。

                b. 完全二叉树：前h-1层结点数都达到最大值，最后一层不一定是满的，但一定从左往右有序。满二叉树是一个特殊的完全二叉树。

        2.4 二叉树的性质：

                1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^( i - 1 ) 个节点。 

                2. 若规定根节点的层数为1，则深度为h的二叉树的最大节点数是 2^( h )  - 1 。

                3. 对任何一棵二叉树，度为0的叶子节点个数为n0，度为2的分支节点个数为n2，则有n0 = n2 + 1。

                4. 若贵定根节点的层数为1，具有n个节点的满二叉树的深度，h = log₂(n + 1)。

                5. 对具有n个节点的完全二叉树，如果按照从上到下从左至右的数组顺序对所有节点开始编号，啧对于序号为i的节点有：

                a. 若 i > 0,i位置节点的双亲序号：(i - 1) / 2 ; i =0,i为根节点编号，无双亲节点。

                b. 若2 * i + 1 < n,左孩子序号： 2 * i + 1，若 2 * i + 1 >= n ,则无左孩子节点。

                c. 若2 * i + 2 < n,右孩子序号： 2 * i + 2，若 2 * i + 1 >= n,则无右孩子节点。 

1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ B ）
A 不存在这样的二叉树
B 200
C 198
D 199
解析：
叶子节点：度为0的节点，n0 = n2 +1
2. 在具有 2n 个结点的完全二叉树中，叶子结点个数为（ A ）
A n
B n+1
C n-1
D n/2
解析：
完全二叉树的节点度分为3种情况：度=1 or 度 =2 or 度 = 0；
2n = n0 + n1 + n2
n0 = n2 + 1 ,且 n1 = 0 或 n1 =0
2n0 + n1 = 2n    这里 n1只能为0 （偶数 + 奇数  !=  偶数）
所以叶子节点个数 = n
4.一棵完全二叉树的节点数位为531个，那么这棵树的高度为（ B ）
A 11
B 10
C 8
D 12
解析：
满二叉树的节点个数 = 2*h -1
完全二叉树中，叶子节点个数不确定，区间为：[ 2^( h - 1 ) + 1 , 2^( h ) -1 ]
将选项代入，得出高度为10
5.在一颗度为3的树中，度为3的结点有2个，度为2的结点有1个，度为1的结点有2个，则叶子结点有（  C ）个

A.4

B.5

C.6

D.7

解析：

        度为i的节点为ni，树的节点个数为n,则 n = n0 + n1 + n2 + n3;

        有n个节点的树的总边数为 ： n-1 条。

        根据度的定义，总边数 与 度 的关系: n -1 = 0 * n0 + 1 * n1 + 2 * n2 + 3 * n3

        联立方程可得，n0 = n2 +2 *n3 +1 , n0 = 6

3. 二叉树的顺序存储结构 

        3.1 二叉树的顺序存储结构

                普通的二叉树不适合用顺序存储结构，会造成大量空间浪费，但完全二叉树适合用顺序存储结构，现实中我们常把堆（一种二叉树）使用顺序结构存储。

        3.2 堆的概念及其结构

        堆中某个节点的值总是不大于或不小于其父节点的值；

        堆总是一棵完全二叉树。

        3.3 堆的实现

//Heap.h
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity; 
}Heap;// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);

#include "Heap.h"void Swap(HPDataType* x1, HPDataType* x2)
{HPDataType x = *x1;*x1 = *x2;*x2 = x;
}void AdjustDown(HPDataType* a, int n, int root)
{int parent = root;int child = parent*2+1;while (child < n){// 选左右孩纸中大的一个if (child+1 < n && a[child+1] > a[child]){++child;}//如果孩子大于父亲，进行调整交换 if(a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent*2+1;}else{break;}}
}void AdjustUp(HPDataType* a, int n, int child)
{int parent;assert(a);parent = (child-1)/2;//while (parent >= 0)while (child > 0){//如果孩子大于父亲，进行交换if (a[child] > a[parent]){Swap(&a[parent], &a[child]);child = parent;parent = (child-1)/2;}else{break;}}
}void HeapInit(Heap* hp, HPDataType* a, int n)
{int i;assert(hp && a);hp->_a = (HPDataType*)malloc(sizeof(HPDataType)*n);hp->_size = n;hp->_capacity = n;for (i = 0; i < n; ++i){hp->_a[i] = a[i];}// 建堆： 从最后一个非叶子节点开始进行调整// 最后一个非叶子节点，按照规则： （最后一个位置索引 - 1） / 2// 最后一个位置索引： n - 1// 故最后一个非叶子节点位置： (n - 2) / 2for(i = (n-2)/2; i >= 0; --i){AdjustDown(hp->_a, hp->_size, i);}
}void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_a = NULL;hp->_size = hp->_capacity = 0;
}void HeapPush(Heap* hp, HPDataType x)
{assert(hp);//检查容量if (hp->_size == hp->_capacity){hp->_capacity *= 2;hp->_a = (HPDataType*)realloc(hp->_a, sizeof(HPDataType)*hp->_capacity);}//尾插hp->_a[hp->_size] = x;hp->_size++;//向上调整AdjustUp(hp->_a, hp->_size, hp->_size-1);
}void HeapPop(Heap* hp)
{assert(hp);//交换Swap(&hp->_a[0], &hp->_a[hp->_size-1]);hp->_size--;//向下调整AdjustDown(hp->_a, hp->_size, 0);
}HPDataType HeapTop(Heap* hp)
{assert(hp);return hp->_a[0];
}int HeapSize(Heap* hp)
{return hp->_size;
}int HeapEmpty(Heap* hp)
{return hp->_size == 0 ? 0 : 1;
}void HeapPrint(Heap* hp)
{int i;for (i = 0; i < hp->_size; ++i){printf("%d ", hp->_a[i]);}printf("\n");
}

        

4. 二叉树的链式存储

        先来简单复习一下二叉树的概念，二叉树是：

        1. 空树

        2.非空：根节点，左子树，右子树组成

        从概念中可以看出，二叉树的定义是递归式的，因此后续基本操作都是按照该概念实现的。

        4.1 前序 ，中序 ，后序遍历

                二叉树遍历是按照某种特定的规则，依次对二叉树的节点进行相应的操作，并且每个节点只操作1次。

                按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

 1. 前序遍历（Preorder Traversal）:访问根节点的操作发生在遍历其左右子树之前。

 2. 后序遍历（Postorder Traversal）:访问根节点发生在遍历其左右子树之后。

 3. 中序遍历（Inorder Traversal）:访问根节点的操作发生在遍历其左右子树之间。

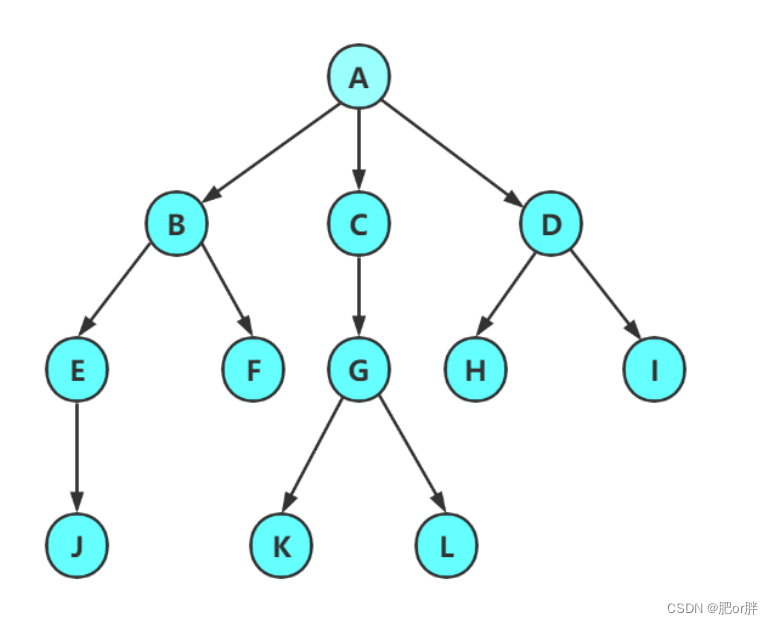
        4.2 层序遍历

 层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

                层序遍历中，我们使用队列来实现，但因为C语言的局限性，需要自己创建轮子，所以实现起来比较复杂，这里如果你对队列不太熟悉，可以参考下面这篇文章，帮助你更好的理解。

        

       数据结构入门————栈和队列（C语言/零基础/小白/新手+模拟实现+例题讲解）

//Tree.h
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);

#include "BTree.h"
#include "queue.h" //参考之前的代码
#include "stack.h"BTNode *BinaryTreeCreate(BTDataType * src, int n, int* pi)
{if (*pi >= n || src[*pi] == '#'){(*pi)++;return NULL;}BTNode * cur = (BTNode *)malloc(sizeof(BTNode));cur->_data = src[*pi];(*pi)++;cur->_left = BinaryTreeCreate(src, n, pi);cur->_right = BinaryTreeCreate(src, n, pi);return cur;
}void BinaryTreePrevOrder(BTNode* root)
{if (root){ putchar(root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);}
}void BinaryTreeInOrder(BTNode* root)
{if (root){BinaryTreeInOrder(root->_left);putchar(root->_data);BinaryTreeInOrder(root->_right);}
}void BinaryTreePostOrder(BTNode* root)
{if (root){BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);putchar(root->_data);}
}void BinaryTreeDestory(BTNode** root)
{if (*root){BinaryTreeDestory(&(*root)->_left);BinaryTreeDestory(&(*root)->_right);free(*root);*root = NULL;}
}void BinaryTreeLevelOrder(BTNode* root)
{Queue qu;BTNode * cur;QueueInit(&qu);QueuePush(&qu, root);while (!QueueIsEmpty(&qu)){cur = QueueTop(&qu);putchar(cur->_data);if (cur->_left){QueuePush(&qu, cur->_left);}if (cur->_right){QueuePush(&qu, cur->_right);}QueuePop(&qu);}QueueDestory(&qu);
}int BinaryTreeComplete(BTNode* root)
{Queue qu;BTNode * cur;int tag = 0;QueueInit(&qu);QueuePush(&qu, root);while (!QueueIsEmpty(&qu)){cur = QueueTop(&qu);putchar(cur->_data);if (cur->_right && !cur->_left){return 0;}if (tag && (cur->_right || cur->_left)){return 0;}if (cur->_left){QueuePush(&qu, cur->_left);}if (cur->_right){QueuePush(&qu, cur->_right);}else{tag = 1;}QueuePop(&qu);}QueueDestory(&qu);return 1;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/211365.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【深度学习】注意力机制（一）

【深度学习】注意力机制（一）

本文介绍一些注意力机制的实现&#xff0c;包括SE/ECA/GE/A2-Net/GC/CBAM。 目录 一、SE&#xff08;Squeeze-and-Excitation&#xff09; 二、ECA&#xff08;Efficient Channel Attention&#xff09; 三、GE&#xff08;Gather-Excite&#xff09; 四、A2-Net(Double A…
阅读更多...
二维码智慧门牌管理系统升级解决方案：数字鉴权

二维码智慧门牌管理系统升级解决方案：数字鉴权

文章目录 前言一、数字鉴权的核心机制二、数字鉴权的意义和应用 前言 随着科技的飞速发展&#xff0c;我们的生活逐渐进入数字化时代。在这个数字化的过程中&#xff0c;数据的安全性和门牌信息的保障变得至关重要。今天&#xff0c;我们要介绍的是二维码智慧门牌管理系统升级…
阅读更多...
【论文复现】zoedepth踩坑

【论文复现】zoedepth踩坑

注意模型IO&#xff1a; 保证输入、输出精度、类型与复现目标一致。 模型推理的代码 from torchvision import transforms def image_to_tensor(img_path, unsqueezeTrue):rgb transforms.ToTensor()(Image.open(img_path))if unsqueeze:rgb rgb.unsqueeze(0)return rgbdef…
阅读更多...
机器学习笔记 - 基于C# + .net framework 4.8的ONNX Runtime进行分类推理

机器学习笔记 - 基于C# + .net framework 4.8的ONNX Runtime进行分类推理

该示例是从官方抄的，演示了如何使用 Onnx Runtime C# API 运行预训练的 ResNet50 v2 ONNX 模型。 我这里的环境基于.net framework 4.8的一个winform项目，主要依赖下面版本的相关库。 Microsoft.Bcl.Numerics.8.0.0 Microsoft.ML.OnnxRuntime.Gpu.1.16.3 SixLabors.ImageShar…
阅读更多...
MyString：string类的模拟实现 1

MyString：string类的模拟实现 1

MyString&#xff1a;string类的模拟实现 前言&#xff1a; 为了区分标准库中的string&#xff0c;避免编译冲突&#xff0c;使用命名空间 MyString。 namespace MyString {class string{private:char* _str;size_t _size;size_t _capacity;const static size_t npos -1;// C标…
阅读更多...
2023年 - 我的程序员之旅和成长故事

2023年 - 我的程序员之旅和成长故事

2023年 - 我的程序员之旅和成长故事 &#x1f525; 1.前言 大家好&#xff0c;我是Leo哥&#x1fae3;&#x1fae3;&#x1fae3;&#xff0c;今天咱们不聊技术&#xff0c;聊聊我自己&#xff0c;聊聊我从2023年年初到现在的一些经历和故事&#xff0c;我也很愿意我的故事分…
阅读更多...
Android 样式小结

Android 样式小结

关于作者&#xff1a;CSDN内容合伙人、技术专家&#xff0c; 从零开始做日活千万级APP。 专注于分享各领域原创系列文章 &#xff0c;擅长java后端、移动开发、商业变现、人工智能等&#xff0c;希望大家多多支持。 目录 一、导读二、概览三、使用3.1 创建并应用样式3.2 创建并…
阅读更多...
【精彩回顾】恒拓高科亮相第十一届深圳军博会

【精彩回顾】恒拓高科亮相第十一届深圳军博会

2023年12月6日-8日&#xff0c;由中国和平利用军工技术协会、全国工商联科技装备业商会、深圳市国防科技工业协会等单位主办以及政府相关部门支持&#xff0c;深圳企发展览有限公司承的“2023第11届中国&#xff08;深圳&#xff09;军民两用科技装备博览会&#xff08;深圳军博…
阅读更多...
02 CSS基础入门

02 CSS基础入门

文章目录 一、CSS介绍1. 简介2. 相关网站3. HTML引入方式 二、选择器1. 标签选择器2. 类选择器3. ID选择器4. 群组选择器 四、样式1. 字体样式2. 文本样式3. 边框样式4. 表格样式 五、模型和布局1. 盒子模型2. 网页布局 一、CSS介绍 1. 简介 CSS主要用于控制网页的外观&#…
阅读更多...
C#如何使用SqlSugar操作MySQL/SQL Server数据库

C#如何使用SqlSugar操作MySQL/SQL Server数据库

一. SqlSugar 连接MySQL数据库 public class MySqlCNHelper : Singleton<MySqlCNHelper>{public static SqlSugarClient CnDB;public void InitDB() {//--------------------MySQL--------------------CnDB new SqlSugarClient(new ConnectionConfig(){ConnectionString…
阅读更多...
玩转大数据12：大数据安全与隐私保护策略

玩转大数据12：大数据安全与隐私保护策略

1. 引言 大数据的快速发展&#xff0c;为各行各业带来了巨大的变革&#xff0c;也带来了新的安全和隐私挑战。大数据系统通常处理大量敏感数据&#xff0c;包括个人身份信息、财务信息、健康信息等。如果这些数据被泄露或滥用&#xff0c;可能会对个人、企业和社会造成严重的损…
阅读更多...
大数据Doris（三十五）：Unique模型（唯一主键）介绍

大数据Doris（三十五）：Unique模型（唯一主键）介绍

文章目录 Unique模型（唯一主键）介绍 一、创建doris表 二、插入数据
阅读更多...
【华为OD题库-076】执行时长/GPU算力-Java

【华为OD题库-076】执行时长/GPU算力-Java

题目 为了充分发挥GPU算力&#xff0c;需要尽可能多的将任务交给GPU执行&#xff0c;现在有一个任务数组&#xff0c;数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。 假设GPU最多一次执行n个任务&#xff0c;一次执行耗时1秒&#xff0c;在保证GPU不空闲情况下&…
阅读更多...
linux 应用开发笔记---【标准I/O库/文件属性及目录】

linux 应用开发笔记---【标准I/O库/文件属性及目录】

一&#xff0c;什么是标准I/O库 标准c库当中用于文件I/O操作相关的一套库函数&#xff0c;实用标准I/O需要包含头文件 二&#xff0c;文件I/O和标准I/O之间的区别 1.标准I/O是库函数&#xff0c;而文件I/O是系统调用 2.标准I/O是对文件I/O的封装 3.标准I/O相对于文件I/O具有更…
阅读更多...
SpringBoot 项目 Jar 包加密，防止反编译

SpringBoot 项目 Jar 包加密，防止反编译

1场景 最近项目要求部署到其他公司的服务器上&#xff0c;但是又不想将源码泄露出去。要求对正式环境的启动包进行安全性处理&#xff0c;防止客户直接通过反编译工具将代码反编译出来。 2方案 第一种方案使用代码混淆 采用proguard-maven-plugin插件 在单模块中此方案还算简…
阅读更多...
调用别人提供的接口无法通过try catch捕获异常(C#)，见鬼了

调用别人提供的接口无法通过try catch捕获异常(C#)，见鬼了

前几天做CA签名这个需求时发现一个很诡异的事情&#xff0c;CA签名调用的接口是由另外一个开发部门的同事(比较难沟通的那种人)封装并提供到我们这边的。我们这边只需要把数据准备好&#xff0c;然后调他封装的接口即可完成签名操作。但在测试过程中&#xff0c;发现他提供的接…
阅读更多...
[后端卷前端2]

[后端卷前端2]

绑定class 为什么需要样式绑定呢? 因为有些样式我们希望能够动态展示 看下面的例子: <template><div><p :class"{active:modifyFlag}">class样式绑定</p></div> </template><script>export default {name: "goo…
阅读更多...
人力资源服务展示网站作用有哪些

人力资源服务展示网站作用有哪些

就业劳务问题往往是不少人群关注的问题&#xff0c;每个城市都聚集着大量求业者&#xff0c;而人力资源管理公司每年也会新增不少&#xff0c;对求业者来说&#xff0c;通过人力资源公司可以快速便捷的找到所需工作&#xff0c;而对公司来说&#xff0c;市场大量用户可以带来收…
阅读更多...
C语言第十八集(动态内存管理)

C语言第十八集(动态内存管理)

1.malloc函数可以开辟一块空间,具体搜: 2.malloc函数申请的空间在内存的堆区 而且它只负责帮你申请空间,不负责帮你清理空间 3.free函数可以释放内存 4.free函数释放的是内存中的堆区,具体搜: 5.在free函数调用完后记得把对应的指针设为空指针 6.calloc函数跟malloc函数差…
阅读更多...
揭秘字符串的奥秘：探索String类的深层含义与源码解读

揭秘字符串的奥秘：探索String类的深层含义与源码解读

文章目录 一、导论1.1 引言&#xff1a;字符串在编程中的重要性1.2 目的&#xff1a;深入了解String类的内部机制 二、String类的设计哲学2.1 设计原则&#xff1a;为什么String类如此重要&#xff1f;2.2 字符串池的概念与作用 三、String类源码解析3.1 成员变量3.2 构造函数3…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023