目录
参考链接
前言
IOU(Intersection over Union)
优点
缺点
代码
存在的问题
GIOU(Generalized Intersection over Union)
来源
GIOU公式
实现代码
存在的问题
DIoU(Distance-IoU)
来源
DIOU公式
优点
实现代码
总结
参考链接
IoU系列(IoU, GIoU, DIoU, CIoU)_iou giou diou_PoomHey的博客-CSDN博客
详解IoU、GIoU、DIoU、CIoU、EIoU和DIoU-NMS_小Aer的博客-CSDN博客
【目标检测算法】IOU、GIOU、DIOU、CIOU与YOLOv5损失函数_yolov5 iou-CSDN博客
前言
IOU损失函数目前主要应用于目标检测的领域,其演变的过程如下:IOU --> GIOU --> DIOU -->CIOU损失函数,每一种损失函数都较上一种损失函数有所提升。下面来具体介绍这几种损失函数。
IOU(Intersection over Union)
IoU就是我们所说的交并比,是目标检测中最常用的指标,IOU Loss的定义是先求出预测框和真实框之间的交集和并集之比,再求负对数,但是在实际使用中我们常常将IOU Loss写成1-IOU。如果两个框重合则交并比等于1,Loss为0说明重合度非常高。IOU满足非负性、同一性、对称性、三角不等性,相比于L1/L2等损失函数还具有尺度不变性,不论box的尺度大小,输出的iou损失总是在0-1之间。所以能够较好的反映预测框与真实框的检测效果。
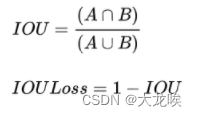
优点
- IOU具有尺度不变性,也就是对尺度不敏感(scale invariant), 在regression任务中,判断predict box和gt的距离最直接的指标就是IoU。
- 满足非负性;同一性;对称性;三角不等性
缺点
- 如果两个框没有相交,根据定义,IoU=0,不能反映两者的距离大小(重合度)。
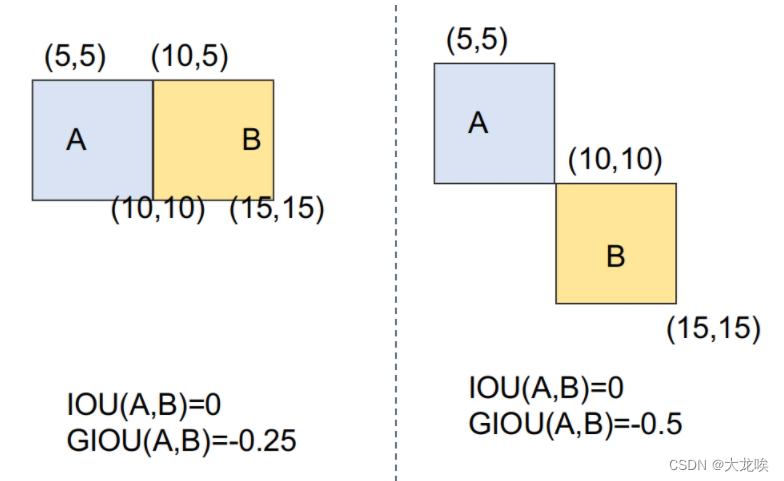
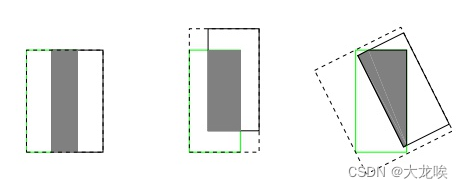
- IoU无法精确的反映两者的重合度大小。如下图所示,三种情况IoU都相等,但看得出来他们的重合度是不一样的,左边的图回归的效果最好,右边的最差。
代码
import numpy as np
def Iou(box1, box2, wh=False):if wh == False:xmin1, ymin1, xmax1, ymax1 = box1xmin2, ymin2, xmax2, ymax2 = box2else:xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1]-box2[3]/2.0)xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)# 获取矩形框交集对应的左上角和右下角的坐标(intersection)xx1 = np.max([xmin1, xmin2])yy1 = np.max([ymin1, ymin2])xx2 = np.min([xmax1, xmax2])yy2 = np.min([ymax1, ymax2]) # 计算两个矩形框面积area1 = (xmax1-xmin1) * (ymax1-ymin1) area2 = (xmax2-xmin2) * (ymax2-ymin2)inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1])) #计算交集面积iou = inter_area / (area1+area2-inter_area+1e-6) #计算交并比return iou
存在的问题
普通IOU是对两个框的距离不敏感的,如缺点一中的两个图中,左图预测框的坐标要比右图预测框的坐标更接近真实框。但两者的IOU皆为0,如果直接把IOU当作loss函数进行优化,则loss=0,没有梯度回传,所以无法进行训练。针对IOU的上述缺点GIOU应运而生
GIOU(Generalized Intersection over Union)
来源
在CVPR2019中,论文 《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》提出了GIoU的思想。由于IoU是比值的概念,对目标物体的scale是不敏感的。然而检测任务中的BBox的回归损失(MSE loss, l1-smooth loss等)优化和IoU优化不是完全等价的,而且 Ln 范数对物体的scale也比较敏感,IoU无法直接优化没有重叠的部分。

GIOU公式
GIOU公式如下:
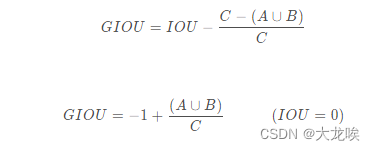
计算过程如下:
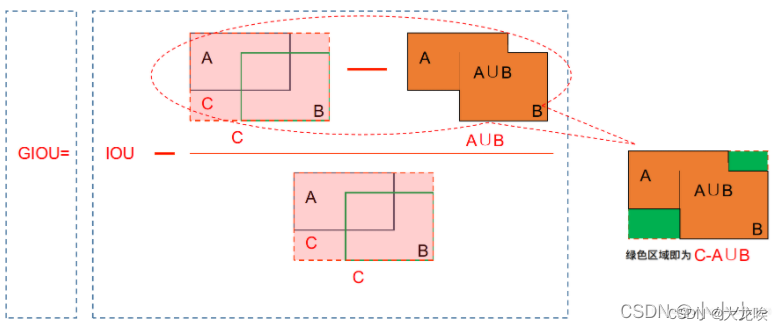
1.假设A为预测框,B为真实框,S是所有框的集合
2.不管A与B是否相交,C是包含A与B的最小框(包含A与B的最小凸闭合框),C也属于S集合
3.首先计算IoU,A与B的交并比
4.再计算C框中没有A与B的面积,比上C框面积;
5.IoU减去前面算出的比;得到GIoU
过程图示如下所示:
当IOU为0时,意味着A与B非常远时,
无限接近于0,GIOU趋近于-1,同理当IOU为1时,两框重合,
为1。所以GIOU的取值为(-1, 1]。
GIOU作为loss函数时,为L = 1 − GIOU ,当A、B两框不相交时A∪B值不变,最大化GIOU 就是就小化C,这样就会促使两个框不断靠近。
实现代码
def Giou(rec1,rec2):#分别是第一个矩形左右上下的坐标x1,x2,y1,y2 = rec1 x3,x4,y3,y4 = rec2iou = Iou(rec1,rec2)area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))area_1 = (x2-x1)*(y1-y2)area_2 = (x4-x3)*(y3-y4)sum_area = area_1 + area_2w1 = x2 - x1 #第一个矩形的宽w2 = x4 - x3 #第二个矩形的宽h1 = y1 - y2h2 = y3 - y4W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4) #交叉部分的宽H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4) #交叉部分的高Area = W*H #交叉的面积add_area = sum_area - Area #两矩形并集的面积end_area = (area_C - add_area)/area_C #闭包区域中不属于两个框的区域占闭包区域的比重giou = iou - end_areareturn giou
存在的问题
尽管GIoU解决了在IoU作为损失函数时梯度无法计算的问题,且加入了最小外包框作为惩罚项。但是它任然存在一些问题。下图第一行的三张图片是GIoU迭代时预测框收敛情况。其中黑色框代表anchor,蓝色框代表预测框,绿色框代表真实框。
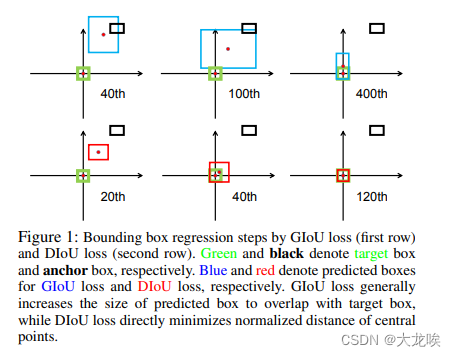
上图中可以看出,GIoU在开始的时候需要将检测结果方法使其与目标框相交,之后才开始缩小检测结果与GT重合,这就带来了需要较多的迭代次数才能收敛问题,特别是对于水平与垂直框的情况下。此外,其在一个框包含另一个框的情况下(),GIoU降退化成IoU,无法评价好坏,见下图所示:
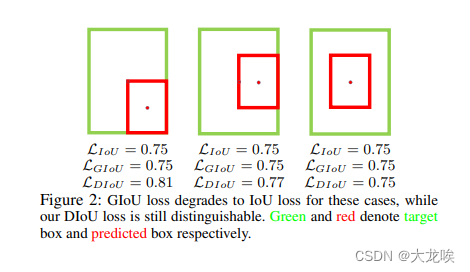
对此,DIOU又被提出
DIoU(Distance-IoU)
来源
针对上述GIOU的两个问题(预测框和真实框是包含关系的情况或者处于水平/垂直方向上,GIOU损失几乎已退化为IOU损失,即 |C - A U B | --> 0 ,导致收敛较慢)。有学者将GIOU中引入最小外接框来最大化重叠面积的惩罚项修改成最小化两个BBox中心点的标准化距离从而加速损失的收敛过程。该方法出自2020年AAAI 文章《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》
DIoU要比GIou更加符合目标框回归的机制,将目标与anchor之间的距离,重叠率以及尺度都考虑进去,使得目标框回归变得更加稳定,不会像IoU和GIoU一样出现训练过程中发散等问题。
DIOU公式
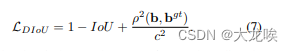
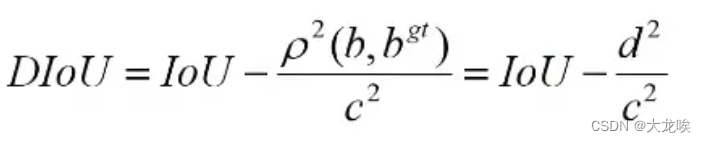
其中,![]() 分别代表了预测框与真实框的中心点,
分别代表了预测框与真实框的中心点,![]() 代表的是两个中心点之间的欧式距离,C代表的是能够同时包含预测框和真实框的最小闭包区域(最小外接矩形)的对角线距离。 如下图所示:
代表的是两个中心点之间的欧式距离,C代表的是能够同时包含预测框和真实框的最小闭包区域(最小外接矩形)的对角线距离。 如下图所示:
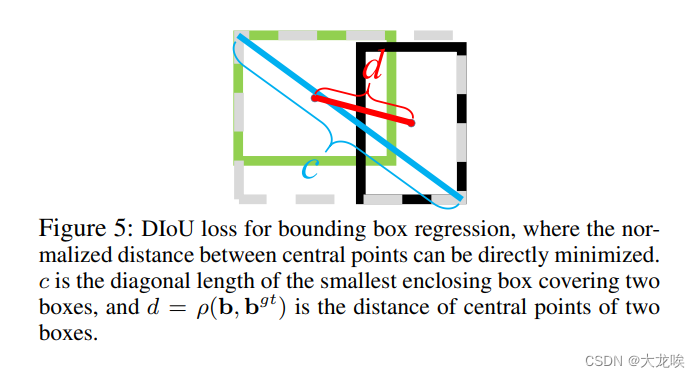
优点
- DIoU Loss的惩罚项能够直接最小化中心点间的距离,而且GIoU Loss旨在减少外界包围框的面积。
- DIoU与IoU,GIoU一样具有尺度不变性。
- DIoU与GIoU一样在与目标框不重叠时,仍然可以为边界框提供移动方向
- DIoU可以直接最小化两个目标框的距离,因此比GIoU Loss 收敛快得多
- DIoU在包含两个水平或垂直方向上的情况回归很快,而GIoU几乎退化为IoU。
实现代码
def Diou(bboxes1, bboxes2):rows = bboxes1.shape[0]cols = bboxes2.shape[0]dious = torch.zeros((rows, cols))if rows * cols == 0:#return diousexchange = Falseif bboxes1.shape[0] > bboxes2.shape[0]:bboxes1, bboxes2 = bboxes2, bboxes1dious = torch.zeros((cols, rows))exchange = True# #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]w1 = bboxes1[:, 2] - bboxes1[:, 0]h1 = bboxes1[:, 3] - bboxes1[:, 1] w2 = bboxes2[:, 2] - bboxes2[:, 0]h2 = bboxes2[:, 3] - bboxes2[:, 1]area1 = w1 * h1area2 = w2 * h2center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2 center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2 center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:]) inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2]) out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:]) out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)inter_area = inter[:, 0] * inter[:, 1]inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2outer = torch.clamp((out_max_xy - out_min_xy), min=0)outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)union = area1+area2-inter_areadious = inter_area / union - (inter_diag) / outer_diagdious = torch.clamp(dious,min=-1.0,max = 1.0)if exchange:dious = dious.Treturn dious
总结
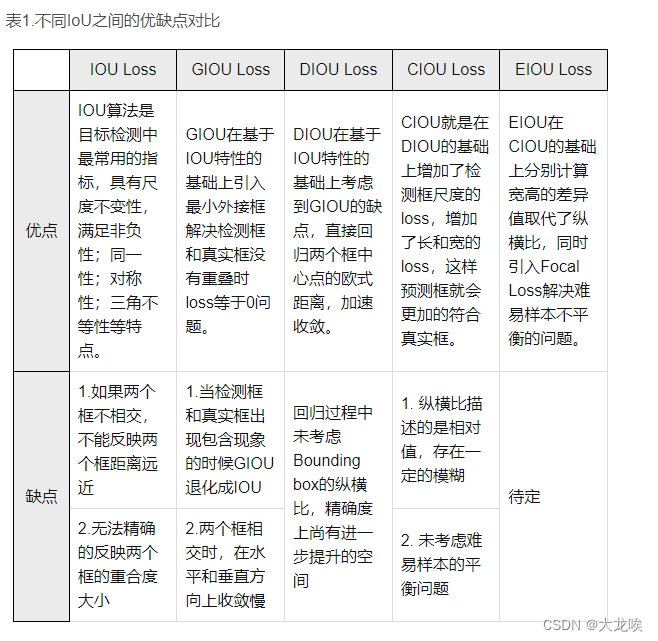
IOU、GIOU、DIOU、CIOU的对比
边界框回归的三大集合因素:重叠面积、中心点距离、纵横比
IoU: 考虑了重叠面积,归一化坐标尺度
GIoU: 考虑了重叠面积,基于IoU解决边界框不相交时loss等于0的问题。
DIoU: 考虑了重叠面积、中心点距离,基于IoU解决GIoU收敛慢的问题
CIoU: 考虑了重叠面积、中心点距离、纵横比,基于DIoU提升回归精确度
)









)
?)







