❤ IDEA导入项目并运行
Mac IDEA使用
(1) 仓库导入
通过获取giett仓库包的url,在idea中导入项目
- 在gitee里获取项目的ur
- 打开idea,点击 File->new->Project from Version Control
(2) 创建数据库ry并导入数据脚本
(3)修改配置文件
打开application-druid.yml配置文件(需要去配置文件中修改一下数据库链接。位置在 ruoyi-admin/src/main/resources/application-druid.yml
我本地的配置文件路径为
/Users/zthz/Downloads/RuoYi-Vue/home/logs
启动成功!
Mac 提示问题
提示Invalid path to Command Line Tools
查看Git的路径
which git
提示的路径信息是: /usr/local/bin/git
command +,快捷键打开设置,搜索git
输入地址
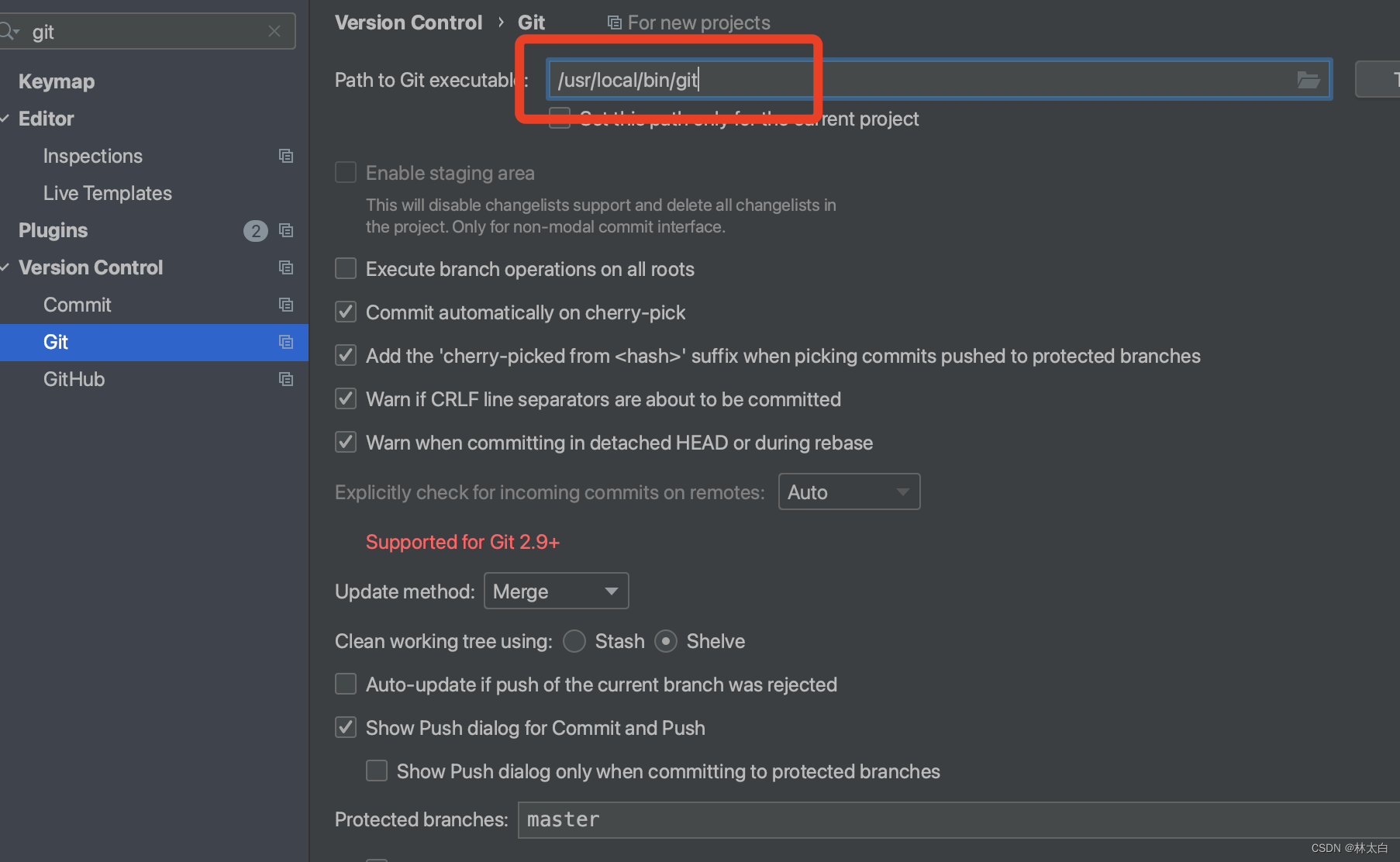
关闭再次打开,毫无问题


)















——沉浸式以及状态栏高)
