什么是建模语言
建模语言是一种描述信息或模型的编程语言,在运筹优化领域,一般是指代数建模语言。
比如要写一个线性规划问题的建模和求解,可以采用C、Python、Java等通用编程语言来实现计算机编程(码代码),也可以换采用建模语言。
本文将以阿里达摩院研发的MindOpt建模语言(MindOpt Algebra Programming Language, MindOptAPL,简称为MAPL)来讲解。MAPL是一种高效且通用的代数建模语言,当前主要用于数学规划问题的建模,并支持调用多种求解器求解。
代数建模语言工作原理
在数学规划领域,遇到一个实际问题时候,我们需要数学建模成优化问题模型、然后编程、然后计算优化结果,得到这个实际问题的解决方案。
在这个编程过程中,可以根据选用的计算工具——优化求解器提供的通用编程语言的API来编写代码,也可以采用建模语言来编写代码。如下示例,就是一个利用MAPL建模语言来进行一个优化问题码的代码。

- 左边是数学模型,三要素:两个变量xa和xb,目标函数是最大化一个公式,约束是最下面两行,限定取值关系。
- 中间是用MAPL建模语言编的代码。可以看到前面4行就表达清楚了左边的数学公式。最后“option solver mindopt;”是设置计算这个问题的求解器为mindopt求解器,“solve;”是执行求解。
- 右边就是求解器的计算结果,xa = 3,xb=5,此时目标函数最大,是1050。
为什么要用建模语言
语法更简单(代码对比)
从上面我们可以看到建模语言可以方便地进行数学建模和求解的代码。这里我们对比一下建模语言和通用的编程语言,来看看用建模语言优势。
以下面这个问题为示例:
| 线性规划模型:
max x0 + 2 * x1 + 3 * x2 + x3
s.t. (-1) * x0 + x1 + 3 * x2 + 10 * x3 <= 20
x0 - 3 * x1 + x2 = 30
x1 - 3.5 * x3 = 0
0 ≤ x0 ≤ 40
0 ≤ x1
0 ≤ x2
2 ≤ x3 ≤ 3
我们使用 MindOpt APL 建模语言 和 MindOpt 求解器的 Python APIs,分别对上面的线性规划模型建模,并求解模型。
MAPL代码:
clear model; #清除model,多次run的时候使用
option modelname test; #运行完代码之后会自动生成.nl和.sol文件 model是存放的地址,test是文件名#--------------------------
# twoTask.mapl
var x0 >= 0; # 声明决策变量xa |
var x1 >= 0;
var x2 >= 0;
var x3 >= 2;
maximize Reward: x0 + 2 * x1 + 3 * x2 + x3; # 声明目标函数
subto c1: (-1) * x0 + x1 + 3 * x2 + 10 * x3 <= 20; # 声明约束
subto c2: x0 - 3 * x1 + x2 <= 30;
subto c3: x1 - 3.5 * x3 == 0;
subto c4: x0 <= 40;
subto c5: x3 <= 3;
#--------------------------option solver mindopt; # (可选)指定求解用的求解器,默认是MindOpt
solve; # 求解print "-----------------Display---------------";
display; # 展示结果
print "目标函数值 = ",x0 + 2 * x1 + 3 * x2 + x3;
Python代码:
from mindoptpy import *if __name__ == "__main__":# Step 1. Create model.model = Model("test")try:# Step 2. Input model.# Change to minimization problem.model.ModelSense = MDO.MAXIMIZE# Add variables.x = []x.append(model.addVar(0.0, 40.0, 1.0, 'C', "x0"))x.append(model.addVar(0.0, float('inf'), 2.0, 'C', "x1"))x.append(model.addVar(0.0, float('inf'), 3.0, 'C', "x2"))x.append(model.addVar(2.0, 3.0, 1.0, 'C', "x3"))# Add constraints.model.addConstr(- 1.0 * x[0] + 1.0 * x[1] + 3.0 * x[2] + 10.0 * x[3] <= 20, "c1")model.addConstr(1.0 * x[0] - 3.0 * x[1] + x[2] <= 30, "c2")model.addConstr(1.0 * x[1] - 3.5 * x[3] == 0, "c3")# Step 3. Solve the problem and populate optimization result.model.optimize()if model.status == MDO.OPTIMAL:print(f"Optimal objective value is: {model.objval}")print("Decision variables: ")for v in x:print(f"x[{v.VarName}] = {v.X}")else:print("No feasible solution.")except MindoptError as e:print("Received Mindopt exception.")print(" - Code : {}".format(e.errno))print(" - Reason : {}".format(e.message))except Exception as e:print("Received other exception.")print(" - Reason : {}".format(e))finally:# Step 4. Free the model.model.dispose()
从上面的例子可以看到,MAPL建模语言比较简洁,没有Python运行这么多复杂的创建、添加、异常捕捉和释放的过程,就聚焦在编个模型去求解计算,更易于理解和添加。上面的例子还只是线性规划,对于非线性规划的问题,Python的API会更复杂。而采用MAPL建模语言只需要表达清楚数学公式,对于调试模型修改更方便。
支持多种求解器,换求解器的时候不用重复编程
很多人选择建模语言,最大的原因是希望切换求解器方案。因为不同品牌的求解器的求解能力不一样,遇到一个问题数学模型调整了一行公式,可能之前选择的求解器就不支持了,需要更换求解器。
此时如果选择用各家求解器的API来编程,换一个求解器,就需要重新学习对应的API,重新码代码,维护起来困难。虽然业界也有通用的 .mps 和 .nl 的优化问题数据格式,但是熟悉不同求解器的调用数据计算的方法也很耗时,或者装对应的软件也很麻烦。这个时候,建模语言的优势就很大。
比如下面是MAPL代码中,只需要换一行,就能换求解器进行计算:
option solver highs; # 更换求解器
更多MAPL支持的求解器,可以参考上一个博客MindOpt APL,可以支持调用几十种求解器的建模语言
建模语言也支持通用编程语言的API,如Python
有很多同学喜欢Python语言,更希望用Python编程。MAPL建模语言支持Python来调用,import maplpy后就用Python的方式来编代码,能继续享受一行代码换求解器的优良属性。可一看广告流量分配:曝光和转化均衡案例中的代码对比。
常见的建模语言
市面上的建模语言有很多个,需要看各家求解器支持的建模语言,比如MindOpt求解器支持如下4种建模语言:MAPL(MindOpt APL)、AMPL、Pyomo、PuLP。
其中MindOpt APL(MAPL)就是阿里达摩院自研的建模语言,是目前中国唯一一款代数建模语言。其他建模语言的描述大家可以点击上面的链接查看:https://opt.aliyun.com/platform/docs/htmldoc/solver
MAPL的优点
MAPL国内第一款拥有自主知识产权,完全自研的国产建模语言,提供了丰富文档学习以及案例参考。并且在电力SCUC等领域问题上建模性能优秀,对标或超越已有产品。对比AMPL等建模语言,部分语法上更灵活简单,后续也会支持向量化建模等特色能力,提升建模易用性等。
灵活性:
MAPL具有非常高的灵活性,可以用来建模和求解各种类型的优化问题,包括线性规划、整数规划、非线性规划等。它支持多种数学表达式和运算符,可以方便地表示复杂的数学关系和约束条件。如下是它支持数值计算。
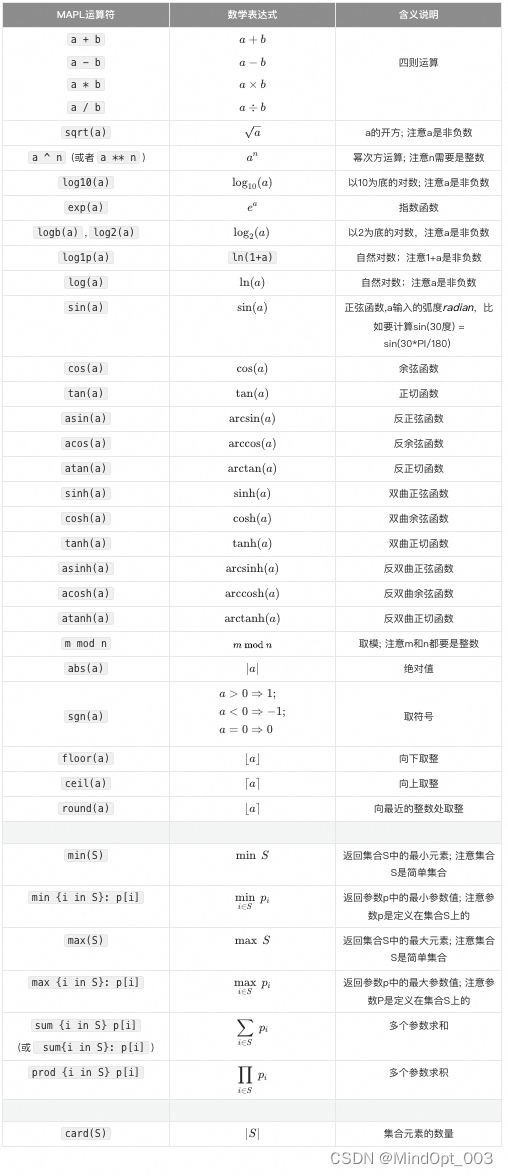
易用性
MAPL建模语言采用了类似于自然语言的语法和结构,使得用户可以很容易地理解和编写优化模型。并且支持读写csv文件,使得数据的读取和写入变得容易,数据储存也很方便。
如下将结果print输出为csv表格:
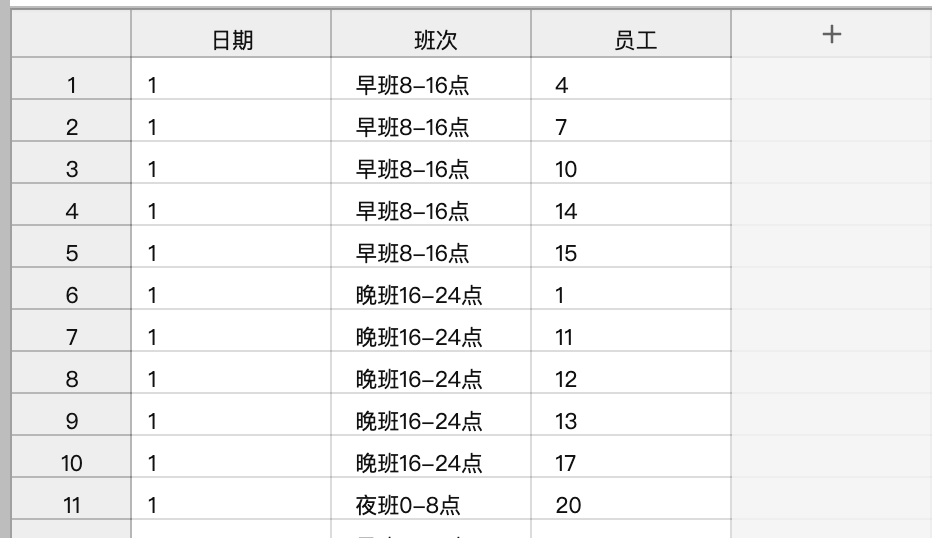
更多选择
MAPL与MindOpt Studio平台集成,可以在线上环境使用,无需下载,并且支持调用多种求解器,可直接对比结果。还支持将输出mps文件,可以在不同的计算环境和操作系统之间进行导入和导出。


——沉浸式以及状态栏高)





)

函数)
)






连接不同区域(Region)VPC)
