Multi-User in each Cell, MISO
沈闓明代码

Direct FP

K. Shen and W. Yu, “Fractional Programming for Communication Systems—Part I: Power Control and Beamforming,” in IEEE Transactions on Signal Processing, vol. 66, no. 10, pp. 2616-2630, 15 May15, 2018, doi: 10.1109/TSP.2018.2812733.

$\sum _{n=1}^N\sum _{k=1}^K{\log }_2\left(1+\frac{{|{\mathbf{h}}_{n,n,k}^H{\mathbf{w}}_{n,k}|}^2}{\sum _{(j,i)\ne (n,k)}{|{\mathbf{h}}_{j,n,k}^H{\mathbf{w}}_{j,i}|}^2+{\sigma }_{n,k}^2}\right)$
the direct FP approach applies the multidimensional quadratic transform (Theorem 2) to each SINR term.
$f_q\left(\mathbf{W},\mathbf{Y}\right)=\sum _{(n,k)}\log \left(1+2\mathrm{Re}\left\{y_{n,k}^H{\mathbf{w}}_{n,k}^H{\mathbf{h}}_{n,n,k}\right\}-{\left|y_{n,k}\right|}^2\left(\sum _{(j,i)\ne (n,k)}{\left|{\mathbf{h}}_{j,n,k}^H{\mathbf{w}}_{j,i}\right|}^2+{\sigma }_{n,k}^2\right)\right)$

初始化${\mathbf{w}}_{n,k},\forall n,k$
重复

1. 更新$y_{n,k}^{\star }=\frac{{\mathbf{h}}_{n,n,k}^H{\mathbf{w}}_{n,k}}{\sum _{(j,i)\ne (n,k)}{|{\mathbf{h}}_{j,n,k}^H{\mathbf{w}}_{j,i}|}^2+{\sigma }_{n,k}^2}$ with ${\mathbf{w}}_{n,k},\forall n,k$
2. 给定$y_{n,k}$，求解问题，更新${\mathbf{w}}_{n,k}$
   max ⁡ { w n , k , y n , k } f q ( W , Y ) s . t . ∑ k = 1 K w n , k H w n , k ≤ p ˉ n , ∀ n = 1 , … , N , \begin{array}{l} \mathop {\max }\limits_{\left\{ {{{\bf{w}}_{n,k}},{y_{n,k}}} \right\}} \;\;{f_q}\left( {{\bf{W}},{\bf{Y}}} \right)\\ {\rm{s}}.{\rm{t}}.\;\sum\limits_{k = 1}^K {{\bf{w}}_{n,k}^H{{\bf{w}}_{n,k}}} \le {{\bar p}_n},\forall n = 1, \ldots ,N, \end{array} {wn,k​,yn,k​}max​fq​(W,Y)s.t.k=1∑K​wn,kH​wn,k​≤pˉ​n​,∀n=1,…,N,​
   the optimization problem is a convex problem of ${\mathbf{w}}_{n,k}$ when the auxiliary variable $y_{n,k}$ is held fixed.

直到$f_q\left(\mathbf{W},\mathbf{Y}\right)$收敛

Closed-Form FP

K. Shen and W. Yu, “Fractional Programming for Communication Systems—Part I: Power Control and Beamforming,” in IEEE Transactions on Signal Processing, vol. 66, no. 10, pp. 2616-2630, 15 May15, 2018, doi: 10.1109/TSP.2018.2812733.

$\sum _{n=1}^N\sum _{k=1}^K{\log }_2\left(1+\frac{{|{\mathbf{h}}_{n,n,k}^H{\mathbf{w}}_{n,k}|}^2}{\sum _{(j,i)\ne (n,k)}{|{\mathbf{h}}_{j,n,k}^H{\mathbf{w}}_{j,i}|}^2+{\sigma }_{n,k}^2}\right)$
Lagrangian Dual Transform (Multidimensional and Complex)
$f_r\left(\mathbf{W},\mathbf{U}\right)=\sum _{(n,k)}\left(\log \left(1+u_{n,k}\right)-u_{n,k}+\left(1+u_{n,k}\right)\frac{{|{\mathbf{h}}_{n,n,k}^H{\mathbf{w}}_{n,k}|}^2}{\sum _{(j,i)}{|{\mathbf{h}}_{j,n,k}^H{\mathbf{w}}_{j,i}|}^2+{\sigma }_{n,k}^2}\right)$
$\frac{\partial }{\partial u_{n,k}}{f}_r\left(\mathbf{W},\mathbf{U}\right)=0$
$u_{n,k}^{\star }={\gamma }_{n,k}=\frac{{|{\mathbf{h}}_{n,n,k}^H{\mathbf{w}}_{n,k}|}^2}{\sum _{(j,i)\ne (n,k)}{|{\mathbf{h}}_{j,n,k}^H{\mathbf{w}}_{j,i}|}^2+{\sigma }_{n,k}^2}\in {\mathbb{R}}^1$
Quadratic Transform (Multidimensional)
$f_q\left(\mathbf{W},\mathbf{U},\mathbf{V}\right)=\sum _{(n,k)}\left(2\sqrt{(1+u_{n,k})}\mathrm{Re}\left\{{\mathbf{w}}_{n,k}^H{\mathbf{h}}_{n,n,k}{v}_{n,k}\right\}-{\left|v_{n,k}\right|}^2\left(\sum _{(j,i)}{\left|{\mathbf{h}}_{j,n,k}^H{\mathbf{w}}_{j,i}\right|}^2+{\sigma }_{n,k}^2\right)\right)+\mathrm{const}(\mathbf{U})$
$\frac{\partial }{\partial v_{n,k}}{f}_q\left(\mathbf{W},\mathbf{U},\mathbf{V}\right)=0$
$v_{n,k}^{\star }=\frac{\sqrt{(1+u_{n,k})}{\mathbf{h}}_{n,n,k}^H{\mathbf{w}}_{n,k}}{\sum _{(j,i)}{|{\mathbf{h}}_{j,n,k}^H{\mathbf{w}}_{j,i}|}^2+{\sigma }_{n,k}^2}$

Transformed Problem
max ⁡ { w n , k } f q ( W , U , V ) s . t . p ˉ n − ∑ k = 1 K w n , k H w n , k ≥ 0 , ∀ n = 1 , … , N , \begin{array}{l} \mathop {\max }\limits_{\left\{ {{{\bf{w}}_{n,k}}} \right\}} \;\;{f_q}\left( {{\bf{W}},{\bf{U}},{\bf{V}}} \right)\\ {\rm{s}}.{\rm{t}}.\;{{\bar p}_n} - \sum\limits_{k = 1}^K {{\bf{w}}_{n,k}^H{{\bf{w}}_{n,k}}} \ge 0,\forall n = 1, \ldots ,N, \end{array} {wn,k​}max​fq​(W,U,V)s.t.pˉ​n​−k=1∑K​wn,kH​wn,k​≥0,∀n=1,…,N,​

the Lagrangian function

$L(\mathbf{W},\mathbf{U},\mathbf{V},\mathbf{\eta })=f_q(\mathbf{W},\mathbf{U},\mathbf{V})+\sum _{n=1}^N{\eta }_n\left({\bar{p}}_n-\sum _{k=1}^K{\mathbf{w}}_{n,k}^H{\mathbf{w}}_{n,k}\right)$

the Lagrange dual function: maximizing the Lagrangian

g ( η ) = m a x { w n , k } L ( W , U , V , η ) g\left( {\bm{\eta}} \right) = \mathop {{\rm{max}}}\limits_{\left\{ {{{\bf{w}}_{n,k}}} \right\}} \;L({\bf{W}},{\bf{U}},{\bf{V}},{\bm{\eta}}) g(η)={wn,k​}max​L(W,U,V,η)
$\frac{\partial }{\partial {\mathbf{w}}_{n,k}}L(\mathbf{W},\mathbf{U},\mathbf{V},\mathbf{\eta })=0\Rightarrow$
${\mathbf{w}}_{n,k}^{\ast }=\frac{\sqrt{(1+u_{n,k})}{\mathbf{h}}_{n,n,k}{v}_{n,k}}{\sum _{(m,l)}\left({\mathbf{h}}_{n,m,l}{v}_{m,l}{v}_{m,l}^H{\mathbf{h}}_{n,m,l}^H\right)+{\eta }_{n}I}$

the Lagrange dual problem: minimizing the Lagrange dual function

Lagrange multipliers are component-wise non-negative
$\underset{\mathbf{\eta }\ge 0}{\min }g\left(\mathbf{\eta }\right)$

Closed-Form FP

初始化${\mathbf{w}}_{n,k},\forall n,k$
重复

1. 更新$u_{n,k}^{\star }={\gamma }_{n,k}=\frac{{|{\mathbf{h}}_{n,n,k}^H{\mathbf{w}}_{n,k}|}^2}{\sum _{(j,i)\ne (n,k)}{|{\mathbf{h}}_{j,n,k}^H{\mathbf{w}}_{j,i}|}^2+{\sigma }_{n,k}^2}\in {\mathbb{R}}^1$ with ${\mathbf{w}}_{n,k},\forall n,k$
2. 更新$v_{n,k}^{\star }=\frac{\sqrt{(1+u_{n,k})}{\mathbf{h}}_{n,n,k}^H{\mathbf{w}}_{n,k}}{\sum _{(j,i)}{|{\mathbf{h}}_{j,n,k}^H{\mathbf{w}}_{j,i}|}^2+{\sigma }_{n,k}^2}$ with ${\mathbf{w}}_{n,k},\forall n,k$ and $u_{n,k},\forall n,k$
3. 更新${\eta }_n,\forall n$。利用二分法可以找到最小的${\eta }_n$ ，使得$\sum _{k=1}^K{\mathbf{w}}_{n,k}^H\left({\eta }_n\right){\mathbf{w}}_{n,k}\left({\eta }_n\right)={\bar{p}}_n$ 。
   其中，${\mathbf{w}}_{n,k}\left({\eta }_n\right)=\frac{\sqrt{(1+u_{n,k})}{\mathbf{h}}_{n,n,k}{v}_{n,k}}{\sum _{(m,l)}\left({\mathbf{h}}_{n,m,l}{v}_{m,l}{v}_{m,l}^H{\mathbf{h}}_{n,m,l}^H\right)+{\eta }_{n}I}$
4. 更新${\mathbf{w}}_{n,k}^{\ast }=\frac{\sqrt{(1+u_{n,k})}{\mathbf{h}}_{n,n,k}{v}_{n,k}}{\sum _{(m,l)}\left({\mathbf{h}}_{n,m,l}{v}_{m,l}{v}_{m,l}^H{\mathbf{h}}_{n,m,l}^H\right)+{\eta }_{n}I}$ with $u_{n,k},\forall n,k$, $v_{n,k},\forall n,k$, and ${\eta }_n,\forall n$

直到$f_q\left(\mathbf{W},\mathbf{U},\mathbf{V}\right)$收敛

对偶变量或Lagrange multipliers的更新：KKT条件 ${\eta }_n\left({\bar{p}}_n-\sum _{k=1}^K{\mathbf{w}}_{n,k}^H{\mathbf{w}}_{n,k}\right)=0,\forall n=1,\dots ,N,$
$\sum _{k=1}^K{\mathbf{w}}_{n,k}^H\left({\eta }_n\right){\mathbf{w}}_{n,k}\left({\eta }_n\right)$是关于${\eta }_n$的单调递减函数，利用二分法可以找到最小的${\eta }_n$ ，使得$\sum _{k=1}^K{\mathbf{w}}_{n,k}^H\left({\eta }_n\right){\mathbf{w}}_{n,k}\left({\eta }_n\right)={\bar{p}}_n$ ：
当 ${\eta }_n<{\eta }_n^{\ast }$时，$\sum _{k=1}^K{\mathbf{w}}_{n,k}^H\left({\eta }_n\right){\mathbf{w}}_{n,k}\left({\eta }_n\right)$ >基站最大发射功率${\bar{p}}_n$ 。
当${\eta }_n={\eta }_n^{\ast }$ 时，$\sum _{k=1}^K{\mathbf{w}}_{n,k}^H\left({\eta }_n\right){\mathbf{w}}_{n,k}\left({\eta }_n\right)$ =基站最大发射功率${\bar{p}}_n$ 。
当 ${\eta }_n>{\eta }_n^{\ast }$时，$\sum _{k=1}^K{\mathbf{w}}_{n,k}^H\left({\eta }_n\right){\mathbf{w}}_{n,k}\left({\eta }_n\right)$ <基站最大发射功率${\bar{p}}_n$ 。

Weighted MMSE

$u_{n,k}=\frac{{\mathbf{h}}_{n,n,k}^H{\mathbf{w}}_{n,k}}{\sum _{(m,j)}{|{\mathbf{h}}_{m,n,k}^H{\mathbf{w}}_{m,j}|}^2+{\sigma }_{n,k}^2}$
（图中h的下标打错了）

hm,n,k denote the downlink channel between BS m and UE k in cell n
wn,k denote the beamformer for UE k in cell n
the optimum Lagrange multiplier ${\mu }_n^{\star }$ can be determined efficiently by a bisection search method.

原论文

Q. Shi, M. Razaviyayn, Z. -Q. Luo and C. He, “An Iteratively Weighted MMSE Approach to Distributed Sum-Utility Maximization for a MIMO Interfering Broadcast Channel,” in IEEE Transactions on Signal Processing, vol. 59, no. 9, pp. 4331-4340, Sept. 2011, doi: 10.1109/TSP.2011.2147784.

${\mathbf{V}}_{i_k}$ 表示基站k对用户$i_k$ 的波束成形
${\mathbf{H}}_{i_k,j}$ 表示从基站j到用户 $i_k$的信道
$u_{k,i}=\frac{{\mathbf{h}}_{k,k,i}^H{\mathbf{w}}_{k,i}}{\sum _{(j,l)}{|{\mathbf{h}}_{j,k,i}^H{\mathbf{w}}_{j,l}|}^2+{\sigma }_{k,i}^2}$

Lagrange dual

上海交通大学 CS257 Linear and Convex Optimization
南京大学 Duality (I) - NJU

the standard form (5.1)

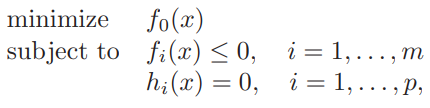
$\begin{array}{l}{\min }_{\mathbf{X}}f\left(\mathbf{X}\right)\\ \mathrm{s}.\mathrm{t}.g_i\left(\mathbf{X}\right)\le 0,\forall i=1,\dots ,m,\end{array}$

5.1.1 The Lagrangian

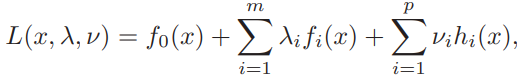
the dual variables or Lagrange multiplier vectors associated with the problem (5.1).

5.1.2 The Lagrange dual function

the minimum value of the Lagrangian

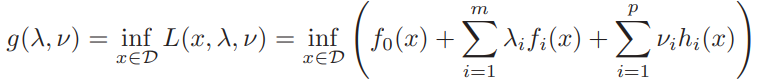
5.2 The Lagrange dual problem

the Lagrange dual problem associated with the problem (5.1).

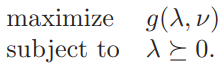
5.2.3 Strong duality and Slater’s constraint qualification

5.2.3 Strong duality and Slater’s constraint qualification

Slater’s theorem states that
strong duality holds, if Slater’s condition holds (and the problem is convex).
strong duality obtains, when the primal problem is convex and Slater’s condition holds

Slater’s Condition for Convex Problems
上海交通大学 CS257 Linear and Convex Optimization

5.5.3 KKT optimality conditions

Karush-Kuhn-Tucker (KKT) conditions

for any optimization problem with differentiable objective and constraint functions for which strong duality obtains, any pair of primal and dual optimal points must satisfy the KKT conditions (5.49).

仿真