1.关于那个整形存储入char的

是先取好补码,再截断

例:

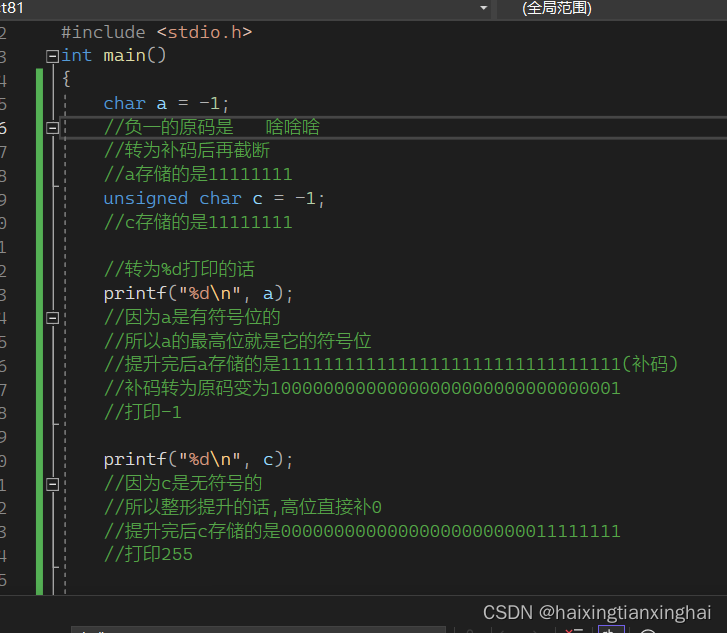
2.%u是以十进制的形式打印无符号整数

3.注意(背):存储的char类型变量的补码为10000000的直接解析为-128

4.signed char 类型的变量取值范围是-128~127

5.unsigned char 类型的变量取值范围是0~255

6.有符号类型的变量发生整形提升时,是按照它自己的最高位进行整形提升,而后才会选择去打印(即而后才看打印的   %?   对它的影响)

7.自己悟:

图12345678搜

8.观摩:

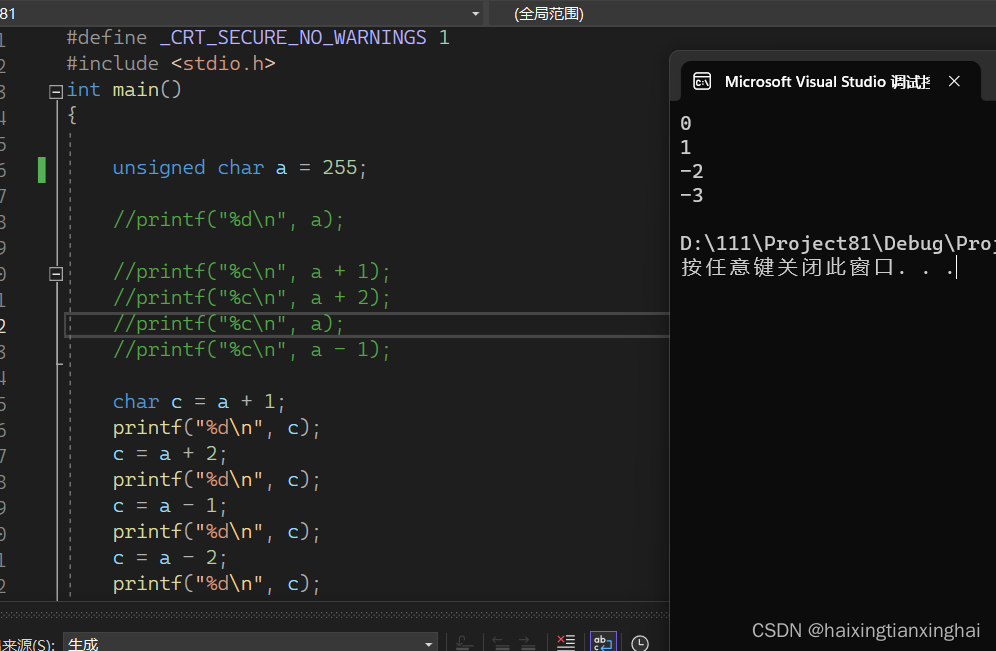
和

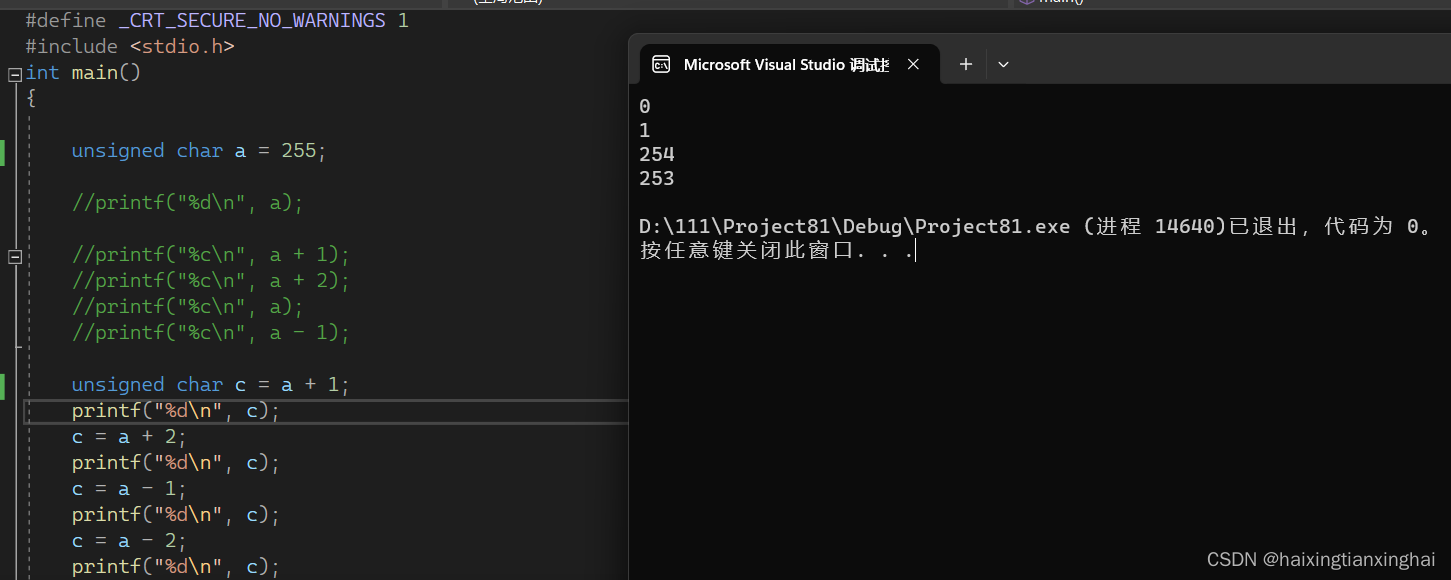
总之,注意好那个无符号以及截断的特别

9.在小端环境下,int   的   1   计入内存中是   (十六进制表示)   (低地址)   01 00 00 00   (高地址)   ,   (低地址)   02是02 00 00 00   (高地址)

10.1E12表示的是1乘以10的12次方(已测过)

11.任意一个浮点数可以表示为这样的形式搜:

(数)V=(-1)^s*M*2^E
(-1)^s表示符号位，当S=0，V为正数;当S=1，V为负数
M 表示有效数字，M大于等于1且小于2
2^E表示指数位

12.将十进制的一个数字换位为二进制

例:

5.5换为101.1(前换前,后换后)

二进制的101.1可以用科学计数法化为1.011*2^2,根据国际标准,可以表示为:

(-1)^0 * 1.011 * 2^2

但是对于另一个例子:3.14,人为来配可能很难配

13.而十进制转二进制另另一个例题搜

14.对于float类型的和double类型的存储方式的不完全相同搜:

15.存储浮点型数据:在存储M时,默认这个数的第一位总是1，因此可以被舍去，只保存后面的XXXXXX部分。比如说保存1.01的时候，只保存后边的01，等到读取的时候，再把第一位的1加上去。这样做的目的是节省1位有效数字。以32位浮点数为例，留给M只有23位，而将第一位的1舍去以后，等于可以保存24位有效数字。

存储E时,因为E为一个无符号整数(unsigned int),那么如果E为8位，它的取值范围就为0~255;如果E为11位，它的取值范围就是0~2047。但科学计数法中的E是可以为负数的，所以IEEE 754规定存入内存时E的真实值必须再加上一个中间数，对于8位的E这个中间数是  127  ;对于11位的E，这个中间数是  1023  。比如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001。

所以5.5的二进制序列就是:0   10000001 01100000000000000000000(1   8   23位)(不够的话补零)

//还原是还原为1.01100000000000000000000(1   23   位)

而0100 0000 1011 0000 0000 0000 0000 0000

换为16进制:40 B0 00 00(在内存中如果是小端存储则显示为00 00 b0 40)

16.浮点型从内存中的取出搜:

大概知道下浮点型的存储和取出即可

17.关于浮点型的存储和取出和整数的存储和取出转化的一个例题搜:

18.有些浮点数在内存中无法精确保存

19.正确比较浮点数的方式搜:

20.