Motion Plan之搜索算法笔记
Motion Plan之基于采样的路径规划算法笔记
Motion Plan之带动力学约束路径搜索

Motion Plan之轨迹生成笔记
文章开始前先回顾下上次的带约束的轨迹生成，轨迹生成本质就是曲线拟合。曲线拟合常用的方法有：多项式、贝赛尔曲线、三次样条差值…下面的例子我们会选择多项式曲线拟合来做讲解。
有了曲线拟合的方法，理论就能够在通过高路径规划得到的wayponit点就能够生成一条可以通行的路径了。然而如果只是生成路径就有点粗糙了，生成路径是需要满足一些约束条件的，比如生成的路径轨迹整体要光滑、路径必须要经过某些指定点、不能碰到障碍物、连续性要求、考虑到移动机器人的物理限制（比如加速度小于20m/s）…
接着就是考虑了这么多约束求解如果太复杂也不行，太复杂了你就跑不快、太复杂了消耗能量大、太复杂了出了问题差问题很难。所以有没可能把上面约束问题都统一到一个求解框架、一步就求解完又成了科研人员研究新方向。

多项式轨迹拟合

由于四旋翼无人机以及双轮差速轮机器人(不准确的简化)，它们轨迹在各个坐标轴上是独立的，因此我们可以对其分别进行轨迹拟合。也就是说我们可以分别对它们在x , y , z x,y,zx,y,z轴上进行路径生成，然后直接将三个轴合成就可以得到一个完整的空间轨迹。
因此后续算法细节介绍中，将不再强调轨迹是一维、二维还是三维，均以一维来进行介绍，可以很容易将其推广到任意维度。

五次多项式曲线表示

$P(t)=p_5{t}^5+p_4{t}^4+p_3{t}^3+p_2{t}^2+p_{1}t+p_0$
进行一阶求导，相当于得到了它的速度函数：
$\frac{dP(t)}{dt}=[p_5,p_4,p_3,p_2,p_1,p_0]\left[\begin{array}{c}5t^4\\ 4t^3\\ 3t^2\\ 2t^1\\ t^0\\ 1\end{array}\right]$

其进行二阶求导，相当于得到的了它的加速度函数：
$\frac{d^{2}P(t)}{dt}=[p_5,p_4,p_3,p_2,p_1,p_0]\left[\begin{array}{c}5\ast 4t^3\\ 4\ast 2t^2\\ 3\ast 2t^1\\ 2\ast 1t^0\\ 0\ast 1\\ 0\end{array}\right]$
三阶求导，得到Jerk函数：
$\frac{d^{3}P(t)}{dt}=[p_5,p_4,p_3,p_2,p_1,p_0]\left[\begin{array}{c}5\ast 4\ast 3t^2\\ 4\ast 3\ast 2t^1\\ 3\ast 2\ast 1t^0\\ 2\ast 1\ast 0\\ 0\ast 1\ast 0\\ 0\ast 0\end{array}\right]$
四阶求导，则得到了Snap函数:
$\frac{d^{4}P(t)}{dt}=[p_5,p_4,p_3,p_2,p_1,p_0]\left[\begin{array}{c}5\ast 4\ast 3\ast 2t^1\\ 4\ast 3\ast 2\ast 1t^0\\ 3\ast 2\ast 1\ast 0\\ 2\ast 1\ast 0\ast 0\\ 0\ast 1\ast 0\ast 0\\ 0\ast 0\ast 0\ast 0\end{array}\right]$

求解

轨迹的表达只与时间$t$有关，也就是说我们如果知道机器人的起始点位置、位置的一阶倒数（速度），二阶倒数（加速度）和终止位置、位置的一阶倒数（速度），二阶倒数（加速度）方程的参数$[p_5,p_4,p_3,p_2,p_1,p_0]$可以求解出来。那么这段轨迹拟合就能够表示出来了。下面给一个例子来说明。

	位置	速度	加速度
t=0	a	v0	0
t=T	b	vT	0

求解：
$\left[\begin{array}{c}a\\ v_0\\ 0\\ b\\ v_T\\ 0\end{array}\right]=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 2& 0& 0& 0\\ 1& T& T^2& T^3& T^4& T^5\\ 0& 1& T^1& 3T^2& 4T^3& 5T^4\\ 0& 0& 2& 6T^1& 12T^2& 20T^3\end{array}\right]\left[\begin{array}{c}{p}_5\\ p_4\\ p_3\\ p_2\\ p_1\\ p_0\end{array}\right],d=A_F(T)P$

对应代码实现

import numpy as np
import matplotlib.pyplot as plt# degrees to radian converter
def deg_to_rad(T):return (T/180)*np.piqi = float(input('qi = ')) # initial position                0, for testing
qi = deg_to_rad(qi)vi = float(input('vi = ')) # initial velocity                0, for testing     
vi = deg_to_rad(vi)aci = float(input('aci = ')) # initial acceleration          0, for testing
aci = deg_to_rad(aci)qf = float(input('qf = ')) # final position                  90, for testing
qf = deg_to_rad(qf)vf = float(input('vf = ')) # final velocity                  50, for testing
vf = deg_to_rad(vf)acf = float(input('acf = ')) # final acceleration            60, for testing
acf = deg_to_rad(acf)ti = float(input('ti = ')) # initial time                   0, for testing
tf = float(input('tf = ')) # final time                     9, for testing## Quintic Polynomial
## Solve the solution for q(t)=c0+c1*t+c2*t**2+c3*t**3+c4*t**4+c5*t**5#这个对应的就是上面的AF(t)矩阵
M = [[1, ti, ti**2, ti**3, ti**4, ti**5],[0, 1, 2*ti, 3*ti**2, 4*ti**3, 5*ti**4],[0, 0, 2, 6*ti, 12*ti**2, 20*ti**3],[1, tf, tf**2, tf**3, tf**4, tf**5],[0, 1, 2*tf, 3*tf**2, 4*tf**3, 5*tf**4],[0, 0, 2, 6*tf, 12*tf**2, 20*tf**3]]  M = np.matrix(M)   b = [[qi], [vi], [aci], [qf], [vf], [acf]]a = np.linalg.inv(M) * b  #这个就是上面的p参数向量x = np.arange(ti,tf,0.05)def qt(t,c0,c1,c2,c3,c4,c5):return c0 + c1*t + c2*t**2 + c3*t**3 + c4*t**4 + c5*t**5y = qt(x,a[0,0],a[1,0],a[2,0],a[3,0],a[4,0],a[5,0])
print(a)plt.figure()
plt.plot(x,y,'r',linestyle='-')
plt.text(1,1.5,'P(t)=p0+p1*t+p2*t**2+p3*t**3+p4*t**4+p5*t**5')
plt.grid(True)
plt.show()

带约束的轨迹拟合

上面已经给出了两个点之间用5次多项式来拟合出一条轨迹的方法，然而一条轨迹肯定不会是只给两个点（起止点）中间还有很多的waypoint作为轨迹的锚定点。如果用上面的方法似乎是没法解决给定多个点来确定一条轨迹的。那么该如何解决呢，你可能会讲那还不简单直接把给定的多个点变成两个点的组合list，然后没两个点生成一段轨迹最后把所有段兜起来不就是一条能够把给定的多个点都穿过去的轨迹了吗。
看起来似乎是没什么问题的，实际我们也是如此来做的。但是这样生成的轨迹往往就是没有考虑到机器人物理约束的，并且行驶性能不太好。那么我们要如何把机器人的物理性和驾驶性都考虑进来呢。这边用的是轨迹的自身特性：最小化snap、jerk保证光滑性来保证驾驶性和物理性；必须要要通过给定点，衔接点上位置、速度、加速度必须相等（上一段的结束点就是下一段结束点）；不碰到障碍物转变成轨迹要在可行区域范围内，转成范围不等式约束。

代价函数

构建了一个如下的代价含数$J_m$，对应的是一段多项式轨迹的四阶导数(Snap)平方的积分。两个向量相乘为常数，那么它们乘积等于它们乘积的转置。
$$\begin{gathered} J_m={\int }_{T_{m-1}}^{T_m}(\frac{d^{4}P(t)}{d{t}^4}{)}^2 \\ {\int }_{T_{m-1}}^{T_m}{\left[\begin{array}{c}{p}_5\\ p_4\\ p_3\\ p_2\\ p_1\\ p_0\end{array}\right]}^T\left[\begin{array}{c}5\ast 4\ast 3\ast 2t^1\\ 4\ast 3\ast 2\ast 1t^0\\ 3\ast 2\ast 1\ast 0\\ 2\ast 1\ast 0\ast 0\\ 0\ast 1\ast 0\ast 0\\ 0\ast 0\ast 0\ast 0\end{array}\right]{\left[\begin{array}{c}5\ast 4\ast 3\ast 2t^1\\ 4\ast 3\ast 2\ast 1t^0\\ 3\ast 2\ast 1\ast 0\\ 2\ast 1\ast 0\ast 0\\ 0\ast 1\ast 0\ast 0\\ 0\ast 0\ast 0\ast 0\end{array}\right]}^T\left[\begin{array}{c}{p}_5\\ p_4\\ p_3\\ p_2\\ p_1\\ p_0\end{array}\right] \\ =P_m^T{Q}_m{P}_m \\ \Rightarrow Q=\left[\begin{array}{c}5\ast 4\ast 3\ast 2t^1\\ 4\ast 3\ast 2\ast 1t^0\\ 3\ast 2\ast 1\ast 0\\ 2\ast 1\ast 0\ast 0\\ 0\ast 1\ast 0\ast 0\\ 0\ast 0\ast 0\ast 0\end{array}\right]{\left[\begin{array}{c}5\ast 4\ast 3\ast 2t^1\\ 4\ast 3\ast 2\ast 1t^0\\ 3\ast 2\ast 1\ast 0\\ 2\ast 1\ast 0\ast 0\\ 0\ast 1\ast 0\ast 0\\ 0\ast 0\ast 0\ast 0\end{array}\right]}^T\Rightarrow Q=\left[\begin{array}{cccccc}14400& 2880& 0& 0& 0& 0\\ 2880& 576& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right] \end{gathered}$$
上面是一段曲线拟合的代价函数，如果有M段轨迹，那么每一段轨迹都是一个高阶的多项式函数，写出代价函数和如下：
$$\begin{gathered} J=J_0+J_1+J_2+...+J_M \\ ={\sum }_0^M{P}_m^T{Q}_m{P}_m \\ ={\left[\begin{array}{c}{P}_0\\ P_1\\ ⋮\\ P_M\end{array}\right]}^T\left[\begin{array}{ccccc}{Q}_0& 0& \dots & \dots & 0\\ 0& Q_1& 0& \dots & 0\\ ⋮& ⋮& ⋮& \dots & ⋮\\ 0& 0& \dots & 0& Q_M\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ ⋮\\ P_M\end{array}\right] \end{gathered}$$

约束条件表示

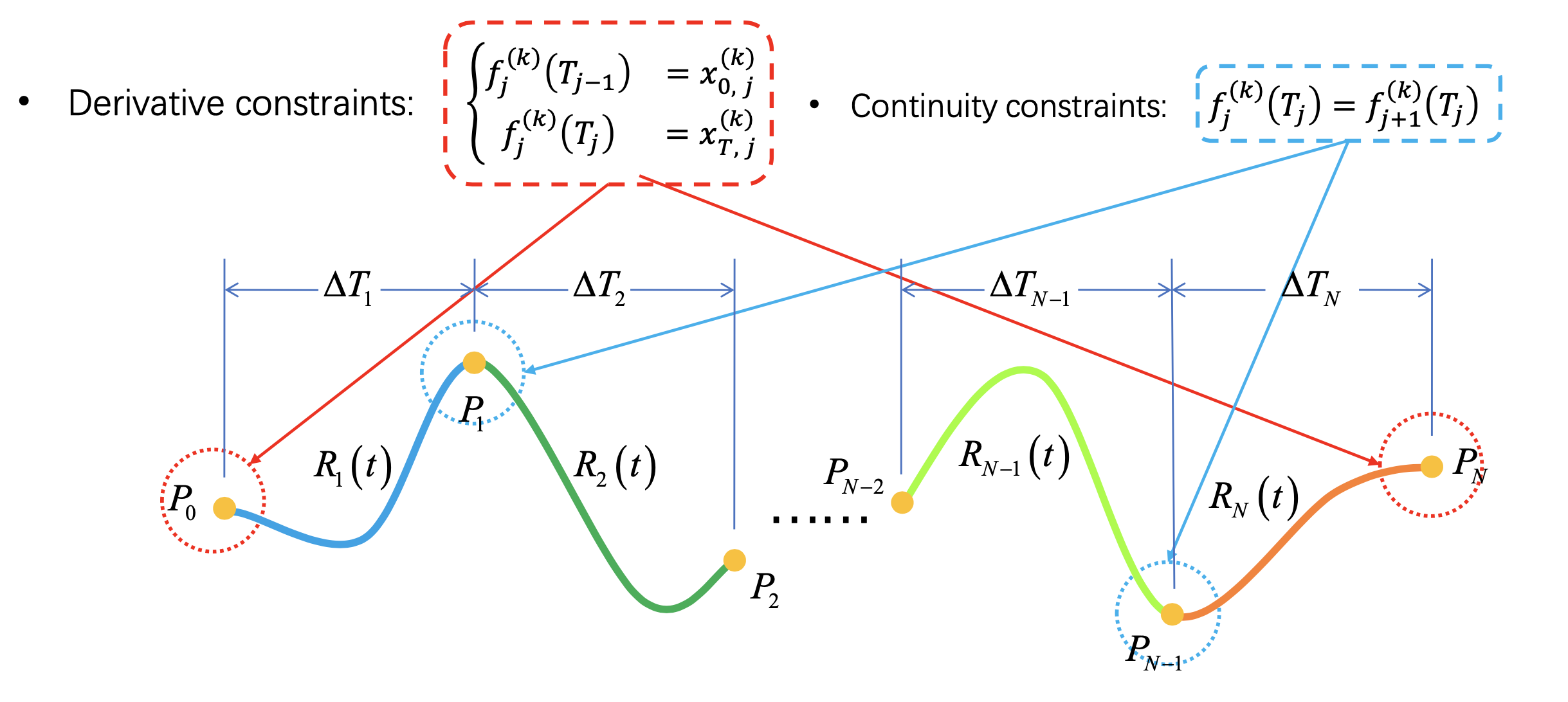
连续性约束

中间的航迹点在两段轨迹的接合处是左右两边状态要连续。如果要最小化的目标是Jerk，那么我们必须保证接合处三阶导数是连续的。因为我们要对Jerk进行积分，那么多项式在求导3次之后必须要连续，所以要确保0阶、1阶、2阶导数都是光滑的，也就是保证求导到加速度函数依然是光滑的，这一点就体现了多项式轨迹的优势，它天然就是一个高阶光滑的函数。
写成数学的形式，就是：
$P_m^k(T_m)=P_{m+1}^k(T_m)$
意思就是m段轨迹和m+1段轨迹，他们的k阶导数必须一致；推导如下：
$$\begin{gathered} P_m^k(T_m)=P_{m+1}^k(T_m) \\ \Rightarrow {\sum }_{i\ge k}\frac{i!}{(i-k)!}{T}_m^{i-k}{p}_{m,i}={\sum }_{l\ge k}\frac{l!}{(l-k)!}{T}_m^{l-k}{p}_{m+1,l} \\ \Rightarrow {\sum }_{i\ge k}\frac{i!}{(i-k)!}{T}_m^{i-k}{p}_{m,i}-{\sum }_{l\ge k}\frac{l!}{(l-k)!}{T}_m^{l-k}{p}_{m+1,l}=0 \\ \Rightarrow [A_m-A_{m+1}]\left[\begin{array}{c}{P}_m\\ P_m+1\end{array}\right]=0 \end{gathered}$$

微分约束

大多数情况下，对轨迹的位置有一些限制的，并不能随意生成，所以还需要给中间的航迹点加一些限制。限制轨迹必须通过某一些点，或者以一个确定的状态通过某一些中间的航迹点。也就是上述的这些多项式系数中，有一些是已知的。包括位置、速度、加速度、Jerk、Snap等等的限制。
机器人的终点速度和加速度也是可以事先给定的。机器人中间航迹点的位置也是需要事先给定的，但是机器人中间点的速度和加速度等信息，我们没法去约束它，因为很难去确定机器人到达某一个点的速度或者加速度，所以对于中间点的速度和加速度，或者更高阶的Jerk甚至Snap等，不对其进行微分限制，让它们只具有连续性约束，然后让优化器给它们分配最优的状态。
那么用数学方法去表述上面的内容，如下：
起始点和终点的位置、速度、加速度等使用确定值限制：
P_0(0) = 确定值 \rightarrow 起始点位置\
P_0^{(1)}(0) = 确定值 \rightarrow 起始点速度\
P_0^{(2)}(0) = 确定值 \rightarrow 起始点加速度\
P_M(T_m) = 确定值 \rightarrow 终止点位置\
P_M^{(T_m)}(0) = 确定值 \rightarrow 终止点速度\
P_M^{(T_m)}(0) = 确定值 \rightarrow 终止点加速度\$<br/>中间必须穿过的轨迹点：<br/>$P_0(T_0) = 确定值 \rightarrow 第0段轨迹中T_0时刻必须经过点位置\
P_1(T_0) = 确定值 \rightarrow 第1段轨迹中T_0时刻必须经过点位置\
P_1(T_m) = 确定值 \rightarrow 第1段轨迹中T_m时刻必须经过点位置
把上面的过程写成数学等式(以任意一段多项式轨迹为例)：$$\begin{gathered} \left[\begin{array}{cccc}{T}_{m-1}^N& T_{m-1}^{N-1}& \dots & T_{m-1}^0\\ T_m^N& T_m^{N-1}& \dots & T_m^0\\ N{T}_{m-1}^{N-1}& T_{m-1}^{N-2}& \dots & 0\\ ⋮& ⋮& ⋮& ⋮\\ \dots & \frac{i!}{(i-k)!}{T}_{m-1}^{i-k}& \dots & \dots \\ \dots & \frac{i!}{(i-k)!}{T}_m^{i-k}& \dots & \dots \end{array}\right]\left[\begin{array}{c}{P}_N\\ P_{N-1}\\ ⋮\\ P_0\end{array}\right]=\left[\begin{array}{c}{p}_{T_{m-1}}\\ p_{T_m}\\ v_{T_{m-1}}\\ v_{T_m}\\ \alpha T_{m-1}\\ \alpha T_m\\ ⋮\end{array}\right] \\ \Rightarrow A_m{P}_m=d_m \end{gathered}$$
以上就是对一段轨迹的头和尾进行微分限制，对于中间的航迹点。通常做法，对于它们高于0阶之后的导数不进行微分限制。
如果将连续性约束和微分约束进行合并(下面是多段轨迹），则可以得到如下式子：
$\left[\begin{array}{cccccc}{A}_0& 0& 0& 0& \dots & 0\\ A_0& -A_1& 0& 0& \dots & 0\\ 0& A_1& -A_2& 0& \dots & 0\\ 0& A_1& 0& 0& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& \dots & A_M\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\\ ⋮\\ P_M\end{array}\right]=\left[\begin{array}{c}{d}_0\\ 0\\ d_1\\ 0\\ ⋮\\ d_M\end{array}\right]$
构建了一个带约束的QP问题
$$\begin{gathered} min{\left[\begin{array}{c}{P}_0\\ P_1\\ ⋮\\ P_M\end{array}\right]}^T\left[\begin{array}{ccccc}{Q}_0& 0& \dots & \dots & 0\\ 0& Q_1& 0& \dots & 0\\ ⋮& ⋮& ⋮& \dots & ⋮\\ 0& 0& \dots & 0& Q_M\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ ⋮\\ P_M\end{array}\right]=P^{T}QP \\ s.t.\left[\begin{array}{cccccc}{A}_0& 0& 0& 0& \dots & 0\\ A_0& -A_1& 0& 0& \dots & 0\\ 0& A_1& -A_2& 0& \dots & 0\\ 0& A_1& 0& 0& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& \dots & A_M\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ P_2\\ P_3\\ ⋮\\ P_M\end{array}\right]=\left[\begin{array}{c}{d}_0\\ 0\\ d_1\\ 0\\ ⋮\\ d_M\end{array}\right] \end{gathered}$$
到这边QP问题已经构建好了，接下来用QP求解库来求解就行了，可以求到一个全局最优解。

闭式求解

虽然上述方法在单个段和小联合优化问题中效果良好，但在涉及多个段、高阶多项式和时间变化范围广泛的情况下，该公式求解条件恶劣。因此，它仅适用于短轨迹，并且必须改进以在优化需要许多路径点和段的长距离路径时变得实用。
我们通过使用替代技术将问题转化为无约束的二次规划，并直接求解端点导数作为决策变量来改进上述解决方案。实际上，我们的重构比上述方法稳定得多，允许在单个矩阵操作中联合优化超过50个多项式段而不会遇到数值问题。一旦找到最优路径点导数，就可以通过反转适当的约束矩阵获得连接每对路径点的最小阶多项式。
总一句话就是上面已经得到了QP问题，可以进行求解了。然而如果硬求解速度不快，并且不容易求解。那么是否可以把上面的QP问题整合成一个无约束的QP问题。

$$\begin{gathered} \left[\begin{array}{c}P(0)\\ P^{(1)}(0)\\ P^{(2)}(0)\\ P(T)\\ P^{(1)}(T)\\ P^{(2)}(T)\end{array}\right]=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 2& 0& 0& 0\\ 1& T& T^2& T^3& T^4& T^5\\ 0& 1& T^1& 3T^2& 4T^3& 5T^4\\ 0& 0& 2& 6T^1& 12T^2& 20T^3\end{array}\right]\left[\begin{array}{c}{p}_5\\ p_4\\ p_3\\ p_2\\ p_1\\ p_0\end{array}\right], \\ \Rightarrow d_m=A_m{P}_m \\ {P}_m=A_m^{-1}{d}_m \end{gathered}$$
代价函数中的系数向量通过映射矩阵$A_m^{-1}{d}_m$进行替换，则得到下式：
$$\begin{gathered} min{\left[\begin{array}{c}{P}_0\\ P_1\\ ⋮\\ P_M\end{array}\right]}^T\left[\begin{array}{ccccc}{Q}_0& 0& \dots & \dots & 0\\ 0& Q_1& 0& \dots & 0\\ ⋮& ⋮& ⋮& \dots & ⋮\\ 0& 0& \dots & 0& Q_M\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ ⋮\\ P_M\end{array}\right] \\ {\left[\begin{array}{c}{d}_0\\ d_1\\ ⋮\\ d_m\end{array}\right]}^T{\left[\begin{array}{ccccc}{A}_0& 0& \dots & \dots & 0\\ 0& A_1& \dots & \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & A_M\end{array}\right]}^{-T}\left[\begin{array}{ccccc}{Q}_0& 0& \dots & \dots & 0\\ 0& Q_1& 0& \dots & 0\\ ⋮& ⋮& ⋮& \dots & ⋮\\ 0& 0& \dots & 0& Q_M\end{array}\right]{\left[\begin{array}{ccccc}{A}_0& 0& \dots & \dots & 0\\ 0& A_1& \dots & \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & A_M\end{array}\right]}^{-1}\left[\begin{array}{c}{d}_0\\ d_1\\ ⋮\\ d_m\end{array}\right] \\ \Rightarrow min{d}^T{A}^{-T}{A}^{-1}d \end{gathered}$$
上式实际上已经通过$A_m^{-1}{d}_m$进行替换把微分约束给带入到了代价函数中。$d_m$对应的就是起始、终止、中间点的具体位置、速度、加速度值；上面的代价函数是多段轨迹的代价函数，也就是每个$d_m$包含的是一段轨迹必须包含的的中间点、起始点、终止点确定值。但是连续性约束还没有引入到代价函数中。我们来看看连续性约束是如何定义和用数学式来表达的。

‘’‘中间的航迹点在两段轨迹的接合处是左右两边状态要连续。如果要最小化的目标是Jerk，那么我们必须保证接合处三阶导数是连续的。因为我们要对Jerk进行积分，那么多项式在求导3次之后必须要连续，所以要确保0阶、1阶、2阶导数都是光滑的，也就是保证求导到加速度函数依然是光滑的，这一点就体现了多项式轨迹的优势，它天然就是一个高阶光滑的函数。
写成数学的形式，就是：
$P_m^k(T_m)=P_{m+1}^k(T_m)$ ‘’’

也就是说连续性表示的是相邻的两段轨迹之间的关系。也就是有连续约束的两段轨迹，两段的轨迹结合处的三阶导数必须要一样，等价于前段结尾和后段开始这三阶导数表达式可以省掉一个表达。那么我， 引入C来将连续性约束进行引入到代价函数中。**C矩阵本身是一个只包含0和1的矩阵，它的作用就是给所有[ d 0 d 1 ⋯ d M ] 进行一个组合，**将固定的变量放在头部，将需要就行优化的变量方位尾部，并且对于连续性约束的变量，由于他们的值是相等的，因此选择其中一个来表达连续性约束。（这是一个很巧妙方法，经过段之间组合排序就能够把连续约束引入进来，把带约束优化求解变成无约束优化求解）。

$$\begin{gathered} \left[\begin{array}{c}{d}_{m_F}\left(\begin{array}{c}{d}_{0,0}^{(0)}\\ d_{0,0}^{(1)}\\ d_{0,0}^{(2)}\\ d_{T,0}^{(0)}\\ d_{T,0}^{(1)}\\ d_{T,0}^{(2)}\\ d_{T,1}^{(0)}\\ d_{T,1}^{(1)}\\ d_{T,1}^{(2)}\end{array}\right)\\ d_{m_P}\left(\begin{array}{c}{d}_{0,1}^{(0)}\\ d_{0,1}^{(1)}\\ d_{0,1}^{(2)}\end{array}\right)\end{array}\right]=\left[\begin{array}{ccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{d}_{0,0}^{(0)}\\ d_{0,0}^{(1)}\\ d_{0,0}^{(2)}\\ d_{T,0}^{(0)}\\ d_{T,0}^{(1)}\\ d_{T,0}^{(2)}\\ d_{T,1}^{(0)}\\ d_{T,1}^{(1)}\\ d_{T,1}^{(2)}\end{array}\right] \\ \Rightarrow d_m=C^T\left[\begin{array}{c}{d}_{m_F}\\ d_{m_P}\end{array}\right] \end{gathered}$$
现在，这个新二次成本函数的决策变量是段的端点导数。我们重新排序这些变量，使得固定/指定的导数被分组在一起（$d_F$），而自由/未指定的导数被分组在一起（$d_P$）。使用由1和0组成的排列矩阵（C）来完成这种重新排序。现在我们有：
$J={\left[\begin{array}{c}{d}_F\\ d_P\end{array}\right]}^{T}C{A}^{-T}Q{A}^{-1}{C}^T\left[\begin{array}{c}{d}_F\\ d_P\end{array}\right]={\left[\begin{array}{c}{d}_F\\ d_P\end{array}\right]}^T\left[\begin{array}{cc}{R}_{FF}& R_{FP}\\ R_{PF}& R_{PP}\end{array}\right]\left[\begin{array}{c}{d}_F\\ d_P\end{array}\right]$
其中我们用 A 和 Q 来简化符号表示的分块对角矩阵。我们将新的增广成本矩阵组合成一个单独的矩阵 R，并根据固定和自由导数的索引对其进行分区。分区允许我们写出总成本的表达式：
$J=d_F^T{R}_{FF}{d}_F+d_F^T{R}_{FP}{d}_P+d_P^T{R}_{PF}{d}_F+d_P^T{R}_{PP}{d}_P$
对 J 进行微分并置零，得到自由导数的最优值向量，其中涉及固定/指定导数和成本矩阵：
对于上式我们要求的变量是$d_P$，因此将其对 求导，$d_P$并零导数为0时取极值点的值对应的就是最优的$d_P^{\ast }$
$$\begin{gathered} \frac{\partial J}{\partial d_p}=2d_F^T{R}_{FP}+2R_{PP}{d}_p=0 \\ \Rightarrow d_p^{\ast }=-R_{PP}^{-1}{R}_{FP}^T{d}_F \end{gathered}$$
求解出来了$d_P^{\ast }$之后，可以通过对将导数映射回系数空间的适当约束方程进行的各个评估来恢复多项式。只需要将它带入C 和M就能求出最终的各个多项式的系数：
$P=M^{-1}{C}^T\left[\begin{array}{c}{d}_F\\ d_P^{\ast }\end{array}\right]$

代码实现

带约束求解代码

Input：

import numpy as np
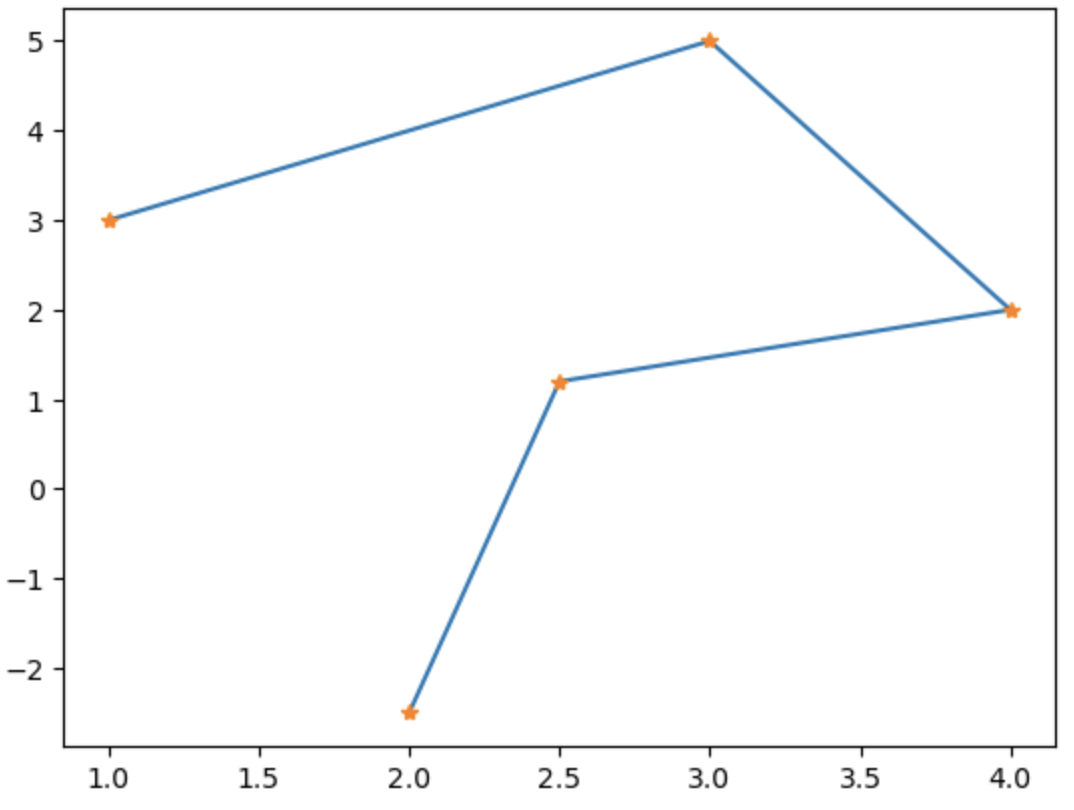
import matplotlib.pyplot as pltpath = [[1, 3], [3, 5], [4, 2], [2.5, 1.2], [2, -2.5]]
path = np.array(path)
plt.plot(path[:, 0], path[:, 1])
plt.plot(path[:, 0], path[:, 1], "*")
plt.show()

超参数设置：

#%% 一维轨迹优化
x = path[:, 0]
print(x)
# 分配时间
deltaT = 2 # 每一段2秒
T = np.linspace(0, deltaT * (len(x) - 1), len(x))K = 3                   # jerk为3阶导数，取K=3
n_order = 2 * K - 1     # 多项式阶数
M = len(x) - 1          # 轨迹的段数
N = M * (n_order + 1)   # 矩阵Q的维数

构建Q矩阵和代价函数：

'''
1.因为这个示例给的是minimum 3阶导数，所以每段轨迹的Qk的左上角都是0，矩阵参数设置从3行3列一下构建
2.因为每段轨迹的Qk矩阵是对角阵，所以把求一半另一半用转置赋值来实现
3.Q矩阵大小是M段*（几次多项式+1）的大小表示
4.Q是对角的分块阵列，在矩阵对角上有值其他地方都是0
'''
def getQk(T_down, T_up):Q = np.zeros((6, 6))Q[3][4] = 36 * (T_up**2 - T_down**2)Q[3][5] = 40 * (T_up**3 - T_down**3)Q[4][5] = 60 * (T_up**4 - T_down**4)Q = Q + Q.T # Q为对称矩阵Q[3][3] = 36 * (T_up**1 - T_down**1)Q[4][4] = 48 * (T_up**3 - T_down**3)Q[5][5] = 80 * (T_up**5 - T_down**5)return QQ = np.zeros((N, N))
for k in range(1, M + 1):Qk = getQk(T[k - 1], T[k])Q[(6 * (k - 1)) : (6 * k), (6 * (k - 1)) : (6 * k)] = QkQ = Q * 2 # 因为标准目标函数为： 1/2xTQx + qTx，所以要乘2

构建约束条件

########### 约束 ###########
# 1.导数约束 Derivative Constraint
A0 = np.zeros((2 * K + M - 1, N)) b0 = np.zeros(len(A0))# 添加首末状态约束(包括位置、速度、加速度)
for k in range(K): for i in range(k, 6):c = 1for j in range(k):c *= (i - j)A0[0 + k * 2][i]                = c * T[0]**(i - k)A0[1 + k * 2][(M - 1) * 6 + i]  = c * T[M]**(i - k)b0[0] = x[0]
b0[1] = x[M]
# 添加每段轨迹的初始位置约束
for m in range(1, M):for i in range(6):A0[6 + m - 1][m * 6 + i] = T[m]**ib0[6 + m - 1] = x[m]# 2.连续性约束 Continuity Constraint
A1 = np.zeros(((M - 1) * 3, N))
b1 = np.zeros(len(A1))
for m in range(M - 1):for k in range(3): # 最多两阶导数相等    for i in range(k, 6):c = 1for j in range(k):c *= (i - j)index = m * 3 + kA1[index][m * 6 + i] = c * T[m + 1]**(i - k)A1[index][(m + 1)* 6 + i] = -c * T[m + 1]**(i - k)A = np.vstack((A0, A1))
b = np.hstack((b0, b1))

带约束求解规划（用的cvxopt库）：
Cvxopt.solvers.qp(P,q,G,h,A,b)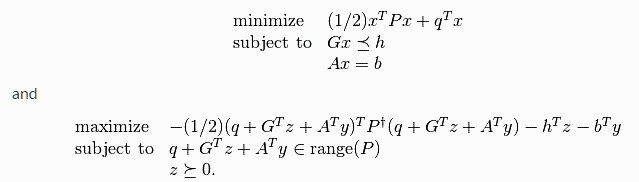

• P对应的代价函数矩阵
• q对应代价函数一阶向量
• G对应不等式矩阵
• h对应不等式的值条件
• A对应等式矩阵
• b对应等式的值条件

#%% 解二次规划问题
from cvxopt import matrix, solvers
# 目标函数
Q = matrix(Q)
q = matrix(np.zeros(N))
# 等式约束: Ax = b
A = matrix(A)
b = matrix(b)
result = solvers.qp(Q, q, A=A, b=b)
p_coff = np.asarray(result['x']).flatten()

一维求解可视化：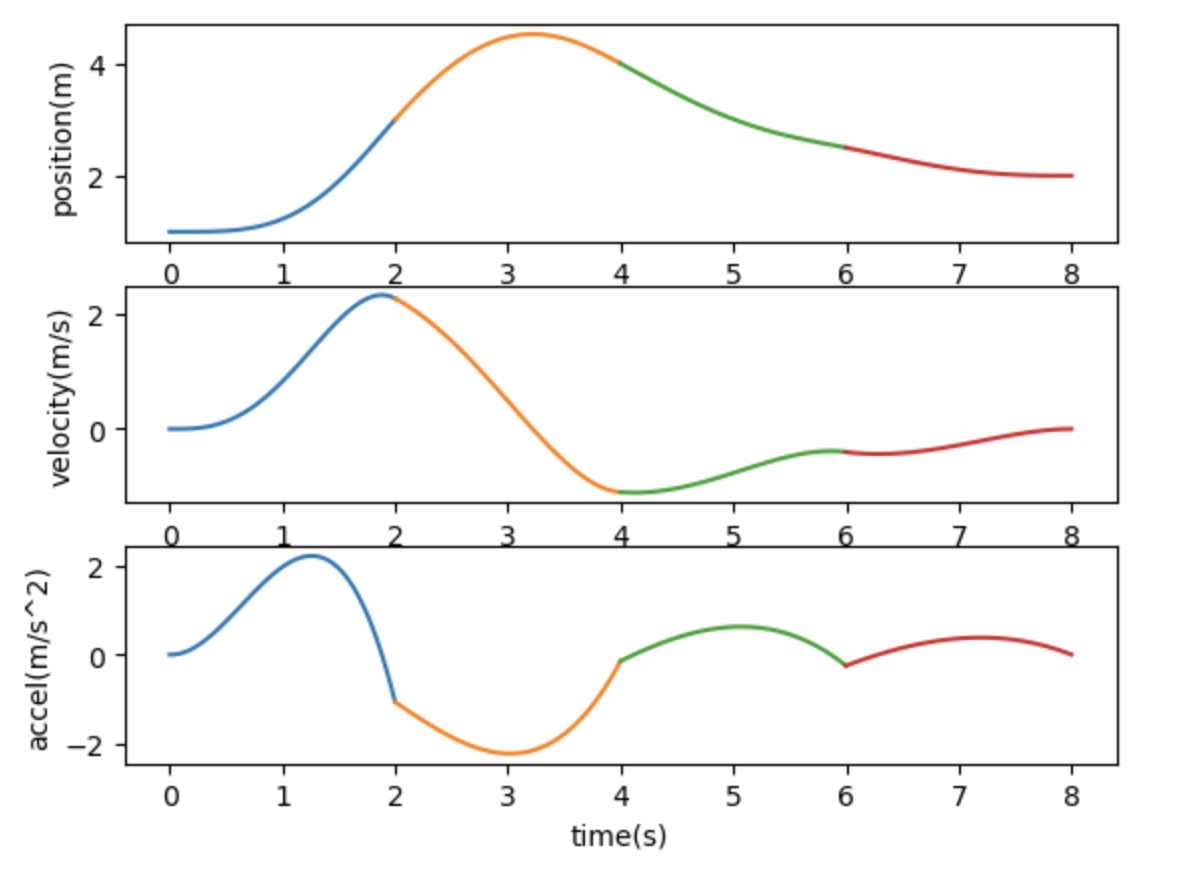

#%% 可视化结果
Pos = []
Vel = []
Acc = []
for k in range(M):t = np.linspace(T[k], T[k + 1], 100)t_pos = np.vstack((t**0, t**1, t**2, t**3, t**4, t**5))t_vel = np.vstack((t*0, t**0, 2 * t**1, 3 * t**2, 4 * t**3, 5 * t**4))t_acc = np.vstack((t*0, t*0, 2 * t**0, 3 * 2 * t**1, 4 * 3 * t**2, 5 * 4 * t**3))coef = p_coff[k * 6 : (k + 1) * 6]coef = np.reshape(coef, (1, 6))pos = coef.dot(t_pos)vel = coef.dot(t_vel)acc = coef.dot(t_acc)Pos.append([t, pos[0]])Vel.append([t, vel[0]])Acc.append([t, acc[0]])Pos = np.array(Pos)
Vel = np.array(Vel)
Acc = np.array(Acc)
plt.subplot(3, 1, 1)
plt.plot(Pos[:, 0, :].T, Pos[:, 1, :].T)
# plt.title("position")
plt.xlabel("time(s)")
plt.ylabel("position(m)")
plt.subplot(3, 1, 2)
plt.plot(Vel[:, 0, :].T, Vel[:, 1, :].T)
# plt.title("velocity")
plt.xlabel("time(s)")
plt.ylabel("velocity(m/s)")
plt.subplot(3, 1, 3)
plt.plot(Acc[:, 0, :].T, Acc[:, 1, :].T)
# plt.title("accel")
plt.xlabel("time(s)")
plt.ylabel("accel(m/s^2)")
plt.show()

二维求解&代码整合：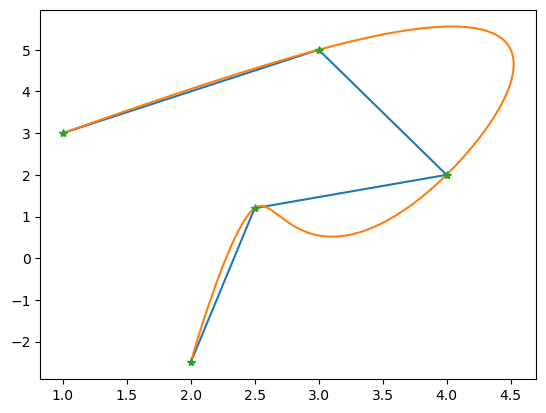

#%%
def trajectory_optimaze(x):# 分配时间deltaT = 2 # 每一段2秒T = np.linspace(0, deltaT * (len(x) - 1), len(x))########### 目标函数 ################### 1/2xTQx + qTx ########K = 3                   # jerk为3阶导数，取K=3n_order = 2 * K - 1     # 多项式阶数M = len(x) - 1          # 轨迹的段数N = M * (n_order + 1)   # 矩阵Q的维数def getQk(T_down, T_up):Q = np.zeros((6, 6))Q[3][4] = 36 * (T_up**2 - T_down**2)Q[3][5] = 40 * (T_up**3 - T_down**3)Q[4][5] = 60 * (T_up**4 - T_down**4)Q = Q + Q.T # Q为对称矩阵Q[3][3] = 36 * (T_up**1 - T_down**1)Q[4][4] = 48 * (T_up**3 - T_down**3)Q[5][5] = 80 * (T_up**5 - T_down**5)return QQ = np.zeros((N, N))for k in range(1, M + 1):Qk = getQk(T[k - 1], T[k])Q[(6 * (k - 1)) : (6 * k), (6 * (k - 1)) : (6 * k)] = QkQ = Q * 2 # 因为标准目标函数为： 1/2xTQx + qTx，所以要乘2########### 约束 ############ 1.导数约束 Derivative ConstraintA0 = np.zeros((2 * K + M - 1, N)) b0 = np.zeros(len(A0))# 添加首末状态约束(包括位置、速度、加速度)for k in range(K): for i in range(k, 6):c = 1for j in range(k):c *= (i - j)A0[0 + k * 2][i]                = c * T[0]**(i - k)A0[1 + k * 2][(M - 1) * 6 + i]  = c * T[M]**(i - k)b0[0] = x[0]b0[1] = x[M]# 添加每段轨迹的初始位置约束for m in range(1, M):for i in range(6):A0[6 + m - 1][m * 6 + i] = T[m]**ib0[6 + m - 1] = x[m]# 2.连续性约束 Continuity ConstraintA1 = np.zeros(((M - 1) * 3, N))b1 = np.zeros(len(A1))for m in range(M - 1):for k in range(3): # 最多两阶导数相等    for i in range(k, 6):c = 1for j in range(k):c *= (i - j)index = m * 3 + kA1[index][m * 6 + i] = c * T[m + 1]**(i - k)A1[index][(m + 1)* 6 + i] = -c * T[m + 1]**(i - k)A = np.vstack((A0, A1))b = np.hstack((b0, b1))#%% 解二次规划问题from cvxopt import matrix, solvers# 目标函数Q = matrix(Q)q = matrix(np.zeros(N))# 等式约束: Ax = bA = matrix(A)b = matrix(b)result = solvers.qp(Q, q, A=A, b=b)p_coff = np.asarray(result['x']).flatten()Pos = []Vel = []Acc = []for k in range(M):t = np.linspace(T[k], T[k + 1], 100)t_pos = np.vstack((t**0, t**1, t**2, t**3, t**4, t**5))t_vel = np.vstack((t*0, t**0, 2 * t**1, 3 * t**2, 4 * t**3, 5 * t**4))t_acc = np.vstack((t*0, t*0, 2 * t**0, 3 * 2 * t**1, 4 * 3 * t**2, 5 * 4 * t**3))coef = p_coff[k * 6 : (k + 1) * 6]coef = np.reshape(coef, (1, 6))pos = coef.dot(t_pos)vel = coef.dot(t_vel)acc = coef.dot(t_acc)Pos.append(pos)Vel.append(vel)Acc.append(acc)Pos = np.reshape(Pos, M * len(t))Vel = np.reshape(Vel, M * len(t))Acc = np.reshape(Acc, M * len(t))return [Pos, Vel, Acc]X = trajectory_optimaze(path[:, 0])
Y = trajectory_optimaze(path[:, 1])
plt.plot(path[:, 0], path[:, 1])
plt.plot(X[0], Y[0])
plt.plot(path[:, 0], path[:, 1], "*")
plt.show()

代微分约束的闭式求解：

$$\begin{gathered} min{\left[\begin{array}{c}{P}_0\\ P_1\\ ⋮\\ P_M\end{array}\right]}^T\left[\begin{array}{ccccc}{Q}_0& 0& \dots & \dots & 0\\ 0& Q_1& 0& \dots & 0\\ ⋮& ⋮& ⋮& \dots & ⋮\\ 0& 0& \dots & 0& Q_M\end{array}\right]\left[\begin{array}{c}{P}_0\\ P_1\\ ⋮\\ P_M\end{array}\right] \\ {\left[\begin{array}{c}{d}_0\\ d_1\\ ⋮\\ d_m\end{array}\right]}^T{\left[\begin{array}{ccccc}{A}_0& 0& \dots & \dots & 0\\ 0& A_1& \dots & \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & A_M\end{array}\right]}^{-T}\left[\begin{array}{ccccc}{Q}_0& 0& \dots & \dots & 0\\ 0& Q_1& 0& \dots & 0\\ ⋮& ⋮& ⋮& \dots & ⋮\\ 0& 0& \dots & 0& Q_M\end{array}\right]{\left[\begin{array}{ccccc}{A}_0& 0& \dots & \dots & 0\\ 0& A_1& \dots & \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & A_M\end{array}\right]}^{-1}\left[\begin{array}{c}{d}_0\\ d_1\\ ⋮\\ d_m\end{array}\right] \\ \Rightarrow min{d}^T{A}^{-T}{A}^{-1}d \end{gathered}$$
这部分只讲一句：所谓的闭式求解，所谓的代微分约束；其实就是说可以把约束条件整合到带价函数矩阵、向量中，而不是把约束条件放在约束条件中传入求解库代码中，差异就这么点。如何把约束条件塞进代价矩阵、向量理论部分看上面章节，具体实现可以结合理论推导结合下面的代码多看几遍，反复看反复测试验证自己的推理是不是对，最好可以把每个过程，每一步的矩阵参数打印出来验证。把参数量和矩阵大小、为何如此、输入是什么、如何转变要细细思考，不要怕麻烦，有难度但是并非难道不可理解，多花心思一定看得懂。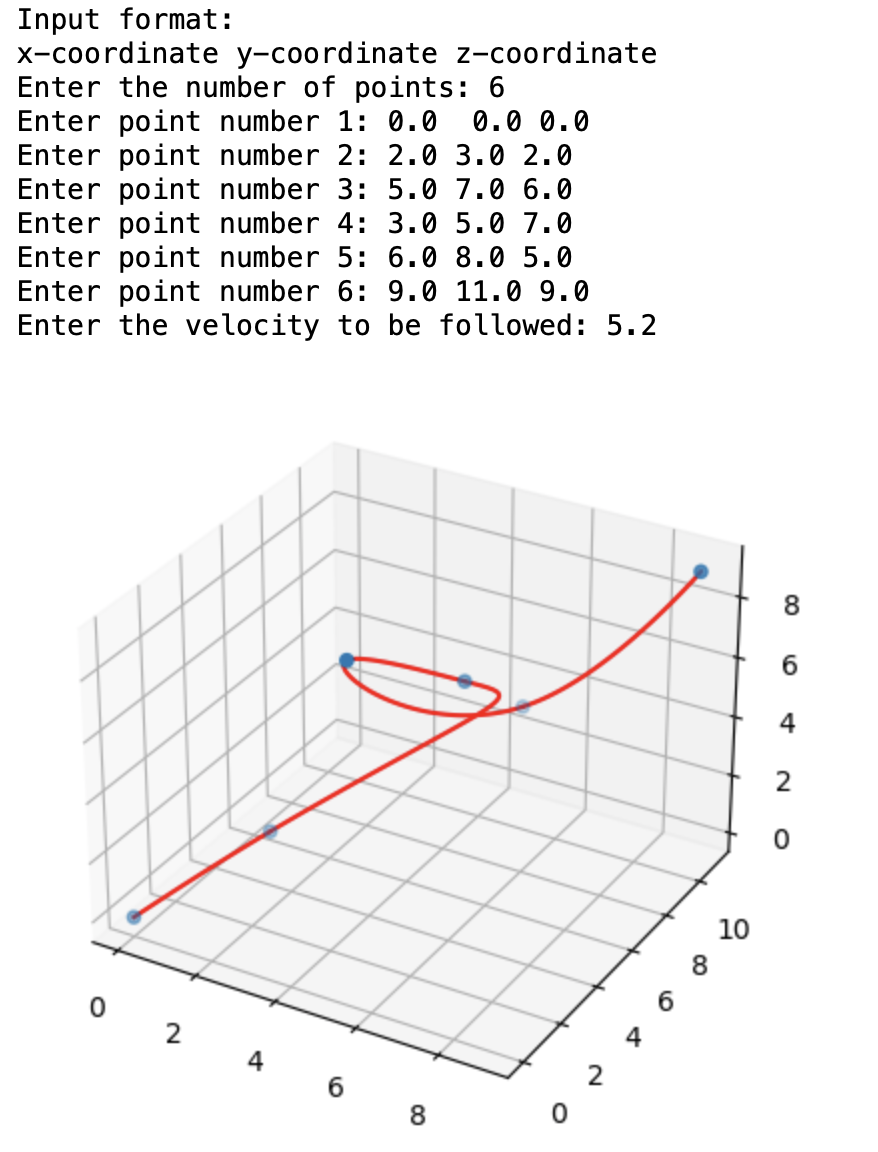

#pip install "qpsolvers[open_source_solvers]" -U  
from math import factorial 
from scipy.linalg import block_diag
import numpy as np
from qpsolvers import solve_qp
import matplotlib.pyplot as pltclass min_snap:def __init__(self,velocity, parameters):self.num_points = len(parameters) self.k = self.num_points - 1self.n = 7 self.get_points(parameters)self.velocity = velocityself.parameters = parametersself.time_stamps = self.get_time_stamps() self.Q = self.get_Q()self.A = self.get_A()self.b_x , self.b_y , self.b_z = self.get_b()self.q = np.zeros(((self.n+1) * self.k, 1)).reshape(((self.n+1)*self.k,))self.G = np.zeros((4 * self.k + 2, (self.n+1) * self.k))self.h = np.zeros((4 * self.k + 2, 1)).reshape((4 * self.k + 2, ))def get_points(self,parameters):x = []y = []z = []for point in parameters :x.append(point[0])y.append(point[1])z.append(point[2])self.x = xself.y = yself.z = zdef get_time_stamps(self):t = [0.1]parameters = self.parametersfor i in range(self.k):current_point = np.array(parameters[i])next_point = np.array(parameters[i+1])distance = np.linalg.norm(current_point - next_point)time_stamp = distance / self.velocityt.append(t[-1] + time_stamp) return tdef get_Q(self): Q_s = []n = self.n + 1t = self.time_stampsfor l in range (1,self.k+1):Q = np.zeros((n,n))for i in range(n):for j in range (n):if i > 3 and j > 3 :Q[i][j] = (factorial(i)*factorial(j)*(t[l]**(i + j - 7) - t[l-1]**(i + j - 7)))/(factorial(i-4) * factorial(j-4) * (i + j - 7))Q_s.append(Q)to_attach = Q_s[0]Q = []for i in range(len(Q_s) - 1):Q = block_diag(to_attach,Q_s[i+1])to_attach = QQ = Q + (0.0001 * np.identity((self.k*n))) # adding the term to ensure that Q is a positive definite matrixreturn Qdef get_A(self):k = self.kn = self.nA = np.zeros((4*k + 2 , k * (n + 1)))t = self.time_stampsfor j in range (n + 1):A[0][j] = t[0]**jA[1][j] = j*t[0]**(j-1)A[2][j] = j*(j-1)*t[0]**(j-2)for i in range (1, k) :for l in range (n+1):A[i + 2][(i-1) * (n + 1) + l] = t[i]**lfor j in range ((k - 1) * (n + 1), k * (n + 1)):r = j - (k - 1) * (n + 1)A[k+2][j] = t[k]**(r)A[k+3][j] = r*t[k]**(r-1)A[k+4][j] = r*(r-1)*t[k]**(r-2)for i in range(k-1):for l in range (2*n + 2):if l < (n + 1):A[k + 5 + 3 * i][(n+1)*i + l] = t[i + 1]**lA[k + 6 + 3 * i][(n+1)*i + l] = l*t[i + 1]**(l-1)A[k + 7 + 3 * i][(n+1)*i + l] = l*(l-1)*t[i + 1]**(l-2)else:A[k + 5 + 3 * i][(n+1)*i + l] = -t[i + 1]**(l-(n+1)) A[k + 6 + 3 * i][(n+1)*i + l] = -(l-(n+1))*t[i + 1]**((l-(n+1))-1)A[k + 7 + 3 * i][(n+1)*i + l] = -(l-(n+1))*((l-(n+1))-1)*t[i + 1] ** ((l-(n+1))-2)return Adef get_b(self):points = [self.x,self.y,self.z]b = []for i in range(3):bi = np.array([points[i][0], 0.0, 0.0])last_point = np.array([points[i][self.num_points-1], 0.0, 0.0])bi = np.append(bi, points[i][1:(self.num_points-1)])bi = np.append(bi, last_point)bi = np.append(bi,np.zeros((3*(self.k - 1))))b.append(bi)return bdef solve(self):self.p_x = solve_qp(self.Q,self.q,self.G,self.h,self.A,self.b_x, solver="osqp")self.p_y = solve_qp(self.Q,self.q,self.G,self.h,self.A,self.b_y, solver="osqp")self.p_z = solve_qp(self.Q,self.q,self.G,self.h,self.A,self.b_z, solver="osqp")def plot(self, time_resolution):plt.figure()ax = plt.axes(projection = '3d')ax.scatter(self.x, self.y, self.z, 'b', marker= 'o')self.solve()p_x, p_y, p_z = self.p_x, self.p_y, self.p_zfor i in range (self.k):x_segment = []y_segment = []z_segment = []t = np.linspace(self.time_stamps[i],self.time_stamps[i + 1], time_resolution)for j in range (time_resolution):x_term, y_term, z_term = 0, 0, 0for l in range ((self.n+1)*i, (self.n+1)*(i+1)):x_term = x_term + p_x[l]*(t[j]**(l-(self.n+1)*i))y_term = y_term + p_y[l]*(t[j]**(l-(self.n+1)*i))z_term = z_term + p_z[l]*(t[j]**(l-(self.n+1)*i))x_segment.append(x_term)y_segment.append(y_term)z_segment.append(z_term)ax.plot3D(x_segment,y_segment,z_segment, 'r')plt.show()if __name__ == '__main__':print ("Input format: ")print("x-coordinate y-coordinate z-coordinate")n = int(input("Enter the number of points: "))points = []for i in range(n):point = input(f"Enter point number {i+1}: ").split()x = float(point[0])y = float(point[1])z = float(point[2])points.append((x,y,z))v = float(input("Enter the velocity to be followed: "))minsnap = min_snap(v, points)minsnap.plot(100)

小结：

这篇文章详细的对轨迹生成框架minimum snap轨迹生成的推导和代码实现细节。这篇文章也是对上一篇文章的代码实现讲解。轨迹生成从本质来讲就是在做曲线拟合，只是在曲线拟合过程中要满足各种的约束。所以曲线拟合就会转成带约束的代价函数最小化规划问题，问题就转化为如何构建代价函数、如何构建约束条件；然后转成QP规划问题来求解答案就可以了。
在代码实现时候就会涉及到代价函数如何表达，如何把输入数据转成需要求解的形式；如何构建约束条件把输入构建成数据结构；以及会涉及如何把数据结构做效率优化，把带约束问题转成无约束问题提高求解难度和答案精度。这篇文章其实就是详细的介绍了理论和实际结合，讲解了Q｜A｜P｜d矩阵向量长成什么样、维度是如何、里面每部分数据如何、数据如何来、为何如此，代码如何实现。中间有什么问题，如何逐步的解决这些问题。总的文章框架是：多项式曲线拟合——>带约束代价函数QP规划——>闭式求解。总的来讲这是代码量和复杂度非常合适学习的做科研项目的方法，有框架逐步深入细节，如何逐步由简单到复杂。

参考：

https://blog.csdn.net/u011341856/article/details/121861930
https://dspace.mit.edu/bitstream/handle/1721.1/106840/Roy_Polynomial%20trajectory.pdf?sequence=1