数位统计DP

数位DP

数位（digit）指的是一个数字中的每一位。例如，对于整数1234来说，它有四个数位，分别是1、2、3和4。在数位统计 DP 中，我们通常将数字拆解成各个数位，并使用这些数位进行状态定义和转移。通过对每个数位进行状态定义和计算，我们可以解决各种数字相关的组合计数问题。

首先声明，我也是第一次涉及数位dp，是个菜鸡，因此只涉及最简单的数位问题。就我举的例子可能比较暴力，纯纯数学上的分类讨论，当然你也可以认为是dp中状态转移方程或者说集合划分的推导~

题目如下：

在这里插入图片描述
注意数据范围，别想着纯暴力~

用例输入输出：

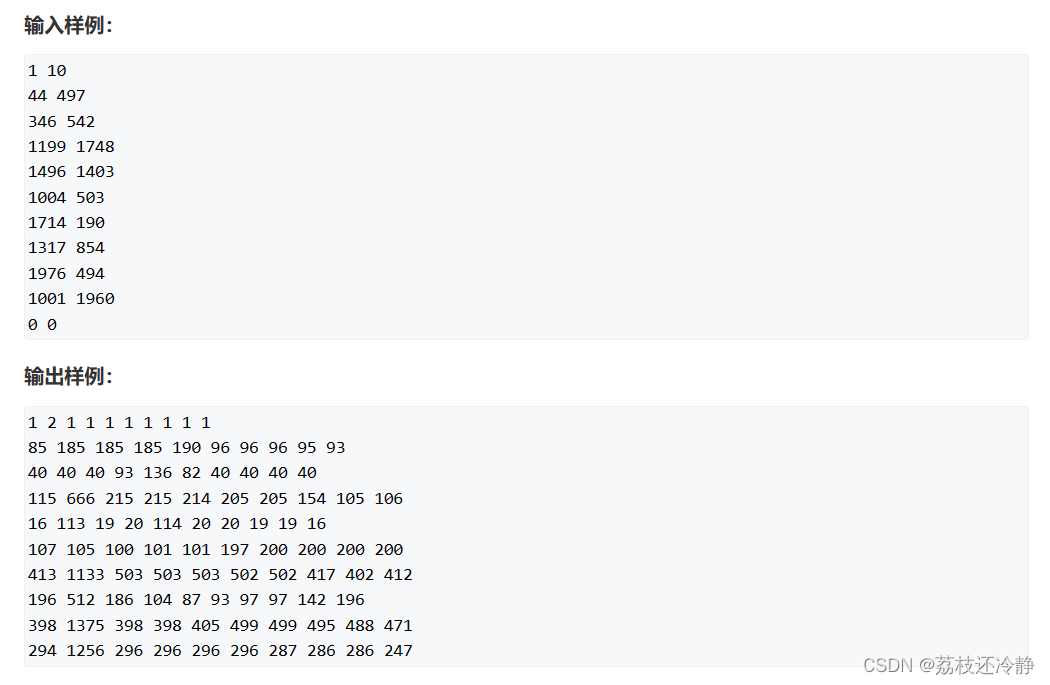
在这里插入图片描述
正常人思路: 暴力遍历一下范围内每一个数，再把每个数的每一位取出来，累计一下即可~时间复杂度少说O(n)，千万级别就够呛了，上亿那就死翘翘了必过不了。。
大佬们思路: 假设n=abcdefg，且第d位为1的情况——从0 ~ n这个范围内存在多少个xxx1yyy这样的数据呢？是不是可以粗略地说，有多少个就存在多少个1，至少就d这一位是可以这样统计出所有可能存在的1的一部分的。同理，我们依次假设在n的每一位上，当这一位为1的情况，是不是就可以统计出1~n中所有数据数位上1的情况？同理如果是2 ~ 9呢。是不是就可以统计出1 ~ 9在1 ~ n范围内分别出现多少次了。

在这里插入图片描述
上面count(b,x)-count(a-1,x)用到了前缀和的思想。

再跟着下面的图捋一下思路：

在这里插入图片描述

这里次数的计算和传统的状态转移方程不一样，而是通过简单的数学分析可以直接得出的。就以（1）为例：如果xxx=000~abc-1，是不是说明xxx一定小于abc，也就是说，不论后面efg数位上为什么，都不可能会大于abcdefg，也就是说efg三个数位上可选的组合为000 ~ 999一共1000个数，其实也就是10 ^3。三个位置嘛，每个位置有十种选法，也就是 10 ^3 注意这个指数写法，后面会用到。

假设n是1e8，亿级别的数据，也就9位罢了。十进制也就0 ~ 9十个数字。对于1 ~ n这个范围来说近乎是O(1)的了叭~ 这效率就离谱~

但是，最蚌埠住的就是编写代码了，相当考验思维的清晰程度，里面涉及好几个边界问题。比如：求0在第一位上出现的次数，即count(n,0)的情况，从这个数n的第1位上开始循环的时候就得因为这个特判一下，从第2位开始，即此时`abcdefg`就得从`b`这一位开始了。因为想构成数据至少为x0yyyy啥的，0yyyy直接击毙得了，因为总不能出现（-1）yyyy来凑次数叭，就是0；还有，求0在第2（3,4,5…）位上出现的次数呢。也会有边界问题，本来是000 ~ abc，如果d=0的话，前面就至少得从001 ~ abc叭。也就是说相当于（abc+1）10 ^3（假设为abcdefg）变成了（abc）10 ^3，少了一个10 ^3。

上面看不明白没关系，结合代码，你就会知道我举得例子多么珍贵了~

C++代码

#include <iostream>
#include <algorithm>
#include <vector>using namespace std;const int N = 10;/*001~abc-1, 999abc1. num[i] < x, 02. num[i] == x, 0~efg3. num[i] > x, 0~999*/int get(vector<int> num, int l, int r)
{int res = 0;for (int i = l; i >= r; i -- ) res = res * 10 + num[i];return res;
}int power10(int x)
{int res = 1;while (x -- ) res *= 10;return res;
}int count(int n, int x)
{if (!n) return 0;vector<int> num;while (n){num.push_back(n % 10);n /= 10;}n = num.size();int res = 0;for (int i = n - 1 - !x; i >= 0; i -- )//对x=0的特判，如果是0首位就跳过，这里本质是对n的每个位置进行处理。{if (i < n - 1){res += get(num, n - 1, i + 1) * power10(i);if (!x) res -= power10(i);//对x=0的特判}if (num[i] == x) res += get(num, i - 1, 0) + 1;else if (num[i] > x) res += power10(i);}return res;//这里得到的就是在1~n中所有数，的所有数位上，值为x的数目之和了
}int main()
{int a, b;while (cin >> a >> b , a){if (a > b) swap(a, b);for (int i = 0; i <= 9; i ++ )//这里十进制就处理0~9这十个数据就行cout << count(b, i) - count(a - 1, i) << ' ';cout << endl;}return 0;
}作者：yxc
链接：https://www.acwing.com/activity/content/code/content/64211/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。