Codeforces Round 913 (Div. 3)补题

 Rook

题目大意：我们给定一个棋盘(如下图)，棋盘上有一个车，问车可以到的位置，任意顺序输出即可。

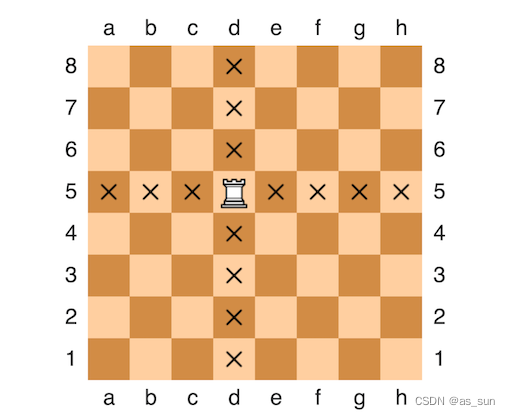
思路：输出车的行列中非它本身的点即可。

#include<bits/stdc++.h>
using namespace std;
int main()
{int t;scanf("%d",&t);while(t--){char s[3];scanf("%s",s);for(int i=1;i<=8;i++){if((s[1]-'0')!=i)printf("%c%d\n",s[0],i);}for(int i=0;i<8;i++){if('a'+i!=s[0]) printf("%c%c\n",'a'+i,s[1]);}}
}

 YetnotherrokenKeoard

 题目大意：我们需要输入一串字符，但是键盘上"b"按键出问题了，我们按下"b"时会删除最后一个小写字母，按下"B"时，会删除最后一个大写字母，如果待删除的字母不存在那么就不进行任何操作，我们需要输出最后的字串。

思路：这题的核心在于考虑最后哪些结果出现在答案中，因为涉及到大写和小写，而且还要分开删除，那么我们直接用两个容器来装访问到的字母，然后对应进行删除即可。最后输出只用按顺序输出即可，那么这个顺序是怎样的呢？我们记录下它们在原字串中的下标，然后按顺序输出即可（这里可以用下双指针）

#include<bits/stdc++.h>
using namespace std;
int main()
{int t;scanf("%d",&t);while(t--){string s;cin>>s;vector<pair<char,int>>d,x;for(int i=0;i<s.size();i++){if(s[i]=='B'){if(d.size()) d.pop_back();continue;}if(s[i]=='b'){if(x.size())x.pop_back();continue;}if('A'<=s[i]&&s[i]<='Z') d.push_back({s[i],i});if('a'<=s[i]&&s[i]<='z') x.push_back({s[i],i});}int i=0,j=0;while(i<d.size()&&j<x.size()){if(d[i].second<x[j].second) cout<<d[i].first,i++;else cout<<x[j].first,j++;}while(i<d.size()) cout<<d[i].first,i++;while(j<x.size())cout<<x[j].first,j++;cout<<endl;}
}

Removal of Unattractive Pairs

题目大意：有一串字符串，我们可以将相邻两个不同的字符删除，问我们删除尽可能多次后，剩下的字符串的长度最短是多少。

思路：我们可以发现，最后就算剩下也只能剩下一种字符，一旦有两种及以上字符剩下，那么必然存在两个相异的字符相邻，那么就必须删除。所以我们只用去统计每种字符出现的个数，并记录个数的最大值，如果最大值小于等于n/2那么 一定是可以全部消掉的，否则，最多的那个字母就会剩下，另外，要注意n为奇数，那么最终不管mx是多少，都会剩下一个字符，因为没有能跟它配对的了。

#include<bits/stdc++.h>
using namespace std;
char s[200010];
int main()
{int t;scanf("%d",&t);while(t--){int n;scanf("%d",&n);scanf("%s",s);map<char,int>mp;int mx=0;for(int i=0;i<n;i++) mp[s[i]]++,mx=max(mp[s[i]],mx);if(n%2){if(mx>n/2+1) mx -= (n-mx);else mx=1;}else{if(mx>n/2) mx -= (n-mx);else mx=0;}printf("%d\n",mx);}
}

Jumping Through Segments

题目大意：有n个区间，标号分别为1,2,..,n,它们都是x轴上的区间，我们初始在位置0，每次最多移动距离k,现在需要找到一个最小的k，使得第i次移动落在区间i内。

思路：这道题虽然一眼二分，但是check()很容易出差错，因为惯性思维还是考虑移动多少落在哪个点，然后就会去考虑每步怎么移动才是最优的。但是这是没必要的事情，这和另外一个题有点像（Absolute Sorting），不能考虑单点，需要考虑每次移动会落在哪个区间内。那么我们就从这个角度来考虑，首先每次的移动肯定要落在[l[i],r[i]]区间内部，在这个区间之外就没必要移动了，其次，我们假设上一次落在区间[L,R]内，那么能移动到的区间最多只能是[L-x,R+x](假设每次可以移动的最远距离是x)，那么我们实际上这一次移动合法且有效的区间就是两个区间取交集，那么这一次移动的落点区间就找出来了。判否的条件就是这两个区间没有交集，至此问题解决。

#include<bits/stdc++.h>
using namespace std;
int l[200010],r[200010];
int n;
bool check(int x)
{int L=0,R=0;for(int i=1;i<=n;i++){                            L=max(l[i],L-x);R=min(r[i],R+x);if(L>R) return false;}return true;
}
int main()
{int t;scanf("%d",&t);while(t--){scanf("%d",&n);int mx=0;for(int i=1;i<=n;i++) scanf("%d%d",&l[i],&r[i]),mx=max(mx,r[i]);int l=0,r=mx;while(l<r){int mid=(l+r)/2;if(check(mid)) r=mid;else l=mid+1;}printf("%d\n",l);}
}

ps:既然本题和Absolute Sorting比较像，那么我们就来顺便复习一下这道题。

题目大意：给定一个数组a[],我们需要对a[]进行排序，但是我们能进行的操作就是选定一个x,然后对于所有的ai,用|ai-x|替换ai，找出最小的x或者报告x不存在输出-1.

思路：这道题首先要明确|ai-x|表示的是距离（上次卡在这个地方，竟然没卡在从区间的角度考虑，还是得卡住才能影响深刻嘞，不过上次比较幸运最后想到了这个，直接把思路顺出来了），然后我们替换表示用距离去代替它们，所以很显然如果如果a[i]<a[i+1]那么选的x肯定要里a[i]更近，然后替换完两者的大小关系不会变，如果a[i]>a[i+1]那么两者的大小关系要改一下，那么就是选的x要离a[i+1]更近。这道题最开始也是想的考虑单点，即在最优策略下x选在哪个点，然后对其他的情况是否成立，但是很显然这个最优策略就很难评，所以后来想到去遍历确定x的合法区间，这个题甚至连二分都不用。因为这个题不需要知道具体x的值（而且这个题用二分还写不了，因为就算我们二分出x的值，判断对于所有的a[i]改变后是否成立，但是如果不成立，x该变大还是变小，我们并没有办法确定），上个题是不需要知道具体的区间落在哪里，但是转移需要x，所以需要二分x的值。但是它们的共同点都是去考虑合法区间而非单点。

Good Triples

题目大意：我们给定一个非负整数n，需要把n拆成3个数a,b,c，要求n=a+b+c,定义digit(n)为n的数位和，同时还要求:digit(n)=digit(a)+digit(b)+digit(c),求这样的三元组有多少个，同时规定[a,b,c]与[b,a,c]是两个三元组。

思路：我们首先来看，要使和和数位和都相等，那么a+b+c得是不进位直接加的，这样才能保证满足条件。那么就是对每一位上的数字进行拆解，那么拆解之后如何拼起来呢？我们可以发现，如果只将目光聚焦在每一位上的时候，那就相当于将当前这个数的这一组拆解放入3个容器，问有多少种放法，然后有多少组拆解，把它们的方法求和，就得到这一位能产生的不同情况，然后我们注意到，总共有若干位，将每一位的放法都求出来然后相乘即可。另外注意到，每一位上的数字都是0-9的，那么我们可以预处理一个数组出来，数值比较少，可以直接手算：

int a[]={1,3,6,10,15,21,28,36,45,55};

 那么问题就解决了。讲真这个题实际比D简单，如果D的那个点卡住的话，真不如先写E。

#include<bits/stdc++.h>
using namespace std;
int main()
{int a[]={1,3,6,10,15,21,28,36,45,55};int t;scanf("%d",&t);while(t--){int n;scanf("%d",&n);long long ans=1;if(n==0) ans=1ll;else{while(n){int d=n%10;ans *= (long long)a[d];n/=10;}}printf("%lld\n",ans);}
}

Shift and Reverse

题目大意：现有一个大小为n的数组a[],我们可以进行如下两个操作任意多次：

1.将末尾元素移到开头

2.将数组反转

我们最后需要使a[]变成非递减数组，问最少需要进行多少次操作，如果不管怎么操作都得不到就输出-1。

思路：我们来分析一下操作的实际意义。

我们将操作1命名为z,操作2命名为f。(一下描述中f或者z可能表示连着这么操作很多次)

对于数组:a[1]a[2]a[3]...a[n-2]a[n-1]a[n]:

z:a[n]a[1]a[2]a[3]...a[n-2]a[n-1]

f:a[n]a[n-1]a[n-2]...a[3]a[2]a[1]

fz:a[n]a[n-1]a[n-2]...a[3]a[2]a[1]->a[2]a[1]a[n]a[n-1]a[n-2]...a[3]

zf:a[n-1]a[n]a[1]a[2]a[3]...a[n-2]->a[n-2]...a[3]a[2]a[1]a[n]a[n-1]

fzf:a[n]a[n-1]a[n-2]...a[3]a[2]a[1]->a[2]a[1]a[n]a[n-1]a[n-2]...a[3]->

     a[3]...a[n-2]a[n-1]a[n]a[1]a[2]

zfz:a[n-1]a[n]a[1]a[2]a[3]...a[n-2]->a[n-2]...a[3]a[2]a[1]a[n]a[n-1]->

      a[n-1]a[n-2]...a[3]a[2]a[1]a[n](相当于zf中的z少执行几次而已，故而没有存在的必要)

fzfz:a[n]a[n-1]a[n-2]...a[3]a[2]a[1]->a[2]a[1]a[n]a[n-1]a[n-2]...a[3]->

     a[3]...a[n-2]a[n-1]a[n]a[1]a[2]->a[2]a[3]...a[n-2]a[n-1]a[n]a[1]

（相当于fzf中的z少执行几次而已，也没有存在的必要，后面就不用再讨论了，延伸不下去了。）

那么实际有效的只有z,f,fz,zf,fzf这几个操作，我们就对每个操作执行到底，看看能不能生成目标数组，如果可以取操作最小值，否则输出-1。另外记录一下，如果数组本身单增，那么输出0，单减输出1.

#include<bits/stdc++.h>
using namespace std;
int a[100010],b[100010],tmp[100010];
int n;
int z()
{//不管怎样都是转int c=a[1],idx=n+1;for(int i=n;i>=1;i--){if(a[i]<=c) c=a[i],idx=i;else break;}int j=0;for(int i=idx;i<=n;i++) tmp[++j]=a[i];for(int i=1;i<idx;i++) tmp[++j]=a[i];//判增c=tmp[1];idx=n-idx+1;for(int i=2;i<=n;i++){if(tmp[i]<c) {idx=-1;break;}c=tmp[i];}return idx;
}
int zf()
{//先转成单减的再反int c=a[1],idx=n+1;for(int i=n;i>=1;i--){if(a[i]>=c) c=a[i],idx=i;else break;}int j=0;for(int i=idx;i<=n;i++) tmp[++j]=a[i];for(int i=1;i<idx;i++) tmp[++j]=a[i];reverse(tmp+1,tmp+1+n);//判增c=tmp[1];idx=n-idx+1;idx += 1;for(int i=2;i<=n;i++){if(tmp[i]<c) {idx=-1;break;}c=tmp[i];}return idx;
}
int fz()
{int c=b[1],idx=n+1;for(int i=n;i>=1;i--){if(b[i]<=c) c=b[i],idx=i;else break;}int j=0;for(int i=idx;i<=n;i++) tmp[++j]=b[i];for(int i=1;i<idx;i++) tmp[++j]=b[i];//判增c=tmp[1];idx=n-idx+1;idx+=1;for(int i=2;i<=n;i++){if(tmp[i]<c) {idx=-1;break;}c=tmp[i];}return idx;
}
int fzf()
{reverse(a+1,a+1+n);int c=a[1],idx=n+1;for(int i=n;i>=1;i--){if(a[i]>=c) c=a[i],idx=i;else break;}int j=0;for(int i=idx;i<=n;i++) tmp[++j]=a[i];for(int i=1;i<idx;i++) tmp[++j]=a[i];reverse(tmp+1,tmp+1+n);//判增idx=n-idx+1;idx += 2;c=tmp[1];for(int i=2;i<=n;i++){if(tmp[i]<c) {idx=-1;break;}c=tmp[i];}return idx;
}
int main()
{int t;scanf("%d",&t);while(t--){scanf("%d",&n);int flag=0,gx=0;for(int i=1;i<=n;i++){scanf("%d",&a[i]);b[i]=a[i];if(i>1){if(gx==1&&a[i]<a[i-1]) flag=i;if(gx==2&&a[i]>a[i-1]) flag=i;if(!flag&&a[i]>a[i-1]) gx=1;if(!flag&&a[i]<a[i-1]) gx=2;}}reverse(b+1,b+1+n);/*转反反转转反反转反		*/if(flag)//非单调，仅仅反肯定不行了{//三种操作，取最小值或者输出-1int v1=z(),v2=zf(),v3=fzf(),v4=fz();if(v1!=-1||v2!=-1||v3!=-1) {if(v1==-1) v1=0x3f3f3f3f;if(v2==-1) v2=0x3f3f3f3f;if(v3==-1) v3=0x3f3f3f3f;if(v4==-1) v4=0x3f3f3f3f;int ans=min(v1,v2);ans=min(v3,ans);ans =min(v4,ans);printf("%d\n",ans);}else printf("-1\n");}else{if(gx<=1) printf("0\n");else printf("1\n");}}
}

反思：要通过这次的D记住有时候单点不能确定的时候，要考虑能不能确定点所在的区间，通过F要记住凡是讨论一定要把所有情况都讨论完整。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/202338.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Fabric:链码的部署及执行

Fabric:链码的部署及执行

Hyperledger Fabric:V2.5.4 写在最前 使用Fabric搭建自定义网络参考&#xff1a;https://blog.csdn.net/yeshang_lady/article/details/134113296 使用Fabric创建应用通道参考&#xff1a;https://blog.csdn.net/yeshang_lady/article/details/134668458 接下来将介绍如何在自…
阅读更多...
ELK的日志解决方案

ELK的日志解决方案

1. 安装和配置ELK 确保你已经安装了Elasticsearch、Logstash和Kibana。你可以按照官方文档或使用包管理工具进行安装。 Elasticsearch官方配置文档 Kibana官方配置文档 2. Logstash配置 拉取logstash 创建容器 docker run -it \ --name logstash \ --privileged \ -p 5044:5…
阅读更多...
Ubuntu-Sim2Real环境配置（下）

Ubuntu-Sim2Real环境配置（下）

cd ICRA-RM-Sim2Real/docker_client/ ./exec_client.sh cd ~ roslaunch rtab_navigation rtab_navigation.launch 执行上面代码的时候后台一直刷新 cd ICRA-RM-Sim2Real/docker_client/ ./exec_client.sh cd ~ roslaunch carto_navigation navigation.launch 1.Usage 执行该…
阅读更多...
【微服务】spring循环依赖深度解析

【微服务】spring循环依赖深度解析

目录 一、循环依赖概述 1.2 spring中的循环依赖 二、循环依赖问题模拟 2.1 循环依赖代码演示 2.2 问题分析与解决 2.2.1 使用反射中间容器 三、spring循环依赖问题解析 3.1 spring中的依赖注入 3.1.1 field属性注入 3.1.2 setter方法注入 3.1.3 构造器注入 3.2 spri…
阅读更多...
树莓派学习：wiringPi+硬件pwm+舵机

树莓派学习：wiringPi+硬件pwm+舵机

目录 目的 代码 只有io口1是支持pwm&#xff0c;其他要软件pwm 编译 运行 目的 黄色pwm&#xff0c;红色正极&#xff0c;棕色负极 让sg90舵机转动&#xff0c;就需要一个20ms的周期pwm&#xff0c;其中高电平在0.5-2.5ms之间 转动角度 高电平在一个周期内的时间0 …
阅读更多...
ElasticSearch篇---第四篇

ElasticSearch篇---第四篇

系列文章目录 文章目录 系列文章目录前言一、elasticsearch 是如何实现 master 选举的？二、elasticsearch 索引数据多了怎么办，如何调优，部署？三、说说你们公司 es 的集群架构，索引数据大小，分片有多少？前言 前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽…
阅读更多...
集成开发环境 PyCharm 的安装【侯小啾python基础领航计划 系列（二）】

集成开发环境 PyCharm 的安装【侯小啾python基础领航计划 系列（二）】

集成开发环境PyCharm的安装【侯小啾python基础领航计划 系列（二）】 大家好，我是博主侯小啾， 🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔…
阅读更多...
LeetCode Hot100 207.课程表

LeetCode Hot100 207.课程表

题目&#xff1a; 你这个学期必须选修 numCourses 门课程&#xff0c;记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出&#xff0c;其中 prerequisites[i] [ai, bi] &#xff0c;表示如果要学习课程 ai 则 必须 先学习…
阅读更多...
掌握大型语言模型（LLM）技术：推理优化

掌握大型语言模型（LLM）技术：推理优化

原文链接&#xff1a;Mastering LLM Techniques: Inference Optimization | NVIDIA Technical Blog 大模型相关技术文章已整理到Github仓库&#xff0c;欢迎start! 堆叠Transformer层以创建大型模型可以获得更好的准确性、few-shot学习能力&#xff0c;甚至在各种语言任务中具有…
阅读更多...
Kafka 的特点和优势

Kafka 的特点和优势

Apache Kafka 作为一款分布式流处理平台&#xff0c;以其独特的特点和卓越的优势成为实时数据处理领域的瑰宝。本文将深入研究 Kafka 的各项特点和优势&#xff0c;并通过详实的示例代码展示其在不同场景下的强大应用。 高吞吐量和水平扩展 Kafka 的设计注重高吞吐量和水平扩…
阅读更多...
Python-炸弹人【附完整源码】

Python-炸弹人【附完整源码】

炸弹人 炸弹人是童年的一款经典电子游戏&#xff0c;玩家控制一个类似"炸弹人"的角色&#xff0c;这个角色可以放置炸弹&#xff0c;并在指定的时间内引爆它们消灭敌人以达到目标&#xff0c;此游戏共设有两节关卡&#xff0c;代码如下&#xff1a; 运行效果&#x…
阅读更多...
python将时间戳转换为时间

python将时间戳转换为时间

python将时间戳转换为时间 import datetime timestamp 1701862813779 # 将时间戳转换为秒&#xff08;因为Python的timestamp通常是以秒为单位的&#xff09; timestamp_seconds timestamp / 1000 # 将时间戳转换为UTC时间 utc_time datetime.datetime.utcfromti…
阅读更多...
空间金字塔池化（SPP，Spatial Pyramid Pooling)系列

空间金字塔池化（SPP，Spatial Pyramid Pooling)系列

空间金字塔池化的作用是解决输入图片大小不一造成的缺陷&#xff0c;同时在目标识别中增加了精度。空间金字塔池化可以使得任意大小的特征图都能够转换成固定大小的特征向量&#xff0c;下面针对一些典型的空间金字塔进行盘点。 部分图片来自blog:空间金字塔池化改进 SPP / SP…
阅读更多...
每天一点python——day88

每天一点python——day88

#每天一点Python——88 #编程两大思想【面向过程与面向对象】 #如图&#xff1a; 面向过程的线性思维&#xff1a; 类似于做菜一步步的来&#xff0c;先怎么样怎么样&#xff0c;再怎么样 如果不一步步的来&#xff0c;例如先炒菜再点火&#xff0c;这样是做不好的 面向对象&a…
阅读更多...
IntelliJ IDE 插件开发 | （二）UI 界面与数据持久化

IntelliJ IDE 插件开发 | （二）UI 界面与数据持久化

系列文章 IntelliJ IDE 插件开发 |&#xff08;一&#xff09;快速入门 前言 在上一篇文章中介绍了在IDEA下开发、运行和安装插件的基本步骤&#xff0c;因此创建项目等基础步骤不再赘述&#xff0c;本文则开始介绍如何进行 UI 界面的开发以及相关数据的持久化存储&#xff…
阅读更多...
安全测试工具，自动发现网站所有URL！

安全测试工具，自动发现网站所有URL！

作为一个安全测试人员来说&#xff0c;首先要拿到网站所有url&#xff0c;然后根据拿到的url进行渗透测试进行漏洞挖掘。本文给大家介绍的是如何拿到一个网站所有的url。 深度爬取层级控制 现在我也找了很多测试的朋友&#xff0c;做了一个分享技术的交流群&#xff0c;共享了很…
阅读更多...
ospf选路

ospf选路

问题描述 R6通过主备份路径访问LSP&#xff08;R1&#xff09;&#xff0c;主为R2&#xff0c; 备为R3 解决方案 路由器1看作LSP&#xff0c;配置loopback 0 ,地址为1.1.1.1 供测试使用&#xff1b;路由器 236, LSW4和LSW5&#xff0c; 运行ospf处于相同区域&#xff0c;建立…
阅读更多...
Redis核心知识点总结

Redis核心知识点总结

1.Redis介绍 Redis 是 NoSQL&#xff0c;但是可处理 1 秒 10w 的并发&#xff08;数据都在内存中&#xff09; 使用 java 对 redis 进行操作类似 jdbc 接口标准对 mysql&#xff0c;有各类实现他的实现类&#xff0c;我们常用的是 druid 其中对 redis&#xff0c;我们通常用 J…
阅读更多...
16、XSS——会话管理

16、XSS——会话管理

文章目录 一、web会话管理概述1.1 会话管理1.2 为什么需要会话管理&#xff1f;1.3 常见的web应用会话管理的方式 二、会话管理方式2.1 基于server端的session的管理方式2.2 cookie-based的管理方式2.3 token-based的管理方式 三、安全问题 一、web会话管理概述 1.1 会话管理 …
阅读更多...
加速度jsudo:IC商城系统4.0版正式发布 PCB计价电子元器件商城

加速度jsudo:IC商城系统4.0版正式发布 PCB计价电子元器件商城

近日&#xff0c;在加速度软件新品会发布会上&#xff0c;Mike正式公布了其4.0版本的电子元器件商城系统&#xff0c;展示了迭代后的强大新功能。在招募了数十家元器件销售、运营和老板测试体验后&#xff0c;获得了大家一致的好评。其中&#xff0c;中国电子南京某子公司董事长…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023