使用t-SNE时，除了指定你想要降维的维度（参数n_components），另一个重要的参数是困惑度（Perplexity，参数perplexity）

困惑度：

困惑度大致表示如何在局部或者全局位面上平衡关注点，再说的具体一点就是关于对每个点周围邻居数量猜测。困惑度对最终成图有着复杂的影响。

1. 低困惑度对应的是局部视角，要把自己想象成一只蚂蚁，在数据所在的流形上一个点一个点地探索。
2. 高困惑度对应的是全局视角，要把自己想象成上帝。

参考：t-SNE：最好的降维方法之一 - 知乎 (zhihu.com)

具体介绍：

t-SNE（t-分布随机邻域嵌入，T-distributed Stochastic Neighbor Embedding）是一种流行的机器学习算法，主要用于降维。该算法特别适用于将高维数据映射到低维空间，如2维或3维，以便于可视化和分析。可以从具有数百甚至数千个维度的数据中创建引人注目的两维“地图”

t-SNE（t-DistributedStochastic Neighbor Embedding，T 分布随机近邻嵌入）是一种可以把高维数据降到二维或三维的降维技术。

t-SNE通过在低维空间中模拟高维数据分布，尽可能保留原始数据集中的局部结构。它是一种非线性降维技术，其核心思想是保持相似的数据点在嵌入后的空间中仍然彼此靠近，同时在高维空间中相隔较远的点在嵌入后也保持距离。

目标：

在高维空间中获取一组点，并在低维空间（通常是 2D 平面）中找到这些点的忠实表示。该算法是非线性的，可适应底层数据，在不同区域执行不同的变换。这些差异可能是造成混淆的主要根源。

t-SNE的第二个特点是一个可调的参数，即“困惑性”，它（松散地）表示如何平衡数据的局部和全局方面之间的注意力。从某种意义上说，该参数是对每个点具有的近邻数量的猜测。困惑度值对生成的图片具有复杂的影响。原始论文说，“SNE的性能对困惑度的变化相当鲁棒，典型值在5到50之间。但故事比这更微妙。从t-SNE中获得最大收益可能意味着分析具有不同困惑度的多个图。

算法的主要步骤包括：

1. 数据初始化：为数据集中的每个点分配一个随机的低维表示
2. 相似度计算：计算高维空间中所有点对之间的相似度，通常使用高斯分布来表示这种相似性。
3. 距离矩阵构建：根据相似度构建一个距离矩阵，这个矩阵描述了数据点在低维空间中的相对位置。
4. 概率分布学习：使用距离矩阵，通过极大似然估计学习一个用于生成低维表示的概率模型。
5. 优化：使用梯度下降法优化概率模型，迭代地更新低维表示，直到收敛。
6. 结果评估：使用一个称为“困惑度”的指标来评估最终嵌入的质量。

t-SNE在处理复杂数据集时表现出色，尤其是在数据可视化和发现数据的内在结构方面。但是，它也有一些局限性，比如计算复杂度高，对超参数（如困惑度）的选择敏感，以及在大数据集上可能需要大量的计算资源。

在R语言中，可以使用tsne包来进行t-SNE的计算和可视化。在Python中，sklearn.manifold库提供了t-SNE的实现，可以方便地对高维数据进行降维和可视化。

需要注意的是，t-SNE并不是唯一的选择。对于那些需要更快速处理且对内存要求较低的大数据集，可以选择UMAP（Uniform Manifold Approximation and Projection）作为替代方法，它也是一种非线性降维技术，特别适合于大规模数据集的降维和可视化。

与PCA方法的不同点：

参考：解读文献里的那些图——t-SNE散点图 - 知乎 (zhihu.com)

如果用 PCA 降维进行可视化，会出现所谓的“拥挤现象”。

相比于PCA，t-SNE更加注重保留原始数据的局部特征，这意味着高维数据空间中距离相近的点投影到低维中仍然相近，通过t-SNE处理同样能生成漂亮的可视化。

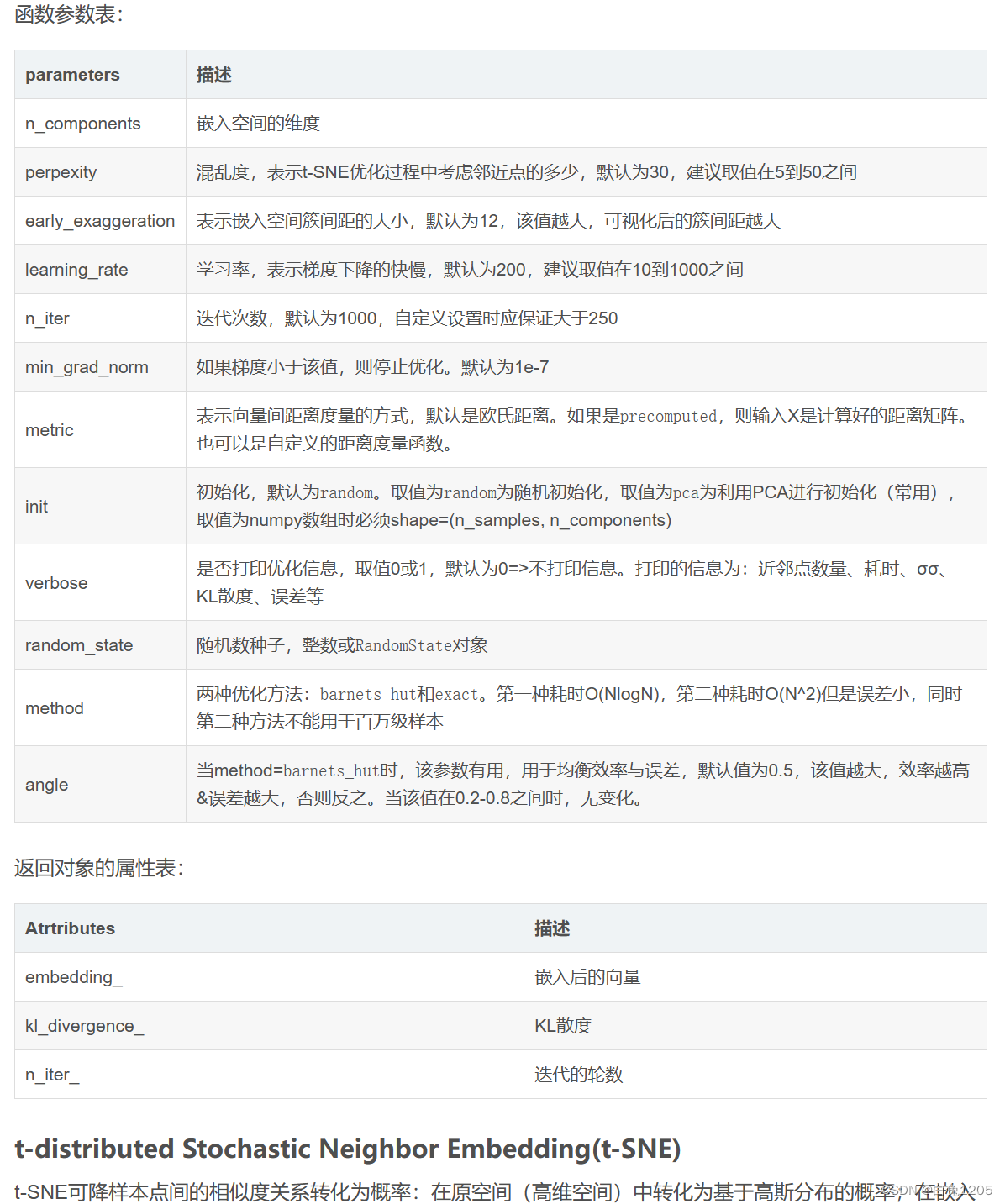
参数：

相关参考链接：

【1】如何有效使用t-SNE (distill.pub)

【2】t-SNE高维数据可视化（python）_t-sne可视化python-CSDN博客

【3】从SNE到t-SNE再到LargeVis (bindog.github.io)

【4】论文笔记：Visualizing data using t-SNE | 胡东瑶的小屋 (psubnwell.github.io)

【5】t-SNE：最好的降维方法之一 - 知乎 (zhihu.com)

【6】GitHub 上 - tensorflow/tfjs-tsne