引言
np.interp函数可对一维数组进行线性插值。具体来说,如果已知xp和yp,并且xp和yp具有确定的对应关系(比如yp=sin(xp)),那么对于新的一维数组x,可通过np.interp函数得到数组y,y是基于 xp和yp的映射关系 通过【线性插值】得到的。
代码
import numpy as np# 初始化一维数组xp
xp = np.linspace(0, 10, 20) # 从[0,10]这个范围等间隔取20个值
# 基于正弦函数对【离散】输入xp生成数组fp
fp = np.sin(xp) # fp = sin(xp)# 生成一批新的输入
x = np.linspace(0, 10, 100) # 从[0,10]这个范围等间隔取100个值
# 基于离散数组xp和fp的映射关系(正弦函数),对新的输入数组x预测对应的输出y(线性插值)
y = np.interp(x, xp, fp)# 绘制图像
import matplotlib.pyplot as plt
plt.axis("off")
plt.plot(xp, fp, 'o', markersize=10) # 原数组 xp fp均已知
plt.plot(x, y, 's', markersize=3) # 新数组 x已知,y是基于 xp与fp的映射关系 通过【线性插值】得到
plt.show()
运行结果
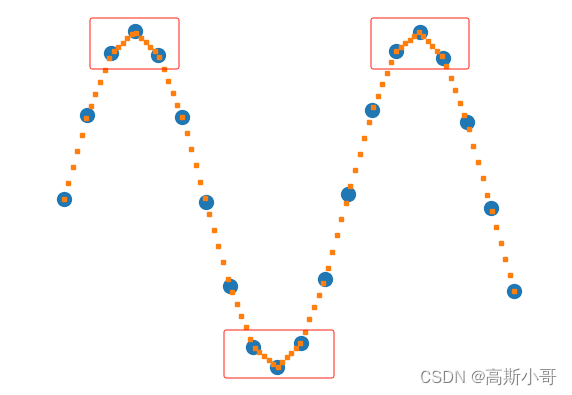
其中,原数组对(xp, yp)用蓝色圆点标记。很明显,(xp, yp)就是sin函数的离散采样点。而新数组(x, y)用橙色正方形标记。可以从上图红色框部分看出,y是基于xp与fp的映射关系 通过【线性插值】得到的。
结束语
如果本博文对你有所帮助,可以点个赞/收藏支持一下,如果能够持续关注,小编感激不尽~
如果有相关需求/问题需要小编帮助,欢迎私信~
小编会坚持创作,持续优化博文质量,给读者带来更好de阅读体验~








)





接口隔离原则)

)


)