题单来源：https://leetcode.cn/problems/minimum-size-subarray-in-infinite-array/solutions/2464878/hua-dong-chuang-kou-on-shi-jian-o1-kong-cqawc/

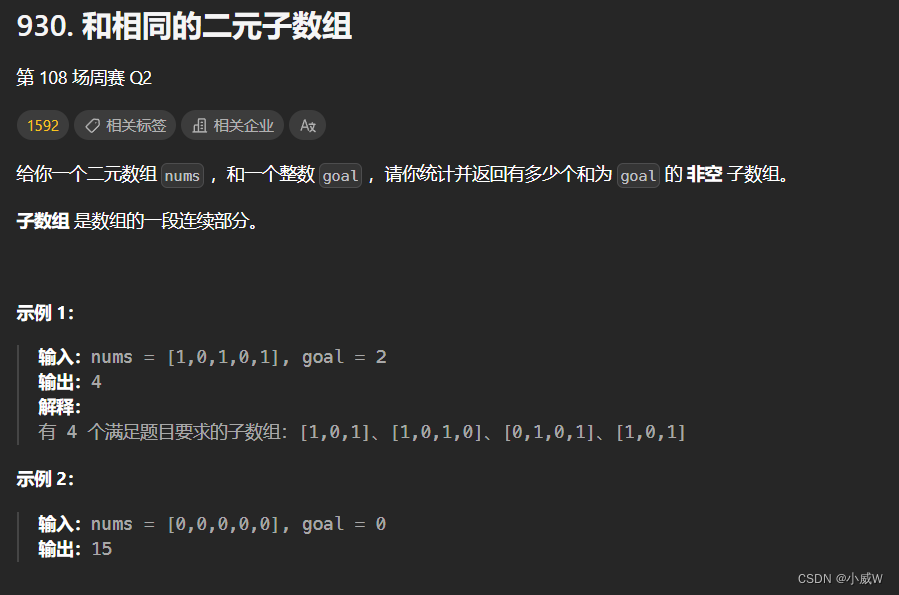
930. 和相同的二元子数组

https://leetcode.cn/problems/binary-subarrays-with-sum/description/

提示：

1 <= nums.length <= 3 * 10^4
nums[i] 不是 0 就是 1
0 <= goal <= nums.length

解法1——前缀和 + 哈希表

类似两数之和的思想。

class Solution {public int numSubarraysWithSum(int[] nums, int goal) {int n = nums.length;int[] s = new int[n + 1];for (int i = 0; i < n; ++i) {s[i + 1] = s[i] + nums[i];}int ans = 0;Map<Integer, Integer> cnt = new HashMap<>();cnt.put(0, 1);for (int i = 0; i < n; ++i) {int v = s[i + 1] - goal;ans += cnt.getOrDefault(v, 0);cnt.merge(s[i + 1], 1, Integer::sum);}return ans;}
}

解法2——滑动窗口 ⭐

class Solution {public int numSubarraysWithSum(int[] nums, int goal) {int n = nums.length, ans = 0, s1 = 0, s2 = 0;for (int l1 = 0, l2 = 0, r = 0; r < n; ++r) {s1 += nums[r];s2 += nums[r];// l1~r之和<=goalwhile (l1 <= r && s1 > goal) s1 -= nums[l1++];// l2~r之和<goalwhile (l2 <= r && s2 >= goal) s2 -= nums[l2++];ans += l2 - l1;     // 相减即为=goal的范围}return ans;}
}

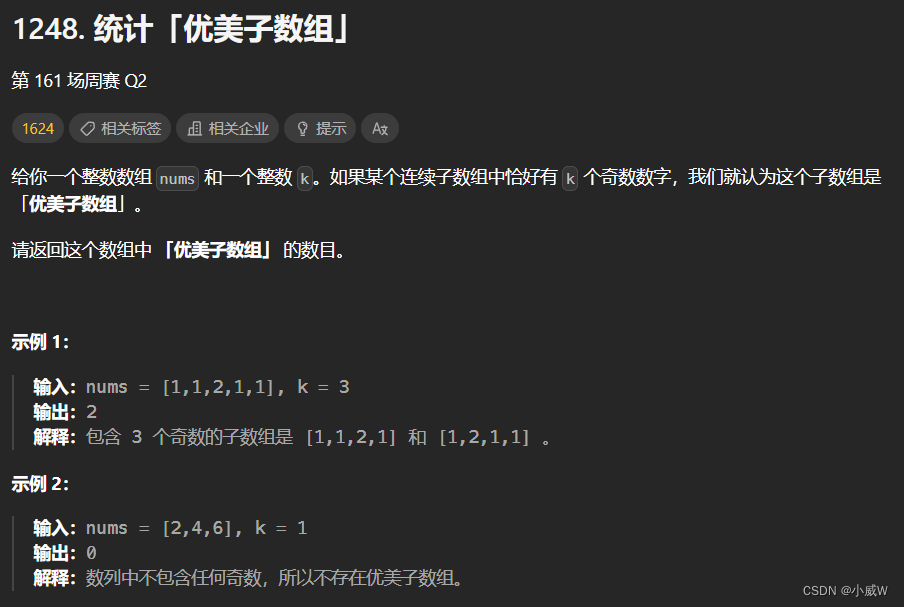
1248. 统计「优美子数组」

https://leetcode.cn/problems/count-number-of-nice-subarrays/description/

提示：

1 <= nums.length <= 50000
1 <= nums[i] <= 10^5
1 <= k <= nums.length

class Solution {public int numberOfSubarrays(int[] nums, int k) {int n = nums.length;int s1 = 0, s2 = 0, ans = 0;for (int l1 = 0, l2 = 0, r = 0; r < n; ++r) {if (nums[r] % 2 == 1) {s1++;s2++;}while (s1 > k) s1 -= nums[l1++] % 2;while (s2 >= k) s2 -= nums[l2++] % 2;ans += l2 - l1;}return ans;}
}

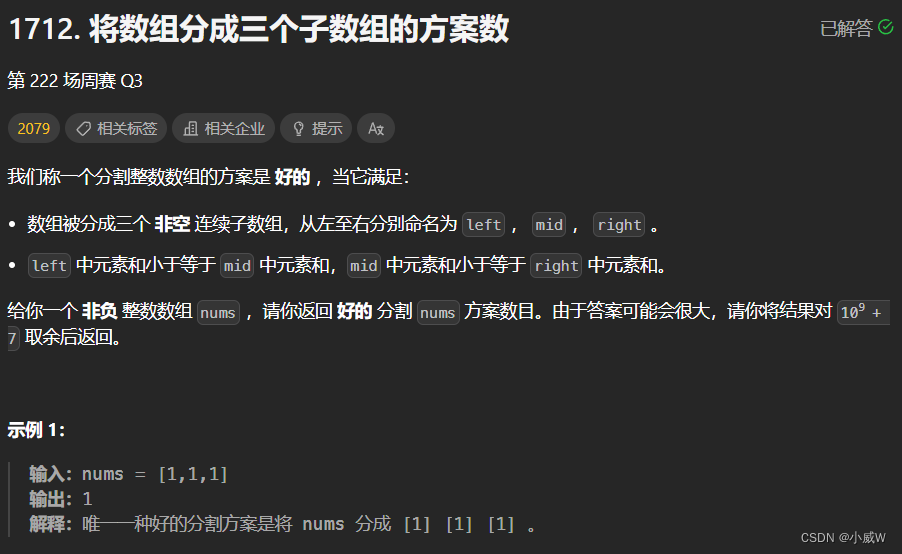
1712. 将数组分成三个子数组的方案数⭐⭐⭐

https://leetcode.cn/problems/ways-to-split-array-into-three-subarrays/description/

提示：
3 <= nums.length <= 10^5
0 <= nums[i] <= 10^4

枚举 i，0~i 作为第一个数组。
另外两个指针 j 和 k，对应第二个数组的结尾，分别是第二个数组右端点的可行范围两边。
当第二个数组不够大时，右移 j；当第二个数组还可以更大且不超过第三个数组时，右移 k。

class Solution {public int waysToSplit(int[] nums) {int n = nums.length;long[] s = new long[n + 1];for (int i = 0; i < n; ++i) {s[i + 1] = s[i] + nums[i];}final long MOD = (long)1e9 + 7;long ans = 0;// 0~i是第一个，i+1~j/k是第二个for (int i = 0, j = 1, k = 1; i < n - 2 && 3 * s[i + 1] <= s[n]; ++i) {j = Math.max(j, i + 1);while (j < n - 1 && s[j + 1] - s[i + 1] < s[i + 1]) j++;    // 不够大，右移while (k < n - 1 && s[n] - s[k + 1] >= s[k + 1] - s[i + 1]) k++;    // 还能更大，右移// 可取的范围是j~k-1ans = (ans + k - j) % MOD;}return (int)ans;}
}

2444. 统计定界子数组的数目

https://leetcode.cn/problems/count-subarrays-with-fixed-bounds/description/

提示：

2 <= nums.length <= 10^5
1 <= nums[i], minK, maxK <= 10^6

解法——多指针滑动窗口

使用两个 TreeMap 分别维护两个窗口中的最大值和最小值。
一个保证窗口中有 minK 和 maxK，另一个保证窗口中没有更大或更小的数字了。

class Solution {public long countSubarrays(int[] nums, int minK, int maxK) {int n = nums.length;TreeMap<Integer, Integer> tm1 = new TreeMap<>(), tm2 = new TreeMap<>();long ans = 0;for (int l1 = 0, l2 = 0, r = 0; r < n; ++r) {tm1.merge(nums[r], 1, Integer::sum);tm2.merge(nums[r], 1, Integer::sum);// l1确保没有更大或者更小的数字while (l1 <= r && (tm1.firstKey() < minK || tm1.lastKey() > maxK)) {tm1.merge(nums[l1], -1, Integer::sum);if (tm1.get(nums[l1]) == 0) tm1.remove(nums[l1]);l1++;}// l2确保有最小值和最大值while (l2 <= r && (tm2.firstKey() <= minK && tm2.lastKey() >= maxK)) {if (!((nums[l2] == minK || nums[l2] == maxK) && tm2.get(nums[l2]) == 0)) {tm2.merge(nums[l2], -1, Integer::sum);if (tm2.get(nums[l2]) == 0) tm2.remove(nums[l2]);l2++;}}ans += Math.max(0, l2 - l1);}return ans;}
}

代码2——简洁写法：一次遍历+O(1) 空间🐂⭐

https://leetcode.cn/problems/count-subarrays-with-fixed-bounds/solutions/1895713/jian-ji-xie-fa-pythonjavacgo-by-endlessc-gag2/

class Solution {public long countSubarrays(int[] nums, int minK, int maxK) {long ans = 0;int minI = -1, maxI = -1, i0 = -1;for (int i = 0; i < nums.length; ++i) {int x = nums[i];if (x == minK) minI = i;if (x == maxK) maxI = i;if (x < minK || x > maxK) i0 = i;ans += Math.max(0, Math.min(minI, maxI) - i0);}return ans;}
}

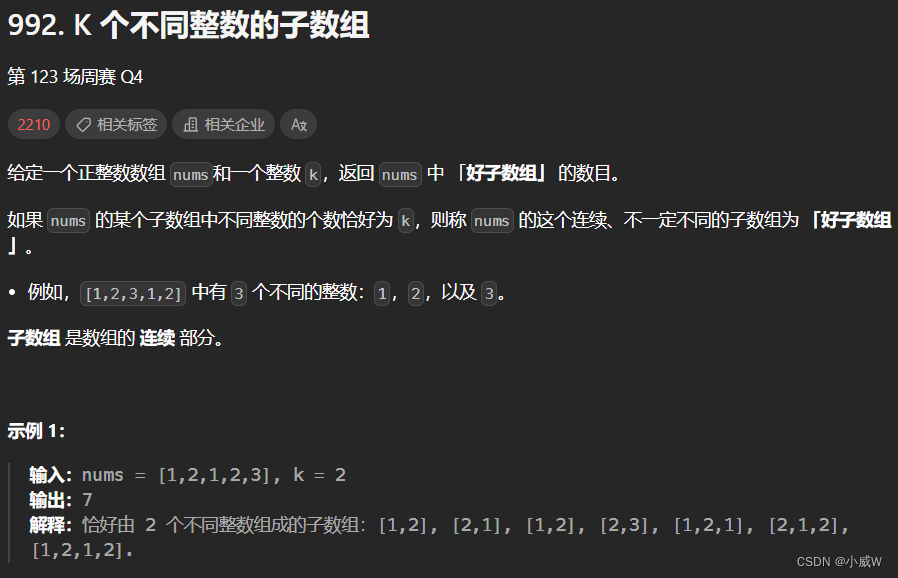
992. K 个不同整数的子数组

https://leetcode.cn/problems/subarrays-with-k-different-integers/description/

提示：
1 <= nums.length <= 2 * 10^4
1 <= nums[i], k <= nums.length

两个窗口分别保证窗口内不同元素的数量是 k 和 k - 1。
枚举右端点r，分别对应两个左端点l1和l2，l1~l2-1就是可选范围。

class Solution {public int subarraysWithKDistinct(int[] nums, int k) {int n = nums.length;int ans = 0;Map<Integer, Integer> m1 = new HashMap<>(), m2 = new HashMap<>();for (int l1 = 0, l2 = 0, r = 0; r < n; ++r) {m1.merge(nums[r], 1, Integer::sum);m2.merge(nums[r], 1, Integer::sum);while (m1.size() > k) {m1.merge(nums[l1], -1, Integer::sum);if (m1.get(nums[l1]) == 0) m1.remove(nums[l1]);l1++;}while (m2.size() > k - 1) {m2.merge(nums[l2], -1, Integer::sum);if (m2.get(nums[l2]) == 0) m2.remove(nums[l2]);l2++;}ans += l2 - l1;}return ans;}
}