1.Title
HGNN+: General Hypergraph Neural Networks(Yue Gao; Yifan Feng; Shuyi Ji; Rongrong Ji)【IEEE Transactions on Pattern Analysis and Machine Intelligence 2023】
2.Conclusion
This paper extend the original conference version HGNN, and introduce a general high-order multi-modal/multi-type data correlation modeling framework called HGNN + to learn an optimal representation in a single hypergraph based framework. In this method, hyperedge groups are first constructed to represent latent high-order correlations in each specific modality/type with explicit or implicit graph structures. An adaptive hyperedge group fusion strategy is then used to effectively fuse the correlations from different modalities/types in a unified hypergraph. After that a new hypergraph convolution scheme performed in spatial domain is used to learn a general data representation for various tasks.
3.Good Sentence
1、On one hand, the data correlation in the real world is far beyond pairwise correlation, which cannot be well modeled with a plain graph. For example, users in social networks may have different properties, and the correlation among those users could be in the manner of group, e.g., several users may share the same hobbies or are involved in the same event. Another limitation of simple graph is its weak capability in modeling multi-modal/multi-type real-world data.(The shortcoming of GNNs)
2、Here, we want to highlight the second fusion strategy: Adaptive Fusion. It associates each hyperedge group with a learnable parameter, thus adaptively identifying the importance of different hyperedge groups to the overall hypergraph representation learning and better exploiting the complementary representation of multi-modal/multi-type information(The innovative point of this paper)
3、However, considering that the information richness of different hyperedge groups varies a lot, such a simple Coequal Fusion cannot make full use of the multi-modal hybrid high-order correlations. Therefore, in this paper, we propose an adaptive strategy for the fusion of hyperedge groups, namely Adaptive Fusion.(The shortcomings of Coequal Fusion and how to improve it)
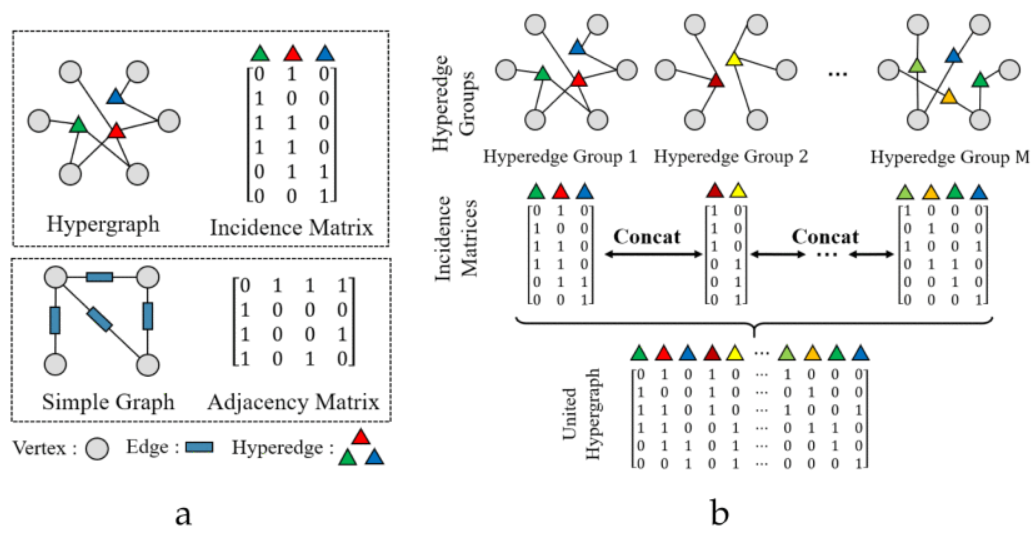 上如是超图与简单图的区别。
上如是超图与简单图的区别。
在本文中提出了基于超图卷积的表示学习来处理表示学习过程中的高阶数据相关性,并显示出不错的性能,该方法是 HGNN 的扩展,称为HGNN+。HGNN+的架构如图左部分所示,右边是一个超图卷积过程。
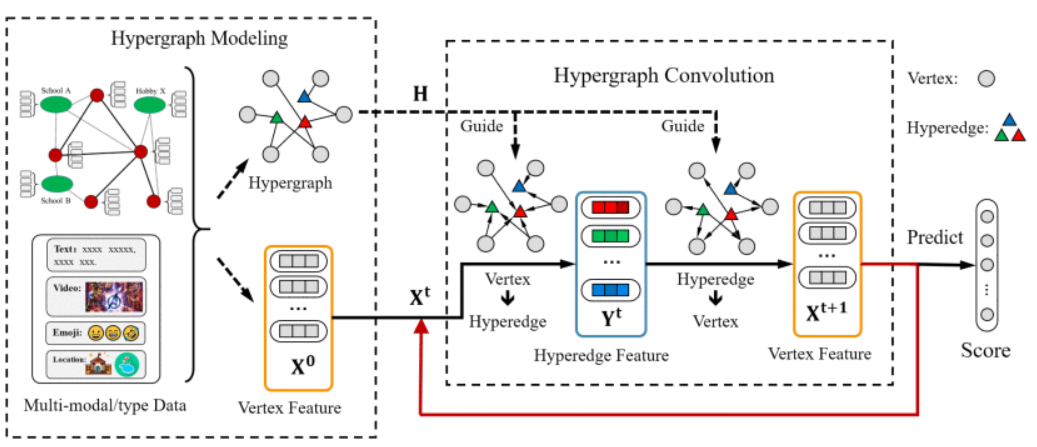
HGNN + 可以对高阶数据关联进行建模,并且易于与多模态/多类型数据融合。首先,为了更好地捕捉数据之间的底层高阶相关性,采用超图结构进行数据关联建模; 在处理多模态/多类型数据时,超图可以使用多模态/多类型数据生成不同类型的超边,然后直接将这些超边连接成一个超图。
hyperedge group:本文完善了超边组的概念。从数学上讲,超边组可以定义为节点集上的一个集合群组。而在节点集上,节点之间可能存在多类型关系。超边组可以基于一种关系构建,用以表示多重信息的不同特征。
本文将建模分为两个步骤:超边组构建和融合。在有/无图结构的数据下,引入4种类型的超边组来生成超图,即特征空间中的 成对边(using pairwise edge)、属性(attribute)、 k -Hop和邻居(neighbor)。
在生成多个超边组后,进一步有两种构建整体超图结构的方案。第一种是:直接连接不同的超边组的关联矩阵【Coequal Fusion】第二种是:将每个超边组与一个可学习参数相关联,从而自适应地识别不同超边组对整体超图表示学习的重要性,并更好地利用多模态/多类型信息的互补表示。【Adaptive Fusion】
超图任务:
给定一个超图,分类任务转向对超图上的顶点进行分类,其中超图上的标签需要通过超图结构进行平滑处理。该任务可以表述为正则化,如图: ![]() ,其中
,其中
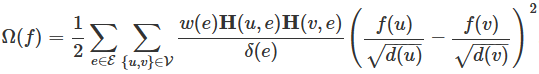 是正则化器,也是监督经验损失。
是正则化器,也是监督经验损失。![]() 是分类函数。
是分类函数。
令![]() ,那么上一个式子的矩阵形式为:
,那么上一个式子的矩阵形式为:![]() ,
,是超图拉普拉斯算子
超图神经网络HGNN + 的框架:
分两部分:超图生成和超图卷积。
超图建模:在大多数情况下数据没有明确的超图结构。因此,我们需要使用不同的策略生成超图。通常,从头开始生成超图的情况可以分为三种场景,即具有图结构的数据、没有图结构的数据和具有多模态/多类型表示的数据。目前有三种超边生成策略,分别是成对边、 k -Hop和邻居。成对边和 k -Hop可用于具有图结构的数据生成超边组,在特征空间中通过邻居法从无图结构的数据生成超边组。最后,所有超边组将被进一步连接以生成整体超图。
当数据关联与图结构相关时。在某些情况下,存在可用的成对数据关联,![]() 就是成对边,它的目标是直接将图结构转换为一组2-uniform的超边,如图所示
就是成对边,它的目标是直接将图结构转换为一组2-uniform的超边,如图所示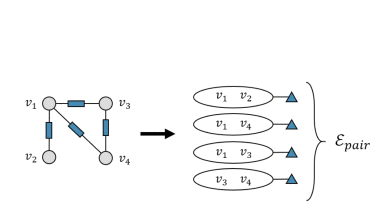
![]()
![]() 能够完全覆盖图结构中的低阶(成对)相关性,这是高阶相关性建模所需的基本信息
能够完全覆盖图结构中的低阶(成对)相关性,这是高阶相关性建模所需的基本信息
Hyperedge group using k-Hop neighbors :![]() 旨在通过图结构中的 k -Hop 可到达位置找到中心点的相关顶点
旨在通过图结构中的 k -Hop 可到达位置找到中心点的相关顶点![]() .带有k-Hop的超边组
.带有k-Hop的超边组![]() 可以写成:
可以写成:![]()
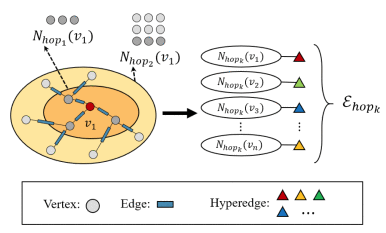
![]() 能够通过扩展图结构中的搜索半径来利用中心顶点的外部相关顶点,因此超边不止两个顶点组成,而是包含一组顶点
能够通过扩展图结构中的搜索半径来利用中心顶点的外部相关顶点,因此超边不止两个顶点组成,而是包含一组顶点
接下来是数据没有图结构时的方法
用属性的超边组。通过给定类似属性的数据,例如地理位置、时间和其他不同主体共享的特定信息,可以生成一组在属性空间中相邻的超边。其中每个超边代表一个属性(或属性的一个子类型)并连接共享同一属性 a 的所有主体。共享该属性 a 的顶点子集可以表示为![]()
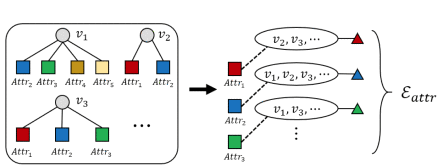
Hyperedge group using features
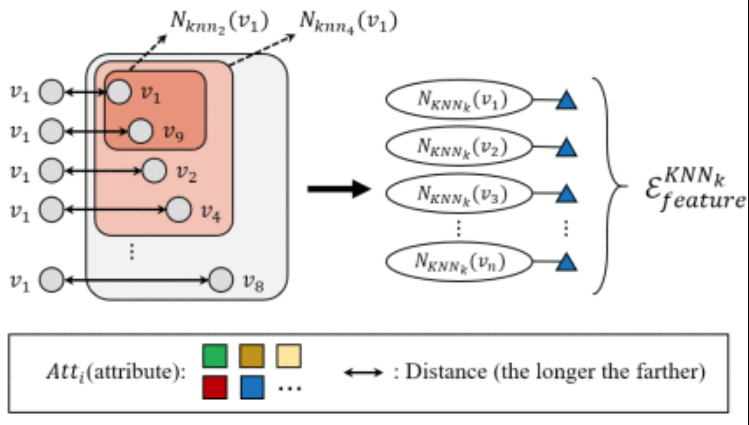
给定每个顶点的特征,可以通过在特征空间中查找每个顶点的邻居来生成![]() ,给定一个节点作为质心,可以通过K-近邻生成超边,也可以通过选择距离在d以内的所有节点生成超边
,给定一个节点作为质心,可以通过K-近邻生成超边,也可以通过选择距离在d以内的所有节点生成超边
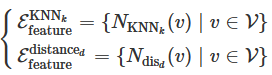
超边组连接成超图
通过上面的方法生成多个超边组以后,需要把它们组成起来形成最终所需要的超图。
构造超图G的关联矩阵的最简单的方法就是直接将所有超边连接为![]()
![]() ,所有超边的权重为1,这种方法就叫Coequal Fusion。
,所有超边的权重为1,这种方法就叫Coequal Fusion。
然而,考虑到不同超边的信息丰富度差异较大,这种简单的Coequal Fusion无法充分利用多模态混合高阶相关性。因此,本文提出了一种超边缘群融合的自适应策略,即自适应融合(Adaptive Fusion)。
自适应融合:
每个超边组都与一个可训练参数相关联,该参数可以自适应地调整多个超边组对最终顶点嵌入的影响。其定义为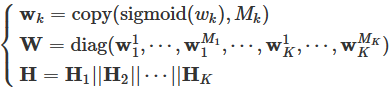
其中 ∈R 是指定超边组 k 内所有超边共享的可训练参数。
向量![]() 是超边组k的权重向量。
是超边组k的权重向量。
copy(a,b)是把a复制b次的函数,最后返回一个size为b的向量
![]() 表示所有超边组中超边的和
表示所有超边组中超边的和
W是一个代表权重的对角矩阵。
给定多模型/多类型数据,可以相应地生成多个超边组。从构建的超边组中生成超图关联矩阵 H 和超边权重矩阵 W ,然后将其输入到超图卷积层中进行进一步计算。
超图卷积
光谱卷积在AIII 2019的HGNN上提到了,这里仅关注空间上的卷积。
定义:对于超图中的每个顶点,聚合其相邻顶点信息,根据中心顶点与其邻域中每个顶点之间的“路径”进行自我更新。超图中的路径hyperpath,节点v1到vk的路径被定义为:![]() 超路径中的每两个相邻顶点都由一个超边分隔。两个顶点之间的超图中的信息通过相关的超边传输。
超路径中的每两个相邻顶点都由一个超边分隔。两个顶点之间的超图中的信息通过相关的超边传输。
对于消息的传播,首先,将超边集和节点集间的邻居关系定义为N。
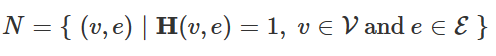
根据上式,可以定义超边的节点邻居和节点的超边邻居,分别如下


基于以上三个定义,假设给定一个顶点α,以及一个超图G,超图卷积的目标是从α的超边邻居集![]() 中聚合信息 ,而为了获得
中聚合信息 ,而为了获得![]() 中每个超边β的信息,又需要从超边β的顶点邻居集
中每个超边β的信息,又需要从超边β的顶点邻居集![]() 中聚合信息。这两个步骤形成了一个从节点特征信息集
中聚合信息。这两个步骤形成了一个从节点特征信息集到
的闭合传递循环。因此,第t层的空间域超图卷积可以定义为:

∈
是节点α∈V的在第t(=1,2,.....T)层时的输入特征向量,
是节点α的更新信息,
是超边β的信息,而
是与超边β相关联的权重,
是节点α的信息。
是超边β的超边特征
![]() 分别是第t层的节点信息函数、超边更新函数、超边信息函数和节点更新函数,可以针对指定的应用进行灵活定义
分别是第t层的节点信息函数、超边更新函数、超边信息函数和节点更新函数,可以针对指定的应用进行灵活定义
HGNNConv +:
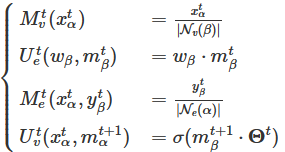
是第t层的可训练参数,σ(⋅) 是任意非线性激活函数,
![]() 和
和![]() 表示将节点特征和超边特征归一化,这能够累积收敛并在一定程度上防止抖动。
表示将节点特征和超边特征归一化,这能够累积收敛并在一定程度上防止抖动。
HGNNConv+的矩阵形式如下: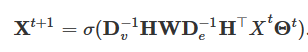








![[Java] 模拟Jdk 以及 CGLib 代理原理](http://pic.xiahunao.cn/[Java] 模拟Jdk 以及 CGLib 代理原理)





)


)

