实验6 二叉树操作

0x01 实验目的

掌握二叉树的基本概念，二叉树的存储结构使用链表。

0x02 实验内容

  1. 输入一个完全二叉树的层次遍历字符串，创建这个二叉树，输出这个二叉树的前序遍历字符串、中序遍历字符串、后序遍历字符串、结点数目、二叉树高度(上述每一个结果独立一行显示)。
  2. 输入二叉树前序序列和中序序列(各元素各不相同)，创建这个二叉树，输出该二叉树的后序序列、层次遍历。

0x03 实验过程

层次遍历

判断队列是否为空的条件必须加上，因为队列为空时，有可能会通过q.front()获取到一些非NULL的奇怪的东西，然后获取其element时会报错。

void levelOrder(binaryTreeNode<E>* node) {queue<binaryTreeNode<E>*> q;while (node != NULL) {if(Level == 0) {Level++;cout<<node->element;if(node->leftChild != NULL) q.push(node->leftChild);if(node->rightChild != NULL) q.push(node->rightChild);if(!q.empty()) {node = q.front();q.pop();}else node = NULL; } else {cout<<","<<node->element;if(node->leftChild != NULL) q.push(node->leftChild);if(node->rightChild != NULL) q.push(node->rightChild);if(!q.empty()) {node = q.front();q.pop();}else node = NULL; }}}

层次遍历构建二叉树

先将第一个节点放入队列，之后树上每添加一个节点就要将该节点入队列。先进先出的进行添加节点操作，直到node数组空了。

template <class E>
binaryTreeNode<E>* constructTreeByLevelOrder(binaryTreeNode<E> node[],int num) {queue<binaryTreeNode<E>*> q;q.push(&node[0]);int i = 1;while(i < num) {binaryTreeNode<E>* current = q.front();q.pop();if(i < num) {current->leftChild = &node[i];q.push(&node[i]);}i++;if(i < num) {current->rightChild = &node[i];q.push(&node[i]);}i++;}return &node[0];
}

前序遍历和中序遍历构建二叉树

采用递归地形式，依次构建左子树和右子树。利用前序遍历的的第一个节点是头节点，以及在中序遍历中头结点的两侧分别为左子树和右子树这两个性质。

template<class E>
binaryTreeNode<E>* create(binaryTreeNode<E> preorder[], int p, int q, binaryTreeNode<E> inorder[], int i, int j) {if (p > q) return nullptr;if (p == q) return &preorder[p];int k = i;// 找到根节点在中序遍历序列中的位置while (preorder[p].element != inorder[k].element) k++;preorder[p].leftChild = create(preorder, p+1, p+k, inorder, i, k-1);preorder[p].rightChild = create(preorder, p+k+1, q, inorder, k+1, j);return &preorder[p];
}

改BUG

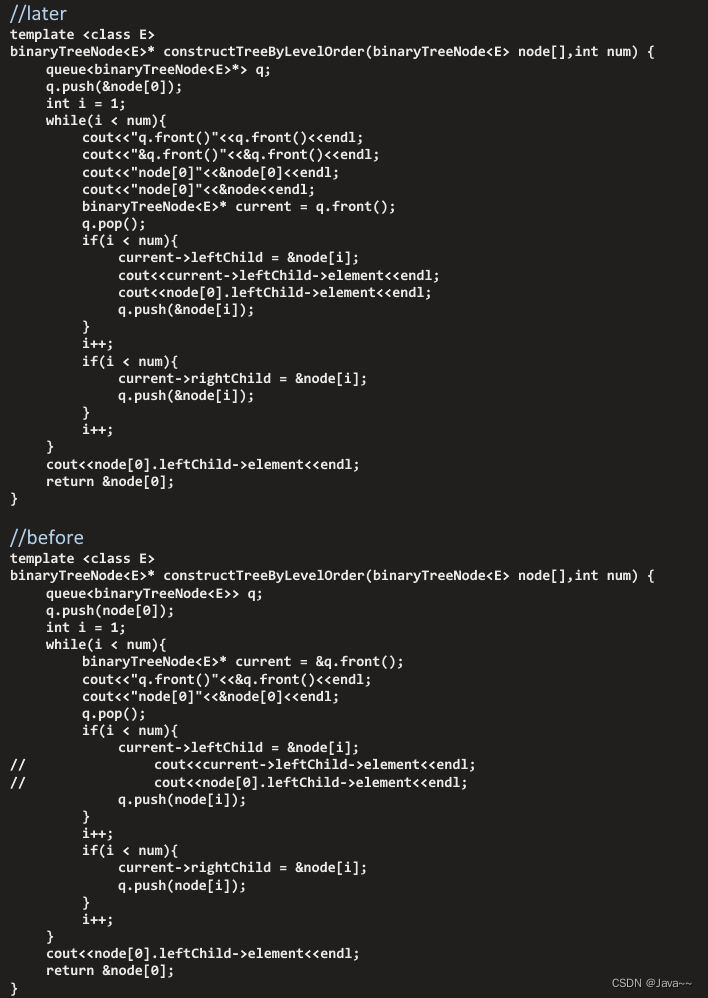
在这里插入图片描述
在这里插入图片描述

0x04 实验源码

#include<bits/stdc++.h>
using namespace std;
int in = 0;
int post = 0;
int Level = 0;
template<class T>
class binaryTreeNode {public:T element;binaryTreeNode<T> *leftChild,*rightChild;binaryTreeNode() {leftChild  = rightChild = NULL;}binaryTreeNode(const T& theElement) : element(theElement) {leftChild = rightChild = NULL;}binaryTreeNode(const T& theElement, binaryTreeNode *theLeftChild, binaryTreeNode *theRightChild):element(theElement) {leftChild = theLeftChild;rightChild = theRightChild;}
};
template<class E>
class linkedBinaryTree {public:linkedBinaryTree() {root = NULL;treeSize = 0;}bool empty() const {return treeSize == 0;}int size() const {return treeSize;}void setSize(int size) {treeSize = size;}void preOrder(binaryTreeNode<E>* node,int level) {if(node != NULL) {if(level == 0) {cout<<node->element;preOrder(node->leftChild, ++level);preOrder(node->rightChild, ++level);} else {cout<<","<<node->element;preOrder(node->leftChild, ++level);preOrder(node->rightChild, ++level);}}}void inOrder(binaryTreeNode<E>* node) {if(node != NULL) {if(node->leftChild == NULL && in == 0) {cout<<node->element;in++;} else {inOrder(node->leftChild);cout<<","<<node->element;inOrder(node->rightChild);}}}void postOrder(binaryTreeNode<E>* node) {if(node != NULL) {if(node->leftChild == NULL && post == 0) {cout<<node->element;post++;} else {postOrder(node->leftChild);postOrder(node->rightChild);cout<<","<<node->element;}}}void levelOrder(binaryTreeNode<E>* node) {queue<binaryTreeNode<E>*> q;while (node != NULL) {if(Level == 0) {Level++;cout<<node->element;if(node->leftChild != NULL) q.push(node->leftChild);if(node->rightChild != NULL) q.push(node->rightChild);if(!q.empty()) {node = q.front();q.pop();}else node = NULL; } else {cout<<","<<node->element;if(node->leftChild != NULL) q.push(node->leftChild);if(node->rightChild != NULL) q.push(node->rightChild);if(!q.empty()) {node = q.front();q.pop();}else node = NULL; }}}int getHeight(binaryTreeNode<E>* node) {if(node == NULL) return 0;int h1 = getHeight(node->leftChild);int h2 = getHeight(node->rightChild);if(h1 > h2) {return ++h1;} else {return ++h2;}}private:binaryTreeNode<E> *root;int treeSize;
};
template <class E>
binaryTreeNode<E>* constructTreeByLevelOrder(binaryTreeNode<E> node[],int num) {queue<binaryTreeNode<E>*> q;q.push(&node[0]);int i = 1;while(i < num) {
//		cout<<"q.front()"<<q.front()<<endl;
//		cout<<"&q.front()"<<&q.front()<<endl;
//		cout<<"node[0]"<<&node[0]<<endl;
//		cout<<"node[0]"<<&node<<endl;binaryTreeNode<E>* current = q.front();q.pop();if(i < num) {current->leftChild = &node[i];
//			cout<<current->leftChild->element<<endl;
//			cout<<node[0].leftChild->element<<endl;q.push(&node[i]);}i++;if(i < num) {current->rightChild = &node[i];q.push(&node[i]);}i++;}return &node[0];
}
template<class E>
binaryTreeNode<E>* create(binaryTreeNode<E> preorder[], int p, int q, binaryTreeNode<E> inorder[], int i, int j) {if (p > q) return nullptr;if (p == q) return &preorder[p];int k = i;// 找到根节点在中序遍历序列中的位置while (preorder[p].element != inorder[k].element) k++;preorder[p].leftChild = create(preorder, p+1, p+k, inorder, i, k-1);preorder[p].rightChild = create(preorder, p+k+1, q, inorder, k+1, j);return &preorder[p];
}
int main() {//两种写法都可以。//binaryTreeNode<char> *node = new binaryTreeNode<char>[100];binaryTreeNode<char> node[100];string s;cout<<"Input1"<<endl;cin>>s;for(int i = 0; i < s.length(); i++) {binaryTreeNode<char> n(s.at(i));node[i] = n;}linkedBinaryTree<char> tree;constructTreeByLevelOrder(node,s.length());tree.setSize(s.length());
//	node[0].leftChild = &node[1];
//	node[0].rightChild = &node[2];
//  cout<<"preOrder"<<endl;
//  记录层数，方便输出逗号int level = 0;cout<<"Output1"<<endl;
//	cout<<node[0].element<<endl;
//	cout<<node[0].leftChild<<endl;tree.preOrder(&node[0],level);cout<<endl;tree.inOrder(&node[0]);in = 0;cout<<endl;tree.postOrder(&node[0]);post = 0;cout<<endl;cout<<tree.size()<<endl;cout<<tree.getHeight(&node[0])<<endl;//	tree.constructTreeByLevelOrder(node,length);
//	tree.inOrder();
//	cout<<2<<node[0].element<<node[0].leftChild->element;cout<<"Input2"<<endl;string s1,s2;cin>>s1>>s2;binaryTreeNode<char> node1[100];binaryTreeNode<char> node2[100];for(int i = 0; i < s1.length(); i++) {binaryTreeNode<char> n(s1.at(i));node1[i] = n;}int noting;for(int i = 0; i < s2.length(); i++) {binaryTreeNode<char> n(s2.at(i));node2[i] = n;if(s2.at(i) == s1.at(0)) noting = i;}//constructTreeByPreOrderAndInOrder(node1, node2, s1.length(), s2.length(), noting);cout<<"Output2"<<endl;create(node1, 0, s1.length()-1, node2, 0, s2.length()-1);
//	tree.preOrder(&node1[0],level);
//	cout<<endl;
//	tree.inOrder(&node1[0]);
//	cout<<endl;tree.postOrder(&node1[0]);cout<<endl;tree.levelOrder(&node1[0]);cout<<endl;cout<<"End"<<endl;return 0;
}

0x05 错误代码

#include<bits/stdc++.h>
using namespace std;
int in = 0;
int post = 0;
int Level = 0;
template<class T>
class binaryTreeNode {public:T element;binaryTreeNode<T> *leftChild,*rightChild;binaryTreeNode() {leftChild  = rightChild = NULL;}binaryTreeNode(const T& theElement) : element(theElement) {leftChild = rightChild = NULL;}binaryTreeNode(const T& theElement, binaryTreeNode *theLeftChild, binaryTreeNode *theRightChild):element(theElement) {leftChild = theLeftChild;rightChild = theRightChild;}
};
template<class E>
class linkedBinaryTree {public:linkedBinaryTree() {root = NULL;treeSize = 0;}bool empty() const {return treeSize == 0;}int size() const {return treeSize;}void setSize(int size) {treeSize = size;}void preOrder(binaryTreeNode<E>* node,int level) {if(node != NULL) {if(level == 0) {cout<<node->element;preOrder(node->leftChild, ++level);preOrder(node->rightChild, ++level);} else {cout<<","<<node->element;preOrder(node->leftChild, ++level);preOrder(node->rightChild, ++level);}}}void inOrder(binaryTreeNode<E>* node) {if(node != NULL) {if(node->leftChild == NULL && in == 0) {cout<<node->element;in++;} else {inOrder(node->leftChild);cout<<","<<node->element;inOrder(node->rightChild);}}}void postOrder(binaryTreeNode<E>* node) {if(node != NULL) {if(node->leftChild == NULL && post == 0) {cout<<node->element;post++;} else {postOrder(node->leftChild);postOrder(node->rightChild);cout<<","<<node->element;}}}void levelOrder(binaryTreeNode<E>* node) {queue<binaryTreeNode<E>*> q;while (node != NULL) {if(Level == 0) {Level++;cout<<node->element;if(node->leftChild != NULL) q.push(node->leftChild);if(node->rightChild != NULL) q.push(node->rightChild);node = q.front();q.pop();} else {cout<<","<<node->element;if(node->leftChild != NULL) q.push(node->leftChild);if(node->rightChild != NULL) q.push(node->rightChild);node = q.front();q.pop();}}}int getHeight(binaryTreeNode<E>* node) {if(node == NULL) return 0;int h1 = getHeight(node->leftChild);int h2 = getHeight(node->rightChild);if(h1 > h2) {return ++h1;} else {return ++h2;}}private:binaryTreeNode<E> *root;int treeSize;
};
template <class E>
binaryTreeNode<E>* constructTreeByLevelOrder(binaryTreeNode<E> node[],int num) {queue<binaryTreeNode<E>*> q;q.push(&node[0]);int i = 1;while(i < num) {
//		cout<<"q.front()"<<q.front()<<endl;
//		cout<<"&q.front()"<<&q.front()<<endl;
//		cout<<"node[0]"<<&node[0]<<endl;
//		cout<<"node[0]"<<&node<<endl;binaryTreeNode<E>* current = q.front();q.pop();if(i < num) {current->leftChild = &node[i];
//			cout<<current->leftChild->element<<endl;
//			cout<<node[0].leftChild->element<<endl;q.push(&node[i]);}i++;if(i < num) {current->rightChild = &node[i];q.push(&node[i]);}i++;}return &node[0];
}
template <class E>
//左子树的实现 
binaryTreeNode<E>* soul(int noting, binaryTreeNode<E> node1[], binaryTreeNode<E> node2[]) {int index1 = 100;int index2 = 100;for(int i = 1; i <= noting; i++) {for(int j = noting; j >= 0; j--) {if(node1[i].element == node2[j].element) {index1 = index2;index2 = j;cout<<"index1"<<index1<<endl;cout<<"index2"<<index2<<endl;}}if(index1 > index2) {node1[i-1].leftChild = &node1[i];} else {
//			cout<<"Yes"<<endl;for(int j = noting; j >= 0; j--) {if(node1[i].element == node2[j].element) {for(int k = noting; k >= 0; k--) {if(node2[j-1].element == node1[k].element) {node1[k].rightChild = &node1[i];}}}}}}return &node1[0];
}
template <class E>
binaryTreeNode<E>* constructTreeByPreOrderAndInOrder(binaryTreeNode<E> node1[], binaryTreeNode<E> node2[], int num1, int num2, int noting) {soul(noting, node1, node2);int temp;//获取下一个左子树区间 for(int i = noting + 1; i < num1; i++) {if(node2[i].element == node1[noting+1].element) {temp = noting;noting = i;}}do {//重复操作，直到剩下最后一个元素，或者不剩下元素，退出循环 int num = 0;binaryTreeNode<char> node3[100];binaryTreeNode<char> node4[100];for(int i = temp + 1; i <= noting; i++) {node3[num] = node1[i];node4[num] = node2[i];num++;}soul(noting, node3, node4);for(int i = noting + 1; i < num1; i++) {if(node2[i].element == node1[noting+1].element) {temp = noting;noting = i;}}} while(noting + 1 != num1 - 1 && noting + 1 != num1);//如果剩一个元素 if(noting + 1 == num1 - 1) node2[num1 - 1].rightChild = &node2[num1];return &node1[0];
}
int main() {//binaryTreeNode<char> *node = new binaryTreeNode<char>[100];binaryTreeNode<char> node[100];string s;cout<<"Input"<<endl;cin>>s;for(int i = 0; i < s.length(); i++) {binaryTreeNode<char> n(s.at(i));node[i] = n;}linkedBinaryTree<char> tree;constructTreeByLevelOrder(node,s.length());tree.setSize(s.length());
//	node[0].leftChild = &node[1];
//	node[0].rightChild = &node[2];
//  cout<<"preOrder"<<endl;
//  记录层数，方便输出逗号int level = 0;cout<<"Output"<<endl;
//	cout<<node[0].element<<endl;
//	cout<<node[0].leftChild<<endl;tree.preOrder(&node[0],level);cout<<endl;tree.inOrder(&node[0]);in = 0;cout<<endl;tree.postOrder(&node[0]);post = 0;cout<<endl;cout<<tree.size()<<endl;cout<<tree.getHeight(&node[0])<<endl;//	tree.constructTreeByLevelOrder(node,length);
//	tree.inOrder();
//	cout<<2<<node[0].element<<node[0].leftChild->element;cout<<"Input2"<<endl;string s1,s2;cin>>s1>>s2;binaryTreeNode<char> node1[100];binaryTreeNode<char> node2[100];for(int i = 0; i < s1.length(); i++) {binaryTreeNode<char> n(s1.at(i));node1[i] = n;}int noting;for(int i = 0; i < s2.length(); i++) {binaryTreeNode<char> n(s2.at(i));node2[i] = n;if(s2.at(i) == s1.at(0)) noting = i;}constructTreeByPreOrderAndInOrder(node1, node2, s1.length(), s2.length(), noting);cout<<"Output2"<<endl;tree.preOrder(&node1[0],level);cout<<endl;tree.inOrder(&node1[0]);cout<<endl;tree.postOrder(&node1[0]);cout<<endl;tree.levelOrder(&node1[0]);cout<<endl;return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/194117.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

计算UDP报文CRC校验的总结

计算UDP报文CRC校验的总结

概述 因公司项目需求&#xff0c;遇到需要发送带UDP/IP头数据包的功能&#xff0c;经过多次尝试顺利完成&#xff0c;博文记录以备忘。 环境信息 操作系统 ARM64平台的中标麒麟Kylin V10 工具 tcpdump、wireshark、vscode 原理 请查看大佬的博文 UDP伪包头定义&#x…
阅读更多...
MQ - 消息系统

MQ - 消息系统

消息系统 1、消息系统的演变 在大型系统中&#xff0c;会需要和很多子系统做交互&#xff0c;也需要消息传递&#xff0c;在诸如此类系统中&#xff0c;你会找到源系统&#xff08;消息发送方&#xff09;和 目的系统&#xff08;消息接收方&#xff09;。为了在这样的消息系…
阅读更多...
数据结构和算法-哈夫曼树以相关代码实现

数据结构和算法-哈夫曼树以相关代码实现

文章目录 总览带权路径长度哈夫曼树的定义哈夫曼树的构造法1法2 哈夫曼编码英文字母频次总结实验内容&#xff1a; 哈夫曼树一、上机实验的问题和要求&#xff08;需求分析&#xff09;&#xff1a;二、程序设计的基本思想&#xff0c;原理和算法描述&#xff1a;三、调试和运行…
阅读更多...
Matter学习笔记（3）——交互模型

Matter学习笔记（3）——交互模型

一、简介 1.1 交互方式 交互模型层定义了客户端和服务器设备之间可以执行哪些交互。发起交互的节点称为发起者&#xff08;通常为客户端设备&#xff09;&#xff0c;作为交互的接收者的节点称为目标&#xff08;通常为服务器设备&#xff09;。 节点通过以下方式进行交互&a…
阅读更多...
Spring Initial 脚手架国内镜像地址

Spring Initial 脚手架国内镜像地址

官方的脚手架下载太慢了&#xff0c;并且现在没有了Java8的选项&#xff0c;所以找到国内的脚手架镜像地址&#xff0c;推荐给大家。 首先说官方的脚手架 官方的脚手架地址为&#xff1a; https://start.spring.io/ 但是可以看到&#xff0c;并没有了Java8的选项。 所以推荐…
阅读更多...
3dMax拼图生成工具Puzzle2D使用教程

3dMax拼图生成工具Puzzle2D使用教程

Puzzle2D for 3dsMax拼图生成工具使用教程 Puzzle2D简介&#xff1a; 2D拼图随机生成器&#xff08;英文&#xff1a;Puzzle2D&#xff09; &#xff0c;是一款由#沐风课堂#用MAXScript脚本语言开发的3dsMax建模小工具&#xff0c;可以随机创建2D可编辑样条线拼图图形。可批量…
阅读更多...
【tensorflow学习-选择动作】 学习tensorflow代码调用过程

【tensorflow学习-选择动作】 学习tensorflow代码调用过程

a actor.choose_action(s) def choose_action(self, s):s s[np.newaxis, :]return self.sess.run(self.action, {self.s: s}) # get probabilities for all actions输入&#xff1a;s 输出&#xff1a;self.sess.run(self.action, {self.s: s}) &#xff1a;a
阅读更多...
解决：UnboundLocalError: local variable ‘js’ referenced before assignment

解决：UnboundLocalError: local variable ‘js’ referenced before assignment

解决&#xff1a;UnboundLocalError: local variable ‘js’ referenced before assignment 文章目录 解决&#xff1a;UnboundLocalError: local variable js referenced before assignment背景报错问题报错翻译报错位置代码报错原因解决方法今天的分享就到此结束了 背景 在使…
阅读更多...
实战案例：chatglm3 基础模型多轮对话微调

实战案例：chatglm3 基础模型多轮对话微调

chatglm3 发布了&#xff0c;这次还发了base版本的模型&#xff0c;意味着我们可以基于这个base模型去自由地做SFT了。 本项目实现了基于base模型的SFT。 base模型 https://huggingface.co/THUDM/chatglm3-6b-base由于模型较大&#xff0c;建议离线下载后放在代码目录&#…
阅读更多...
OSG编程指南：专栏内容介绍及目录

OSG编程指南：专栏内容介绍及目录

1、专栏介绍 OpenSceneGraph&#xff08;OSG&#xff09;场景图形系统是一个基于工业标准 OpenGL 的软件接口&#xff0c;它让程序员能够更加快速、便捷地创建高性能、跨平台的交互式图形程序。本专栏基于 OSG 3.6.5版本进行源码的编写及扩展&#xff0c;也通用于其他OSG版本的…
阅读更多...
【书信，推荐信】【推荐节日活动】

【书信，推荐信】【推荐节日活动】

阅读更多...
OpenTelemetry系列 - 第2篇 Java端接入OpenTelemetry

OpenTelemetry系列 - 第2篇 Java端接入OpenTelemetry

目录 一、架构说明二、方式1 - 自动化2.1 opentelemetry-javaagent.jar&#xff08;Java8 &#xff09;2.2 使用opentelemetry-javaagent.jar完成自动注入2.3 配置opentelemetry-javaagent.jar2.4 使用注解&#xff08;WithSpan, SpanAttribute&#xff09;2.5.1 代码集成WithS…
阅读更多...
【栈和队列（2）】

【栈和队列（2）】

文章目录 前言队列队列方法队列模拟实现循环队列练习1 队列实现栈 前言 队列和栈是相反的&#xff0c;栈是先进后出&#xff0c;队列是先进先出&#xff0c;相当于排队打饭&#xff0c;排第一的是最先打到饭出去的。 队列 队列&#xff1a;只允许在一端进行插入数据操作&…
阅读更多...
20、Resnet 为什么这么重要

20、Resnet 为什么这么重要

&#xff08;本文已加入“计算机视觉入门与调优”专栏&#xff0c;点击专栏查看更多文章信息&#xff09; resnet 这一网络的重要性&#xff0c;上一节大概介绍了一下&#xff0c;可以从以下两个方面来有所体现&#xff1a;第一是 resnet 广泛的作为其他神经网络的 back bone&…
阅读更多...
Redis集合对象

Redis集合对象

一. 编码 集合对象的编码可以是intset或者hashtable。 intset编码的集合对象使用整数集合作为底层实现&#xff0c;集合对象包含的所有元素都保存在整数集合里面。 127.0.0.1:6379> sadd numbers 1 3 5 (integer) 3 127.0.0.1:6379> object encoding numbers "ints…
阅读更多...
使用凌鲨进行内网穿透

使用凌鲨进行内网穿透

为了方便在本地进行开发和调试工作&#xff0c;有时候需要安全地连接内网或Kubernetes集群中的服务。 在net proxy server中可以限制访问用户&#xff0c;也可以设置端口转发的密码。 使用 连接端口转发服务 列出可转发端口 可转发端口是服务端设置的&#xff0c;不会暴露真…
阅读更多...
锁表的原因及解决办法

锁表的原因及解决办法

引言 作为开发人员&#xff0c;我们经常会和数据库打交道。 当我们对数据库进行修改操作的时候&#xff0c;例如添加字段&#xff0c;更新记录等&#xff0c;没有正确评估该表在这一时刻的使用频率&#xff0c;直接进行修改&#xff0c;致使修改操作长时间无法响应&#xff0…
阅读更多...
2023年【起重机司机(限桥式起重机)】报名考试及起重机司机(限桥式起重机)考试资料

2023年【起重机司机(限桥式起重机)】报名考试及起重机司机(限桥式起重机)考试资料

题库来源&#xff1a;安全生产模拟考试一点通公众号小程序 2023年【起重机司机(限桥式起重机)】报名考试及起重机司机(限桥式起重机)考试资料&#xff0c;包含起重机司机(限桥式起重机)报名考试答案和解析及起重机司机(限桥式起重机)考试资料练习。安全生产模拟考试一点通结合…
阅读更多...
正是阶段高等数学复习--函数极限的计算

正是阶段高等数学复习--函数极限的计算

之前在预备阶段中函数极限的解决方式分三步&#xff0c;第一步观察形式并确定用什么方式来解决&#xff0c;第二步化简&#xff0c;化简方式一共有7种&#xff0c;分别是最重要的三种&#xff08;等价替换、拆分极限存在的项、计算非零因子&#xff09;以及次重要的4种&#xf…
阅读更多...
BurpSuite 请求/响应解密插件开发

BurpSuite 请求/响应解密插件开发

BurpSuite 请求/响应解密插件开发 本文主要记录如何利用burp官方的新版API即MontoyaApi 写一个请求/响应的解密插件。背景下面是主要的操作步骤&#xff1a;根据上述操作做完之后&#xff0c;生成&#xff0c;然后在burp中加载插件&#xff0c;然后通关抓包看效果&#xff0c;具…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023