目录

题目描述

题解

思路分析

暴力枚举代码

滑动窗口代码

---

题目描述

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2

输入：target = 4, nums = [1,4,4]
输出：1

题解

思路分析

题目要求我们找到和 >= target 的 最小 且 连续 的子数组，我们很容易想到暴力枚举的方法，即访问数组的每一个元素i，并将i作为第一个元素，向后寻找

暴力枚举代码

class Solution {public int minSubArrayLen(int target, int[] nums) {int count = 0;for(int i = 0; i < nums.length; i++){int sum = 0;//向后遍历找到以nums[i]为起始元素的最小数组for(int j = i; j < nums.length;j++){sum += nums[j];if(sum >= target){//更新目标值 由于count的初始值为0，因此需要更新初始值，//否则最小值恒为0if(count > j-i+1 || count == 0){count = j-i+1;}break;}}}//若count未被更新，则返回0，即没有子数组的和大于target，//若count被跟新，则返回最小的子数组长度return count;}
}

 

此时我们通过遍历访问了数组的每个元素，在访问每个元素时，以该元素为起始元素，并向后寻找其最小长度的子数组，因此时间复制度为O()

而，题目所给的数组中所有元素均是正整数，因此每加上一个元素，子数组的和 sum 增加，通过这个特性，我们可以想到使用滑动窗口来解决这个问题

什么是滑动窗口？

滑动窗口是一种基于双指针的思想，两个指针指向的元素之间形成了一个窗口

因此滑动窗口是通过两个指针来维护的，那么如何移动这两个指针，是使用滑动窗口解决问题的关键

 初始时，两个指针都指向0下标位置

遍历元素，若条件不满足，则将right指针向右移动，直到条件满足为止

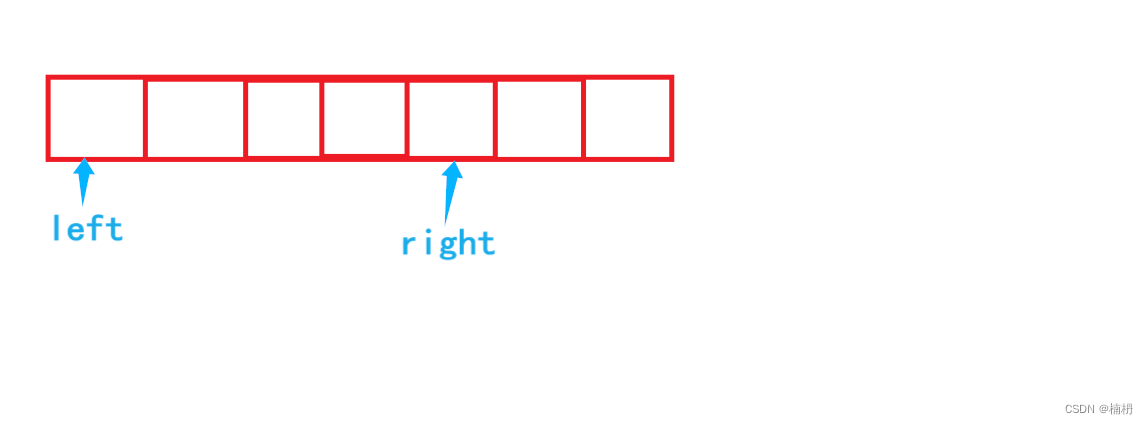
当条件满足时，则保持右指针不变，开始移动左指针 left

在向窗口中添加新元素或从窗口中删除旧元素时，可能会更新一些与窗口范围有关的数据（例如，本题就需要更新最小子数组的长度）

如何使用滑动窗口解决本题？ 

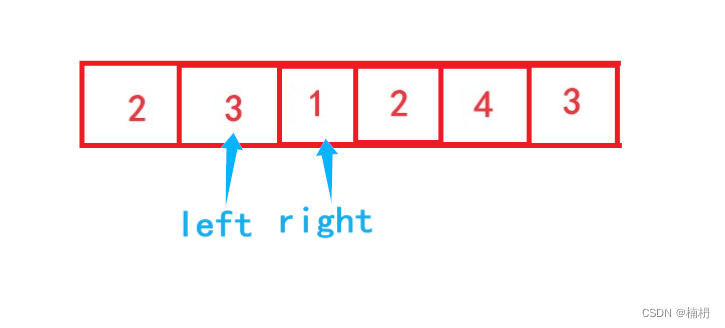
（1）我们定义两个指针left right，并让其都指向数组首元素

 

（2）此时窗口内只有 2 这一个元素，不满足和 sum >= target，因此将right向右移动，将新的元素加入窗口中，并判断此时子数组的和 sum 是否大于等于target，若满足，则不再移动right

（3）在sum >= target时，首先判断最小的子数组长度是否需要更新，并保持right不变，向右移动左指针left，删除旧的元素，直到sum < target

（4）循环（2）（3），直到right遍历完数组

为什么可以使用滑动窗口解决本题？
 

因为我们要找的子数组是连续的，且数组中的元素都为正整数，即子数组中增加一个元素，子数组中的元素和sum增加，从窗口中删除一个元素，sum减小，因此我们可以通过改变子数组的两端元素来更新数组，因此可以使用滑动窗口来解决本题

由于左右指针都只遍历了一遍数组，因此时间复杂度为O(N)

滑动窗口代码

class Solution {public int minSubArrayLen(int target, int[] nums) {int left = 0;int right = 0;int sum = nums[0];int len = nums.length;int count = 0;while(left <= right && right < len){//小于目标值，向右移动右指针rightwhile(left <= right && right < len && sum < target){right++;if(right == len){break;}sum += nums[right];}//大于等于目标值while(left <= right && sum >= target){//更新目标值 由于count的初始值为0，因此需要更新初始值，否则最小值恒为0if((right - left) < count || count == 0){count = right - left + 1;}//左边值出窗口，left向右移动sum -= nums[left];left++;}}//若count未被更新，则返回0，即没有子数组的和大于target，//若count被跟新，则返回最小的子数组长度return count;}
}

题目来自：

LCR 008. 长度最小的子数组 - 力扣（LeetCode）