作者：小猪快跑

基础数学&计算数学，从事优化领域5年+，主要研究方向：MIP求解器、整数规划、随机规划、智能优化算法

如有错误，欢迎指正。如有更好的算法，也欢迎交流！！！——@小猪快跑

相关文献

• Making a flat list out of list of lists in Python
• Most efficient way to map function over numpy array
• numpy: most efficient frequency counts for unique values in an array
• Most efficient way to reverse a numpy array
• How to add an extra column to an numpy array
• Initializing numpy matrix to something other than zero or one

测试电脑配置

博主三千元电脑的渣渣配置：

CPU model: AMD Ryzen 7 7840HS w/ Radeon 780M Graphics, instruction set [SSE2|AVX|AVX2|AVX512]
Thread count: 8 physical cores, 16 logical processors, using up to 16 threads

展开元素是list的list

输入：

[[1, 2, 3],[4, 5, 6],[7],[8, 9]
]

输出：

[1, 2, 3, 4, 5, 6, 7, 8, 9]

我们从两个维度测试，一种是sub-list的元素数量固定，增加list里面的元素：

f = lambda n: [list(range(10))] * n
f(1) = [[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]
f(3) = [[0, 1, 2, 3, 4, 5, 6, 7, 8, 9], [0, 1, 2, 3, 4, 5, 6, 7, 8, 9], [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]

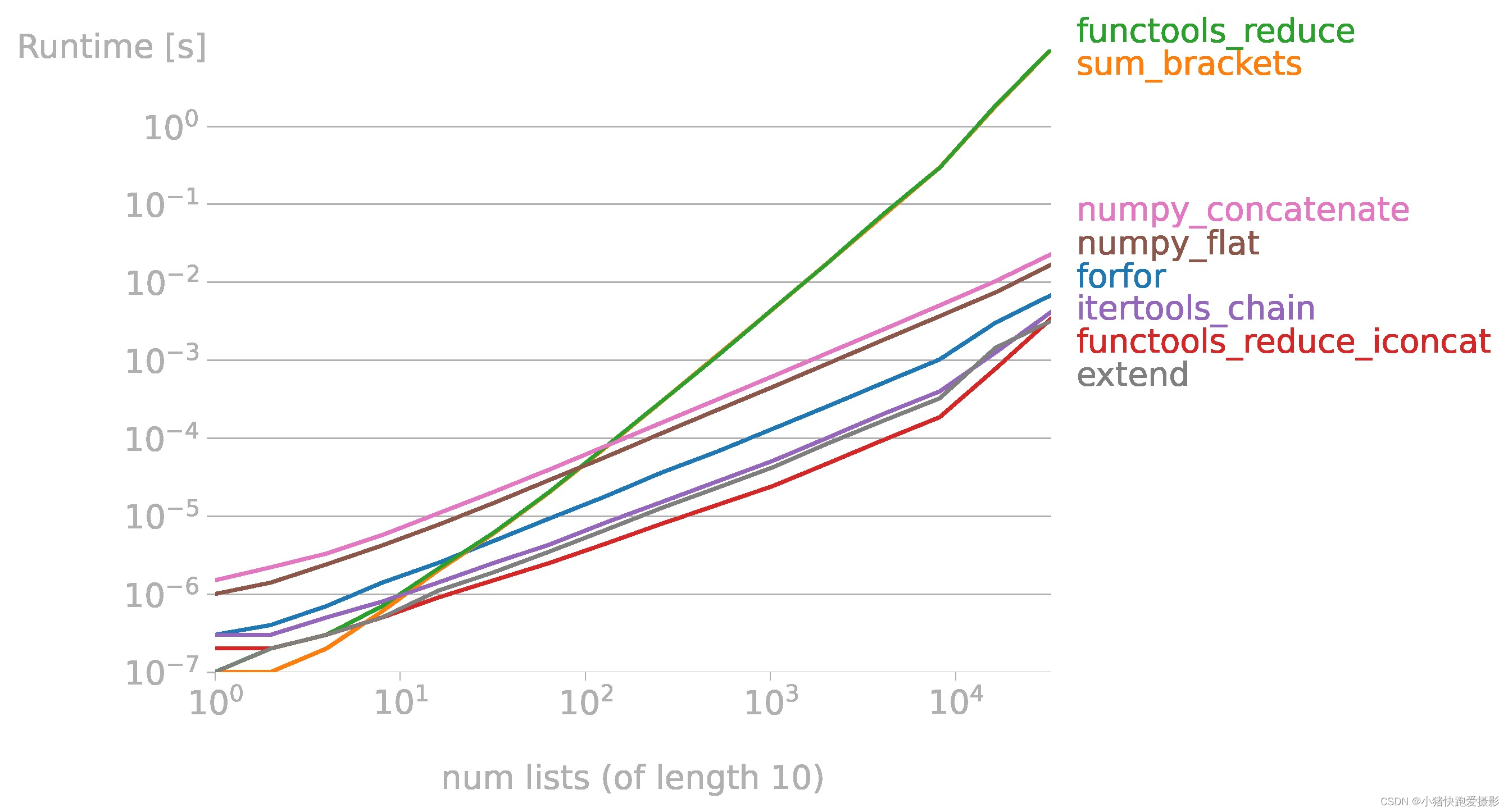
另一种是list里面的元素数量固定，增加sub-list的元素数量：

g = lambda n: [list(range(n))] * 10
g(1) = [[0], [0], [0], [0], [0], [0], [0], [0], [0], [0]]
g(3) = [[0, 1, 2], [0, 1, 2], [0, 1, 2], [0, 1, 2], [0, 1, 2], [0, 1, 2], [0, 1, 2], [0, 1, 2], [0, 1, 2], [0, 1, 2]]

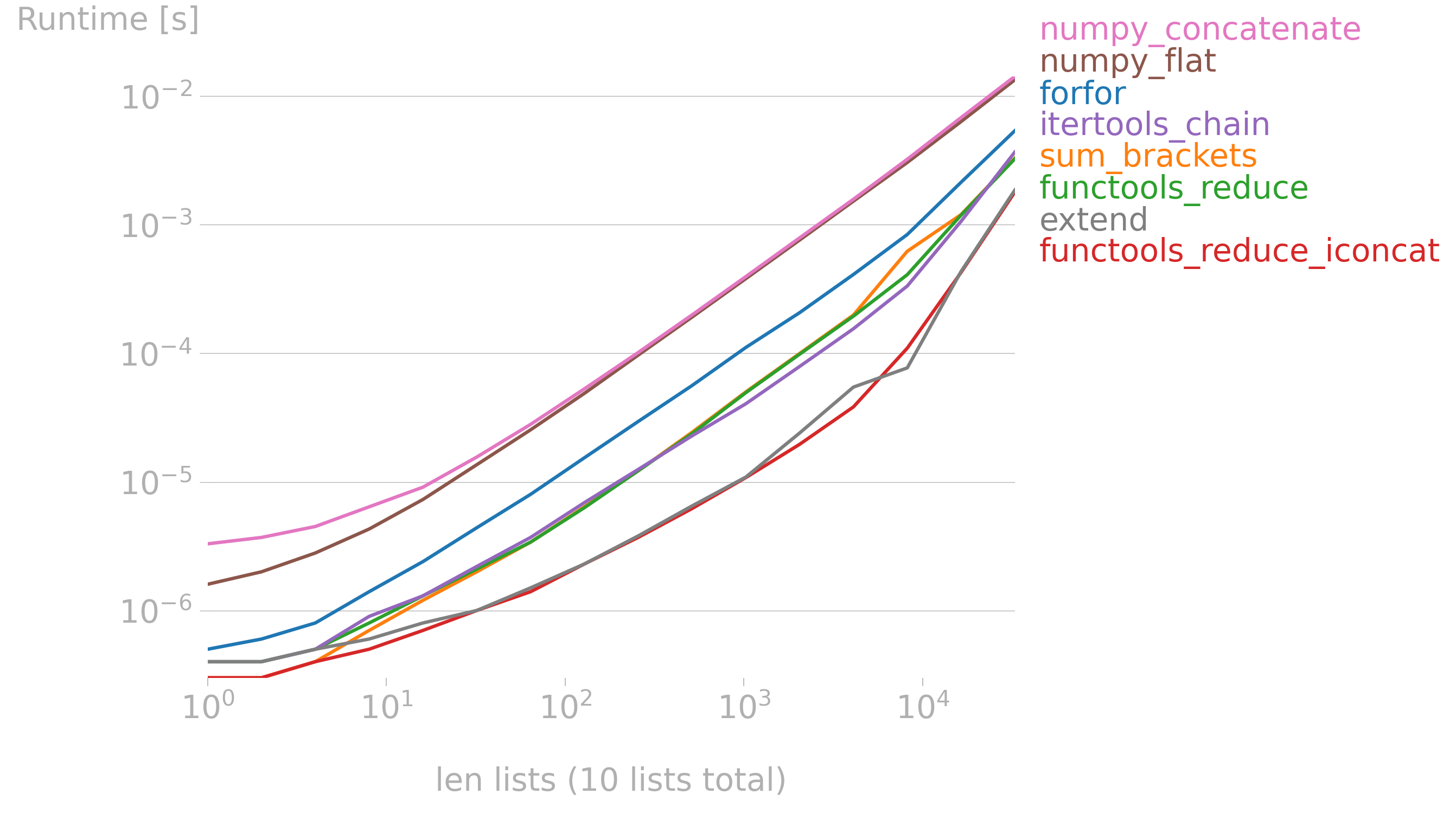
import functools
import itertools
import operator
import numpy as np
import perfplot
from matplotlib import pyplot as pltdef forfor(a):return [item for sublist in a for item in sublist]def sum_brackets(a):return sum(a, [])def functools_reduce(a):return functools.reduce(operator.concat, a)def functools_reduce_iconcat(a):return functools.reduce(operator.iconcat, a, [])def itertools_chain(a):return list(itertools.chain.from_iterable(a))def numpy_flat(a):return list(np.array(a).flat)def numpy_concatenate(a):return list(np.concatenate(a))def extend(a):out = []for sublist in a:out.extend(sublist)return outb = perfplot.bench(setup=lambda n: [list(range(10))] * n,# setup=lambda n: [list(range(n))] * 10,kernels=[forfor,sum_brackets,functools_reduce,functools_reduce_iconcat,itertools_chain,numpy_flat,numpy_concatenate,extend,],n_range=[2 ** k for k in range(16)],xlabel="num lists (of length 10)",# xlabel="len lists (10 lists total)"
)plt.figure(dpi=300)
b.save("out.png")
b.show()

在numpy数组上映射函数的最有效方法

我们有numpy数组，期望对每个元素做同样的函数操作

import numpy as np x = np.array([1, 2, 3, 4, 5])# Obtain array of square of each element in x
squarer = lambda t: t ** 2
squares = np.array([squarer(xi) for xi in x])

如果你试图向量化的函数已经被向量化了（就像上面的x**2例子），那么使用它比其他任何东西都快得多（注意对数比例）：

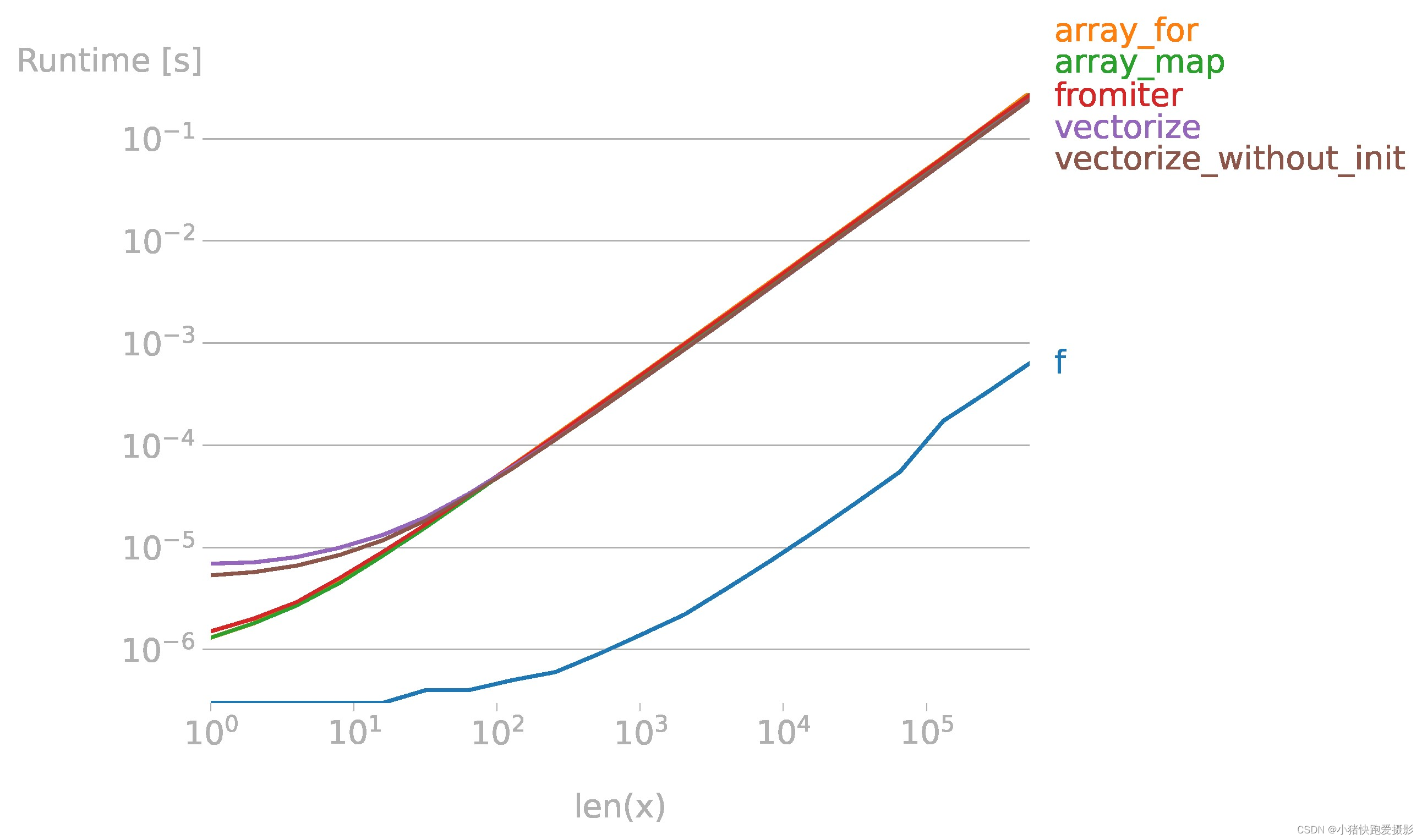
import numpy as np
import perfplot
import mathfrom matplotlib import pyplot as pltdef f(x):# return math.sqrt(x)return np.sqrt(x)vf = np.vectorize(f)def array_for(x):return np.array([f(xi) for xi in x])def array_map(x):return np.array(list(map(f, x)))def fromiter(x):return np.fromiter((f(xi) for xi in x), x.dtype)def vectorize(x):return np.vectorize(f)(x)def vectorize_without_init(x):return vf(x)b = perfplot.bench(setup=np.random.rand,n_range=[2 ** k for k in range(20)],kernels=[f,array_for,array_map,fromiter,vectorize,vectorize_without_init,],xlabel="len(x)",
)plt.figure(dpi=300)
b.save("out1.png")
b.show()

数组numpy中唯一值的最有效频率计数方法

输入：

[14, 31, 27, 27, 31, 13, 14, 13]

输出：

Item frequency:
[[13  2][14  2][27  2][31  2]
]

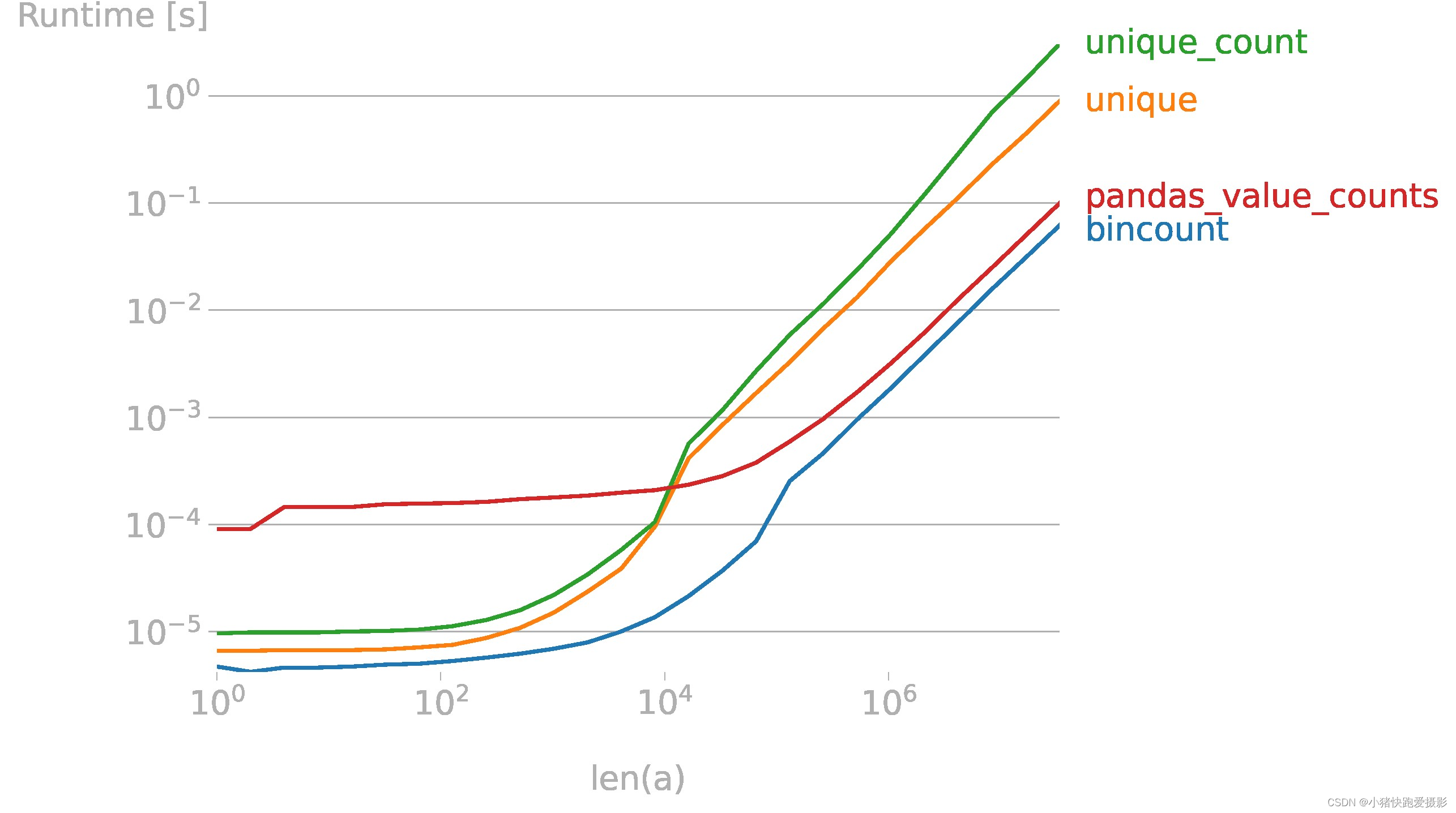
# numpy most efficient frequency counts for unique values in an array
import numpy as np
import pandas as pd
import perfplot
from matplotlib import pyplot as pltdef bincount(a):y = np.bincount(a)ii = np.nonzero(y)[0]return np.vstack((ii, y[ii])).Tdef unique(a):unique, counts = np.unique(a, return_counts=True)return np.asarray((unique, counts)).Tdef unique_count(a):unique, inverse = np.unique(a, return_inverse=True)count = np.zeros(len(unique), dtype=int)np.add.at(count, inverse, 1)return np.vstack((unique, count)).Tdef pandas_value_counts(a):out = pd.value_counts(pd.Series(a))out.sort_index(inplace=True)out = np.stack([out.keys().values, out.values]).Treturn outb = perfplot.bench(setup=lambda n: np.random.randint(0, 1000, n),kernels=[bincount, unique, unique_count, pandas_value_counts],n_range=[2 ** k for k in range(26)],xlabel="len(a)",
)
plt.figure(dpi=300)
b.save("out.png")
b.show()

反转numpy数组的最有效方法

输入：

[1, 3, 2]

输出：

[2, 3, 1]

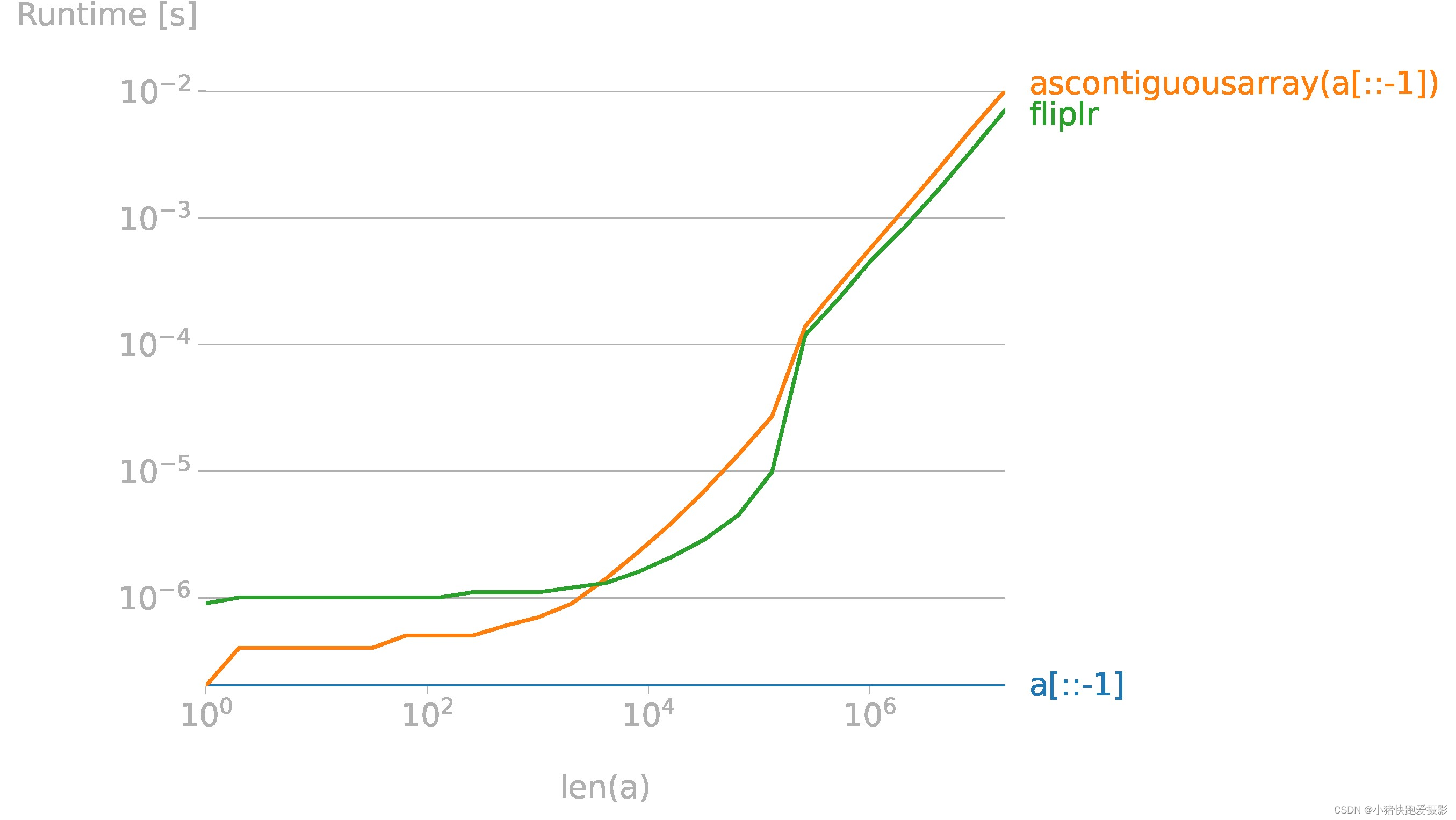
import numpy
import perfplot
from matplotlib import pyplot as pltb = perfplot.bench(setup=lambda n: numpy.random.randint(0, 1000, n),kernels=[lambda a: a[::-1],lambda a: numpy.ascontiguousarray(a[::-1]),lambda a: numpy.fliplr([a])[0],],labels=["a[::-1]", "ascontiguousarray(a[::-1])", "fliplr"],n_range=[2 ** k for k in range(25)],xlabel="len(a)",
)
plt.figure(dpi=300)
b.save('out.png')
b.show()

如何向 numpy 数组添加额外的列

输入：

[14, 31, 27, 27]

输出：

[[14, 14],[31, 31],[27, 27],[27, 27]
]

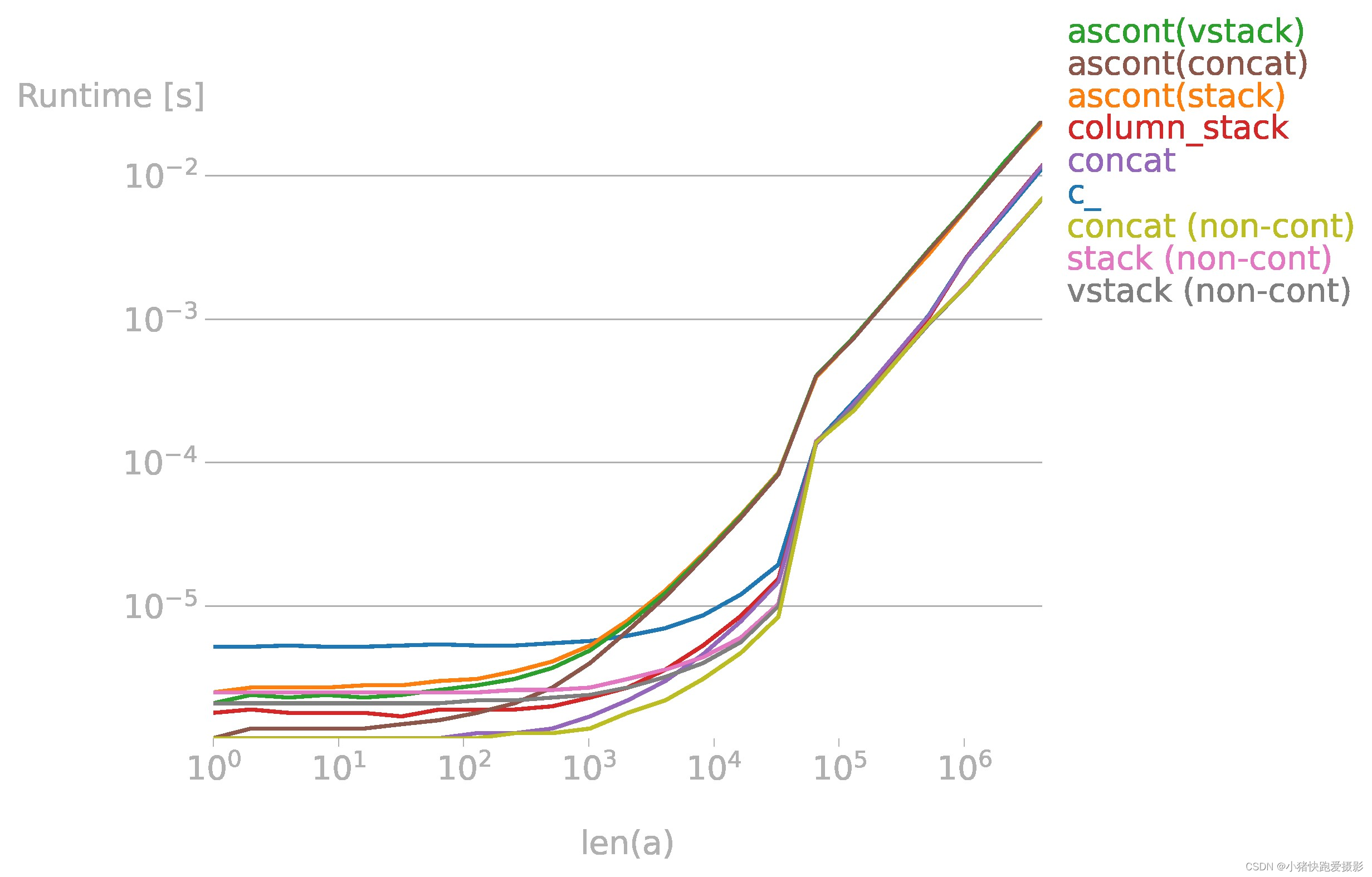
import numpy as np
import perfplot
from matplotlib import pyplot as pltb = perfplot.bench(setup=np.random.rand,kernels=[lambda a: np.c_[a, a],lambda a: np.ascontiguousarray(np.stack([a, a]).T),lambda a: np.ascontiguousarray(np.vstack([a, a]).T),lambda a: np.column_stack([a, a]),lambda a: np.concatenate([a[:, None], a[:, None]], axis=1),lambda a: np.ascontiguousarray(np.concatenate([a[None], a[None]], axis=0).T),lambda a: np.stack([a, a]).T,lambda a: np.vstack([a, a]).T,lambda a: np.concatenate([a[None], a[None]], axis=0).T,],labels=["c_","ascont(stack)","ascont(vstack)","column_stack","concat","ascont(concat)","stack (non-cont)","vstack (non-cont)","concat (non-cont)",],n_range=[2 ** k for k in range(23)],xlabel="len(a)",
)
plt.figure(dpi=300)
b.save("out.png")
b.show()

将 numpy 矩阵初始化为零或一以外的值

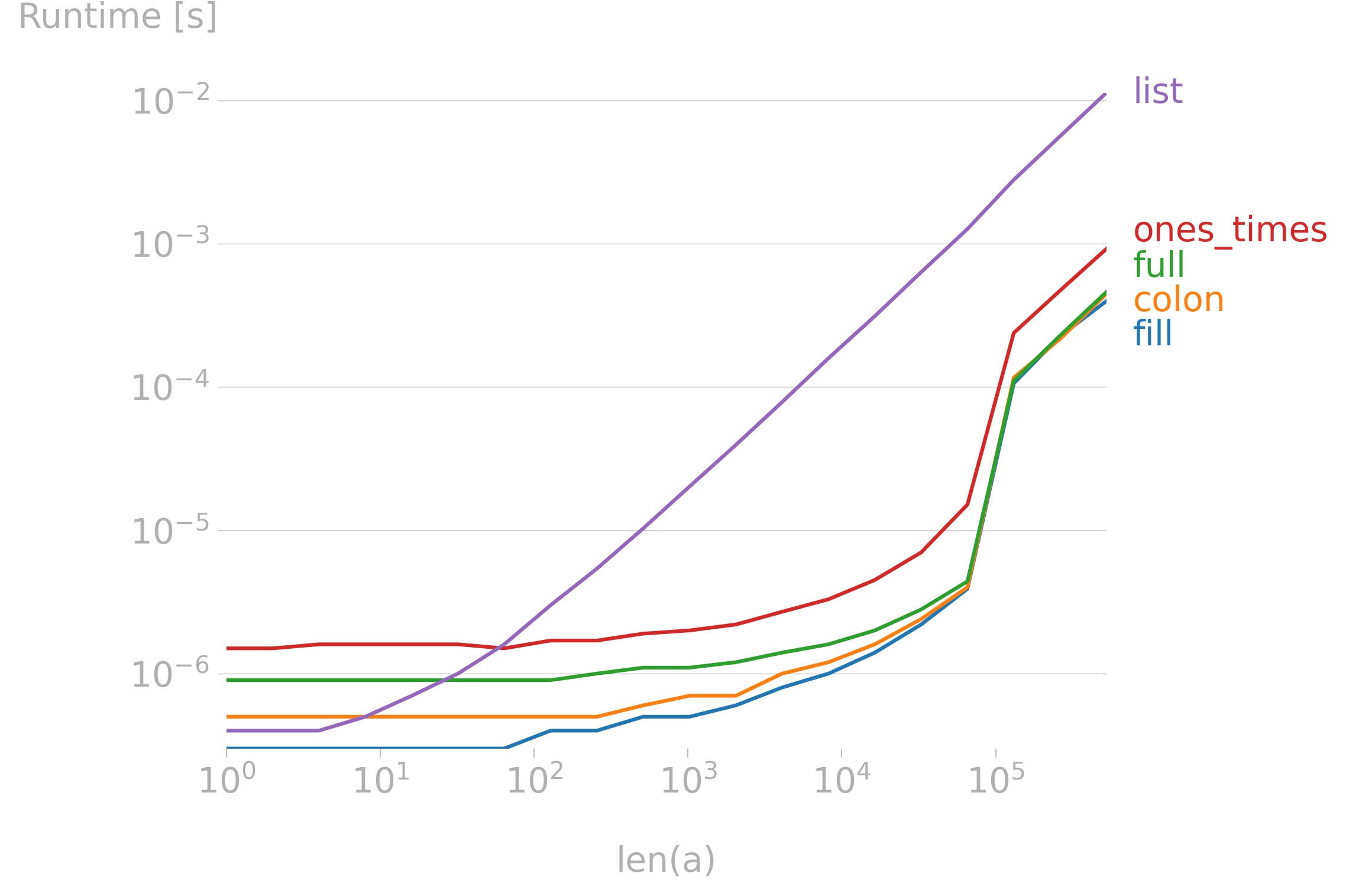
import numpy
import perfplot
from matplotlib import pyplot as pltval = 42.0def fill(n):a = numpy.empty(n)a.fill(val)return adef colon(n):a = numpy.empty(n)a[:] = valreturn adef full(n):return numpy.full(n, val)def ones_times(n):return val * numpy.ones(n)def list(n):return numpy.array(n * [val])b = perfplot.bench(setup=lambda n: n,kernels=[fill, colon, full, ones_times, list],n_range=[2 ** k for k in range(20)],xlabel="len(a)",
)
plt.figure(dpi=300)
b.save("out.png")
b.show()