宝塔+docker+jenkins部署vue项目（保姆级教程）https://blog.csdn.net/weixin_47284756/article/details/129339940

基于上述教程，不同的地方。
1.我使用的是gitee，所以需要在jenkins中安装gitee插件
配置gitee，其他默认配置就行

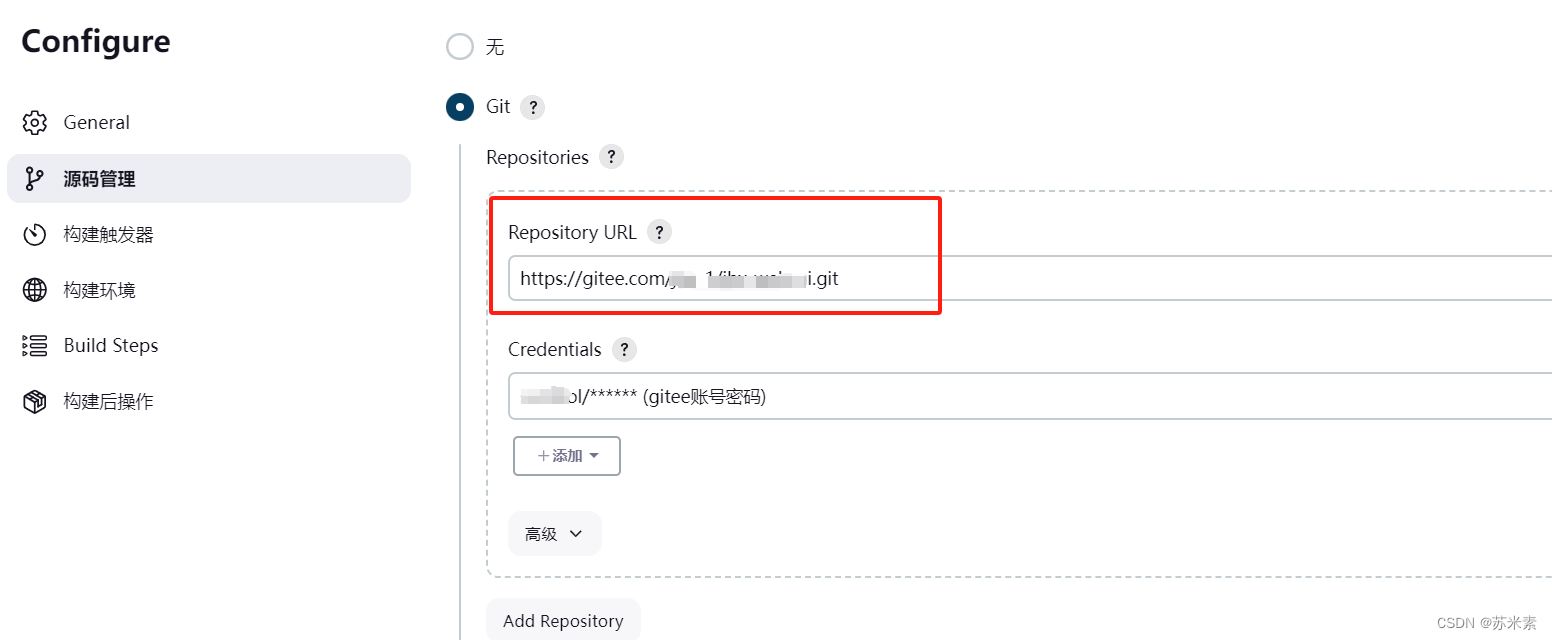
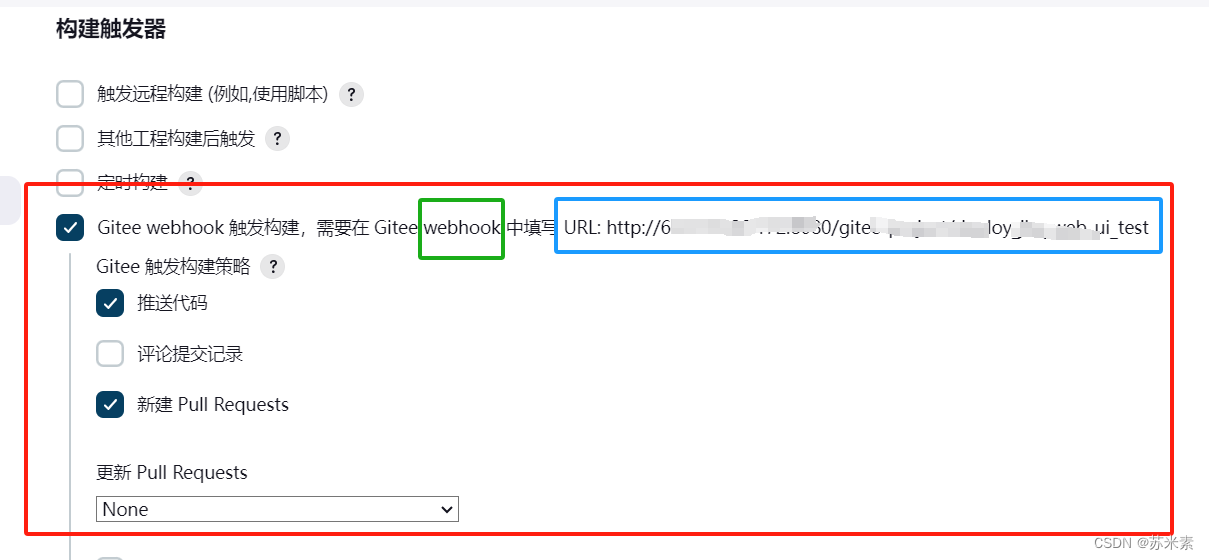
构建打包命令

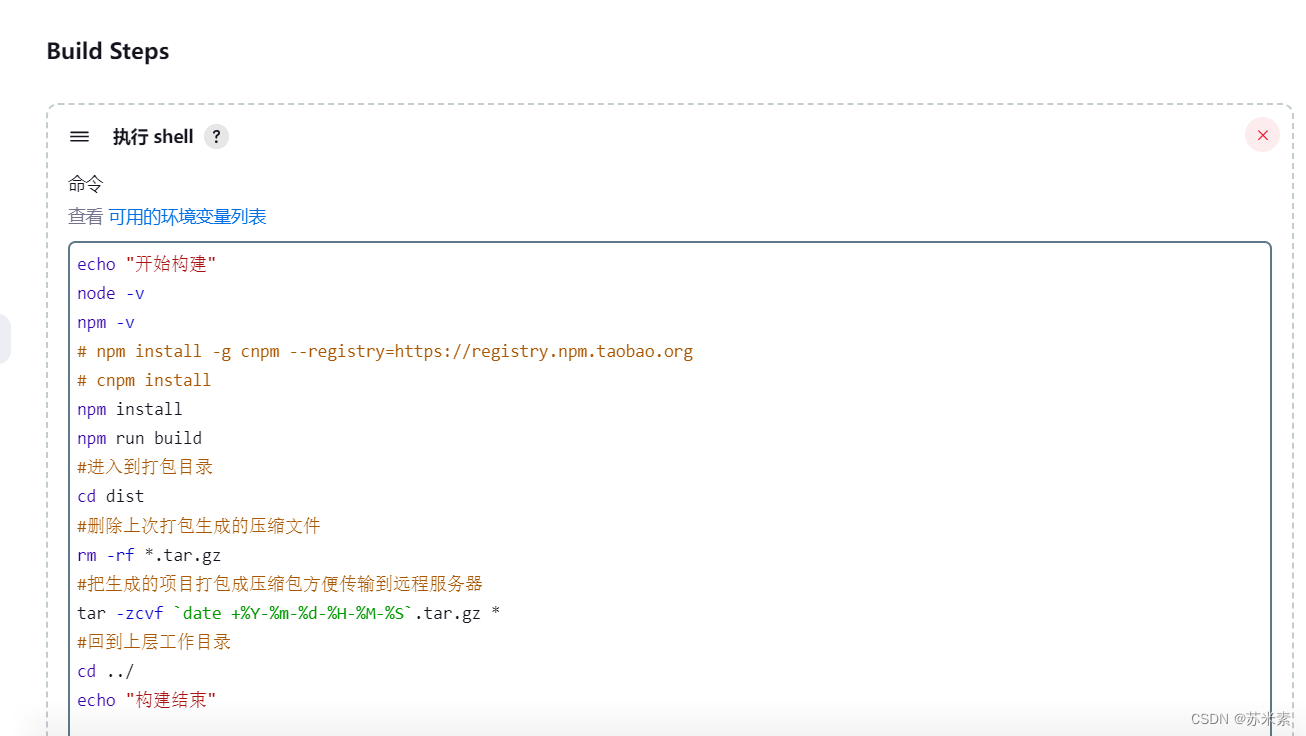
echo "开始构建"
node -v
npm -v
# npm install -g cnpm --registry=https://registry.npm.taobao.org
# cnpm install
npm install
npm run build
#进入到打包目录
cd dist
#删除上次打包生成的压缩文件
rm -rf *.tar.gz
#把生成的项目打包成压缩包方便传输到远程服务器
tar -zcvf `date +%Y-%m-%d-%H-%M-%S`.tar.gz *
#回到上层工作目录
cd ../
echo "构建结束"

像服务器发送打包后的文件-命令

#进入远程服务器的目录
cd /www/wwwroot/web/dist
#找到新的压缩包
tar -zxvf *.tar.gz -C ./
echo ">>>移除*.tar.gz"
rm -rf *.tar.gz
#发布完成
echo "发布完成"