一、概念介绍
Fisher信息量,是一次观测值所能提供的关于未知参数θ的信息量期望值的一种度量。
Fisher信息矩阵,是用利用最大似然函数估计来计算方差矩阵,表示随机变量的一个样本所能提供的关于状态参数在某种意义下的平均信息量。
Fisher信息矩阵是Fisher信息量由单个参数到多个参数情形的推广。Fisher信息量表示随机变量的一个样本所能提供的关于状态参数在某种意义下的平均信息量。费舍尔信息矩阵(FIM)是Fisher信息量的矢量化定义。
Fisher信息的主要作用是预测实验结果的准确性,主要用于实验前的设计阶段。Fisher信息越大,Score function的方差越大,代表的信息越多,对参数估计的准确度越高。<所以可以用作一种衡量指标判别模型或算法>
Fisher information的直观定义就是观测数据蕴含的信息量。
二、假设与条件
1、前提假设
假设观察到独立同分布(i.i.d)的数据 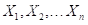 服从一个概率分布
服从一个概率分布 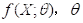 是目标参数(for simplicity, 这里
是目标参数(for simplicity, 这里 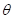 是个标量,且不考虑 nuissance parameter) , 那么似然函数 (likelihood) 就是:
是个标量,且不考虑 nuissance parameter) , 那么似然函数 (likelihood) 就是:

2、正则条件
不是所有分布都有Fisher信息量的,需要满足如下正则条件:
(1)参数空间 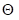 是直线上的一个开区间;
是直线上的一个开区间;
(2)支撑 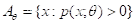 与参数
与参数 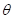 无关;
无关;
(3) 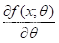 对
对 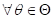 都存在;
都存在;
(4) 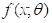 积分求导可以换序;
积分求导可以换序;
(5) 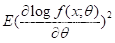 存在。
存在。
由(1)(2)可知 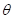 的定义域有意义;
的定义域有意义;
由(3)可知 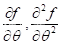 存在;
存在;
由(4)(5)可知 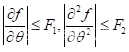 ,
, 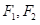 均可积。
均可积。
三、定义与性质
1、定义
似然函数的对数:

似然函数对数的一阶导数成为评分函数(Score function),性质是均值为0:

Fisher信息 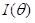 ,定义Score function的二阶矩 (second moment) :
,定义Score function的二阶矩 (second moment) :

一般情况下 (under specific regularity conditions) 可以很容易地证明,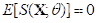 ,从而得到:
,从而得到:

Fisher信息可以通过下面公式求解:

2、最大似然估计(MLE)的渐进正态性

这里 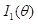 是当只观察到一个X值时的Fisher Information,当有n个 i.i.d 观测值时,
是当只观察到一个X值时的Fisher Information,当有n个 i.i.d 观测值时, 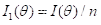 。所以这时的直观解释就是,Fisher Information反映了对参数估计的准确度,它越大,对参数估计的准确度越高,即代表了越多的信息。
。所以这时的直观解释就是,Fisher Information反映了对参数估计的准确度,它越大,对参数估计的准确度越高,即代表了越多的信息。
MLE另一个性质:当 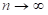 ,关于
,关于 的方程
的方程 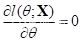 有解的概率为1。
有解的概率为1。
3、克拉默-拉奥(Cramer-Rao)方差界

克拉默-拉奥方差界是未知参数之一切可能估计量的方差的公共下界。
对于上述定义与性质,当 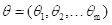 为多维时,Fisher信息矩阵为:
为多维时,Fisher信息矩阵为:

其中

这时,克拉默-拉奥方差界在多维情况下的类似: 设 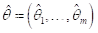 是
是 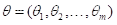 的任一无偏估计量,
的任一无偏估计量, 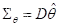 是
是 的方差矩阵,则
的方差矩阵,则 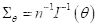 是非负定矩阵。
是非负定矩阵。
四、意义与应用
1、Fisher Information数学意义
(1)用来估计MLE的方程的方差。直观表述是,随着收集的数据越来越多,这个方差由于是一个Independent sum的形式,也就变的越来越大,也就象征着得到的信息越来越多。
(2)log likelihood在参数真实值处的负二阶导数的期望。
(3)MLE的渐进分布的方差是 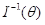 ,即
,即  。
。
(4)Fisher information 等于负对数似然的Hessian的期望,Hessian 矩阵描述了负对数似然的曲率,所以Fisher information描述了当下的似然函数能有多大的潜力寻找出最优参数。(如果似然函数很平坦,则基本找不出最大似然对应的参数。 反之,如果有尖峰,那么则表示尖峰处就是最优参数最应该存在的地方)。所以Fisher information描述了MLE的不确定度。
2、应用
经典信息几何理论将概率密度函数全体看作统计流形,用Fisher信息矩阵定义统计流形上的黎曼度量,在此基础上构建了黎曼流形。因为概率分布全体是弯曲的流形,所以可以研究各种概率分布的几何性质,例如,可以利用复希尔伯特空间上的内积可以给出类似于有限维空间上的Fisher度量和测地距离等表达式等。
Fisher信息能够指导观测。因为通过计算Fisher信息,可以知道当前观测量所包含的信息量的多少,那么也可以分析出什么情况下的观测能够包含更多的信息量,从而也就分析出了什么是好的观测。总的来说,Fisher信息的表达式可以预测估计的结果可以有多么准确。甚至在进行观测之前就能预测出这次观测能有多准确,不需要进行仿真实验,不需要知道观测的具体细节。所以可以用来评估观测的回报是否足够大,也就是说可以提前设计如何进行观测。
Fisher信息可以作为目标函数来优化,将Fisher信息作为目标函数来优化观测,通常可以得到优质的观测量。Fisher信息矩阵中的每个元素都表示的是信息量的多少,但是如果将Fisher信息作为目标函数进行优化时,需要的是一个标量的数值,此时通常情况下会选择Fisher信息矩阵的行列式作为目标函数:
参考资料:
1、费雪信息 (Fisher information) 的直观意义是什么? - 知乎
https://www.zhihu.com/question/26561604
2、【一个视频搞懂Fisher信息量(上):费歇尔信息量是什么以及相关性质的推导】
https://www.bilibili.com/video/BV1L8411W73f/?share_source=copy_web&vd_source=24db73a73cddacddda48febd1ffc28ef
3、由浅入深理解 Fisher 信息(1)——从10种不同的角度和深度理解 Fisher information - 宁子安的文章 - 知乎
https://zhuanlan.zhihu.com/p/589273267
4、百度百科
5、网络资料












)




![[数据结构]HashSet与LinkedHashSet的底层原理学习心得](http://pic.xiahunao.cn/[数据结构]HashSet与LinkedHashSet的底层原理学习心得)
)
