目录
一,回文子串
1.题目
2.题目接口
3,解题代码及其思路
解题代码:
二, 分割回文串II
1,题目
2,题目接口
3,解题思路及其代码
一,回文子串
1.题目
给你一个字符串
s,请你统计并返回这个字符串中 回文子串 的数目。回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:s = "abc" 输出:3 解释:三个回文子串: "a", "b", "c"示例 2:
输入:s = "aaa" 输出:6 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"提示:
1 <= s.length <= 1000s由小写英文字母组成
2.题目接口
class Solution {
public:int countSubstrings(string s) {}
};3,解题代码及其思路
在动态规划问题时一般可以分为五个步骤:
1.状态表示
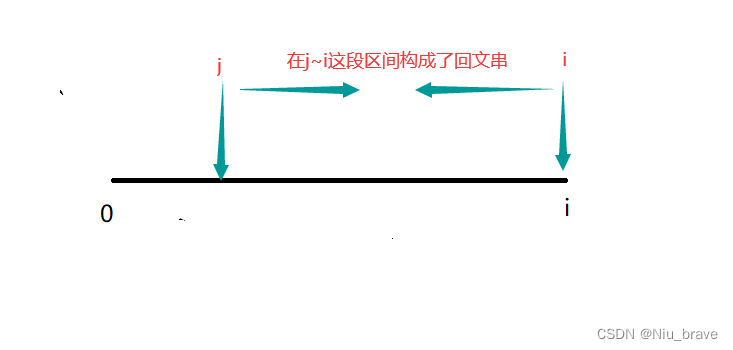
回文串问题我们一般以某一个区间为研究对象,所以我们可以使用bool dp[i][j]来表示i~j这段区间是否为回文串。
2.状态转移方程的推导
确定了状态转移方程以后,我们便可以来讨论状态转移方程。在推导状态转移方程时可以分为两种情况来推导:
1.s[i]==s[j],在这种情况下又可以分为三种情况来推导:
2.s[i]!=s[j]。在这种情况下dp[i][j]这段区间内的字符串肯定不是回文串。所以dp[i][j] = false。
3.填表顺序
因为在我们的状态转移方程内有dp[i][j] == dp[i+1][j-1]的情况,所以填表顺序为从下往上,从左往右。
4.初始化
在初始化的时候,要考虑的一个情况便是我的初始化要保证填表时不越界。dp[i][j] == do[i+1][j-1],在这种情况下因为 0<=i<=j<n。所以越界的情况在于i==n-1的时候,dp[i+1][j-1]会越界。但是我们要考虑这种情况吗?我们其实并不需要,因为j>=i,当i==j时会直接处理:dp[i][j] =true,并且只在这种情况下会越界。
5.返回值
在完成上面的工作以后,只需要完成对dp[i][j]中true情况的个数统计并返回。
解题代码:
class Solution { public:int countSubstrings(string s) {int n = s.size();//求字符串长度vector<vector<bool>>dp(n,vector<bool>(n));//建立n*n大小的dp表for(int i = n-1;i>=0;i--)//从下往上遍历{for(int j = i;j<n;j++)//从左到右遍历并且要保证j>=i{if(s[i] == s[j])//相等情况讨论{if(i == j) dp[i][j] = true;else if(j == i+1) dp[i][j] = true;else dp[i][j] = dp[i+1][j-1];}//s[i]!=s[j]时dp[i][j]绝对是false}}//统计回文子串个数int count = 0;for(int i = 0;i<n;i++){for(int j = i;j<n;j++){if(dp[i][j]) count++;}}return count;} };
二, 分割回文串II
1,题目
给你一个字符串
s,请你将s分割成一些子串,使每个子串都是回文。返回符合要求的 最少分割次数 。
示例 1:
输入:s = "aab" 输出:1 解释:只需一次分割就可将 s 分割成 ["aa","b"] 这样两个回文子串。示例 2:
输入:s = "a" 输出:0示例 3:
输入:s = "ab" 输出:1提示:
1 <= s.length <= 2000s仅由小写英文字母组成
2,题目接口
class Solution {
public:int minCut(string s) {}
};3,解题思路及其代码
还是一样,按照之前的五个步骤:
1,状态方程:这次的状态转移方程表示的是分割回文串的最小次数。所以我们可以用一个线性的dp表来表示,用dp[i]表示0~i位置的最小切割次数。
2,状态转移方程:在确定好状态转移方程以后,我们就得来推导一下状态转移方程了。还是得分情况讨论:
在第一种情况下,因为0~i这个区间的字符可以构成回文串了所以dp[i] = 0。
在第二种情况下,需要在1~i这个区间内寻找一个能让dp[j][i]构成回文串的并且让切割次数最
最小:
在进行这一步以前还得分情况讨论:
状态转移方程代码如下:
for(int i = 0;i<n;i++){if(dp[0][i]){dp2[i] = 0;}else{for(int j =1;j<=i;j++){if(dp[j][i]) {dp2[i] = min(dp2[i],dp2[j-1]+1);}} }}3.初始化
因为我们要求的是最小值,所以我们在初始化时可以把状态表内的值初始化为一个特别大的值,这样便可以保证在我们填表时不会干扰到我们的在正确答案。
4,返回值
因为dp表代表的是到第i个位置的最小切割次数,所以我们的返回值就是dp[n-1]。
5,优化
因为在填表总是需要判断是否能构成回文串,所以我们可以采用判断回文子串的代码来对我们的代码做优化处理。
详细代码如下:
class Solution { public:int minCut(string s) {int n = s.size();//求字符串长度vector<vector<bool>>dp(n,vector<bool>(n));//建立n*n大小的dp表for(int i = n-1;i>=0;i--)//从下往上遍历{for(int j = i;j<n;j++)//从左到右遍历并且要保证j>=i{if(s[i] == s[j])//相等情况讨论{if(i == j) dp[i][j] = true;else if(j == i+1) dp[i][j] = true;else dp[i][j] = dp[i+1][j-1];}//s[i]!=s[j]时dp[i][j]绝对是false}}vector<int>dp2(n,0x7777777);//统计到第i个位置时的最小分割次数for(int i = 0;i<n;i++){if(dp[0][i]){dp2[i] = 0;}else{for(int j =1;j<=i;j++){if(dp[j][i]) {dp2[i] = min(dp2[i],dp2[j-1]+1);}} }}return dp2[n-1];} };




:函数模板的匹配原则,类模板的实例化)










预习报告)


 输出格式备查)


)
)
的计算方法与源程序)