一、选择题(每空 1 分,共 5 分)
1、下面关于图的叙述中,正确的是( )。
(1).回路是简单路径
(2).存稀疏矩阵,用邻接矩阵比邻接表更省空间
(3).若有像图中存在拓扑序列,则该图不存在回路
A.仅(2) B.仅(1)(2) C.仅(3) D.仅(1)(3)
2、在一个图中,所有顶点的度数之和等于图的边数之和的( )倍。
A.1/2 B.2 C.1 D.4
3、在一个有向图中,所有顶点入度之和与所有顶点出度之和的比是( )。
A.1/2 B.2 C.1 D.4
4、如果从无向图的任意一个顶点出发,进行一次深度优先搜索可以访问到图中所有的顶
点,则该图一定是( )。
A.有向图 B.强连通图 C.非连通图 D.连通图
5-1、深度优先遍历,类似于二叉树的( )(0.5 分)。
A.先序遍历 B.中序遍历 C.后续遍历 D.层次遍历
5-2、广度优先遍历,类似于二叉树的( )(0.5 分)。
A.先序遍历 B.中序遍历 C.后续遍历 D.层次遍历
二、简答题(共 15 分)
1、使用迪杰斯特拉(Dijkstra)算法求下图 1 中从顶点 1 到其他各顶点的最短路径,请给出依 次得到的各最短路径的目标顶点结果【推导出从顶点 1 出发各个顶点的正确的最短路径结果即 可,注意推导过程中的次序】。(5 分)

2、有图 2 所示的无向网,请分别给出:(1)邻接矩阵;(2)邻接表;(3)最小生成树(Prim 算法、Kruskal 算法)。(5 分)

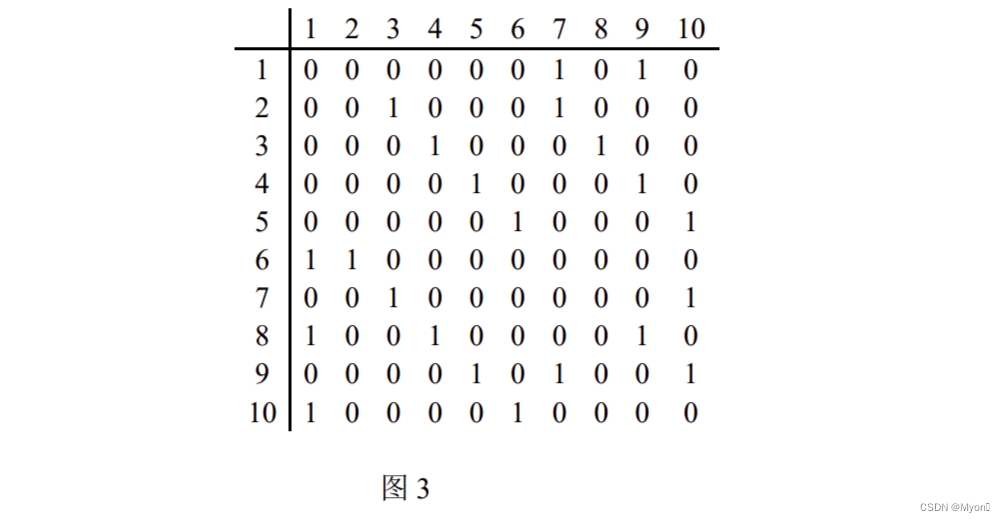
3、已知图 3 所示的邻接矩阵,请画出自顶点 1 出发遍历得出的广度优先生成树。(5)分







畅捷通的 Serverless 探索实践之路)

)
:初识nodejs、模块化、CommonJS、ESModule等)








使用说明书(五,轻量级的visionpro))