日前价格预测
预测说明：
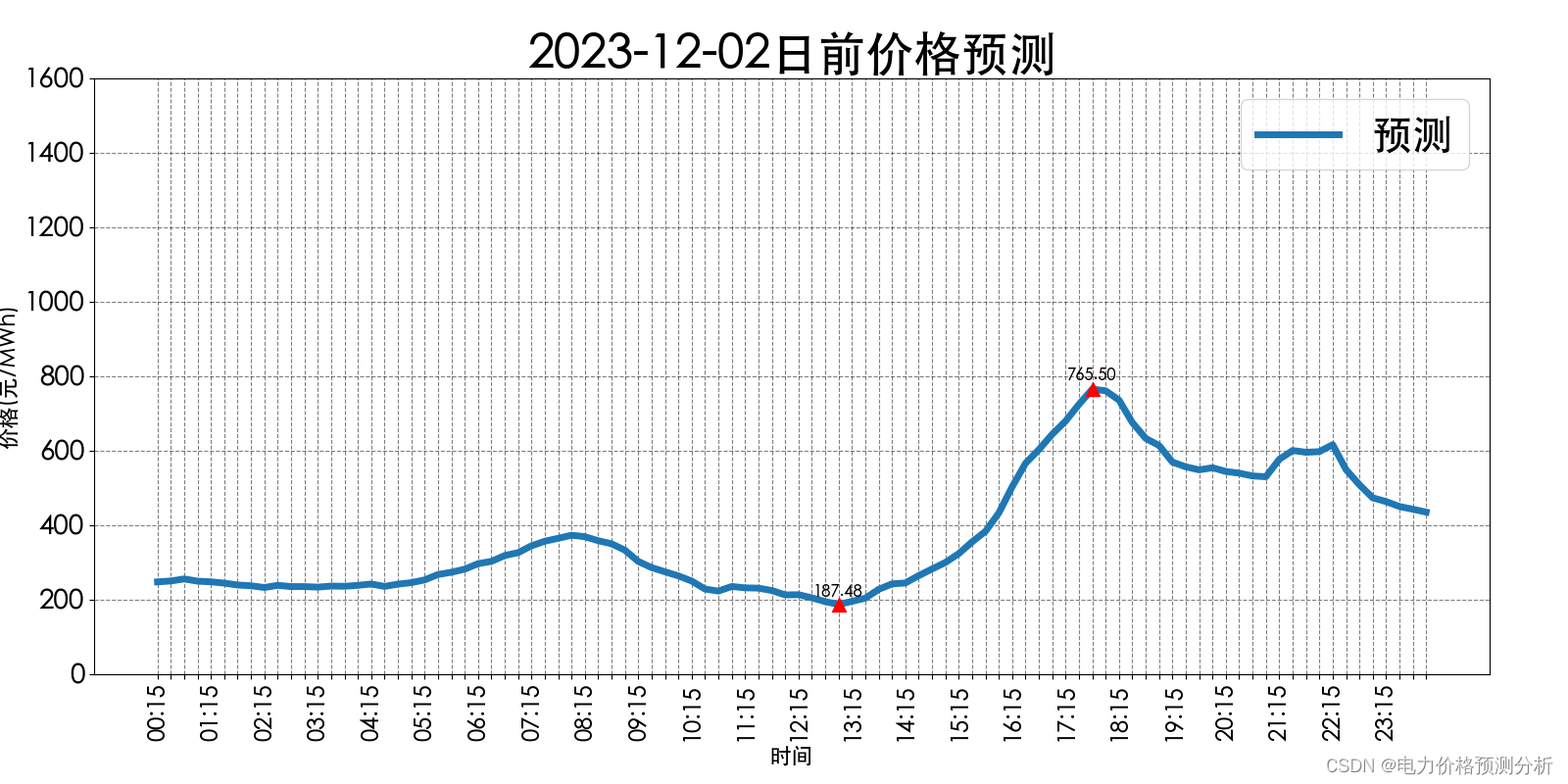
如上图所示，预测明日（2023-12-02）山西电力市场全天平均日前电价为373.22元/MWh。其中，最高日前电价为765.50元/MWh，预计出现在17:45。最低日前电价为187.48元/MWh，预计出现在13:00。
以上预测仅供学习参考，严禁用于商业用途。
价差方向预测
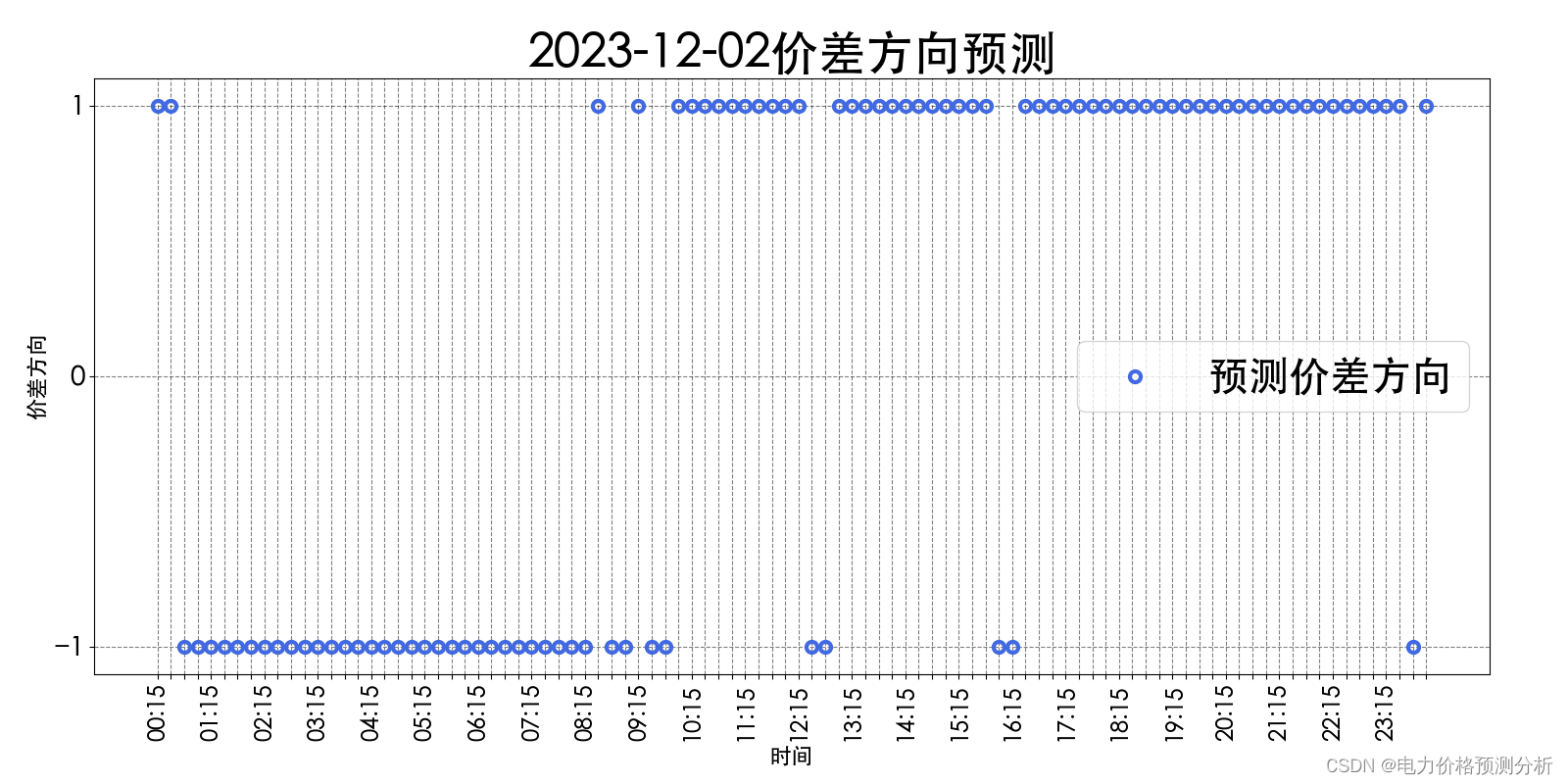
上图价差方向预测的补充说明：
纵坐标数值为 1 表示的价差方向是： 实时价格 > 日前价格
纵坐标数值为 0 表示的价差方向是： 实时价格 = 日前价格
纵坐标数值为 -1 表示的价差方向是：实时价格 < 日前价格
注：价差代表的是原始出清价格的价差，并非最终结算价格的价差。
以上预测仅供学习参考，严禁用于商业用途。
昨日日前价格预测回顾
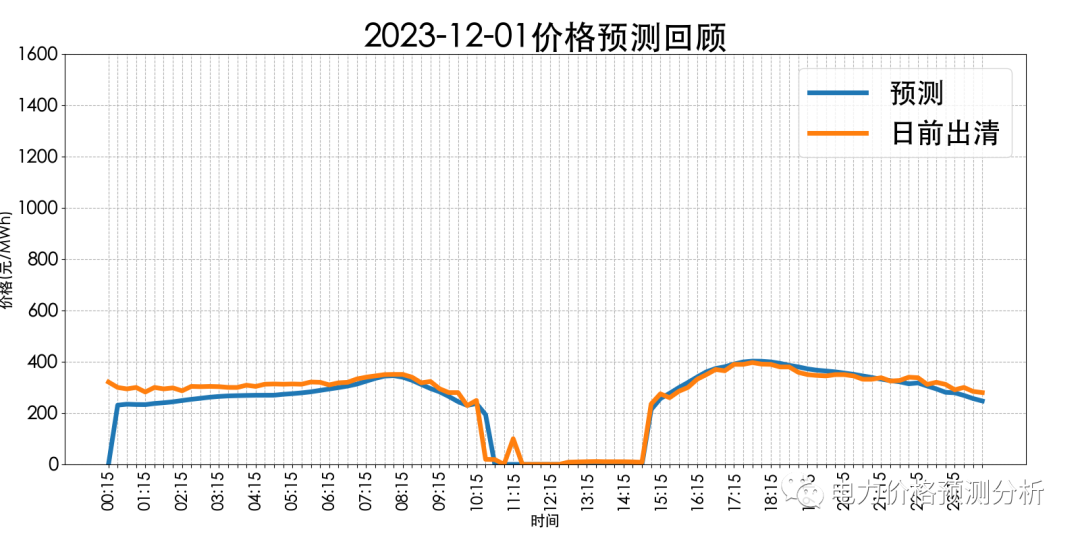
预测结果分析：
如上图所示，昨日(2023-12-01) 全天96个点平均预测准确率90.04%，平均绝对偏差为26.17元/MWh。最大偏差为321.00元/MWh,出现在0:15。最小偏差为0.00元/MWh,出现在11:00,11:30~12:30。
价差方向预测回顾
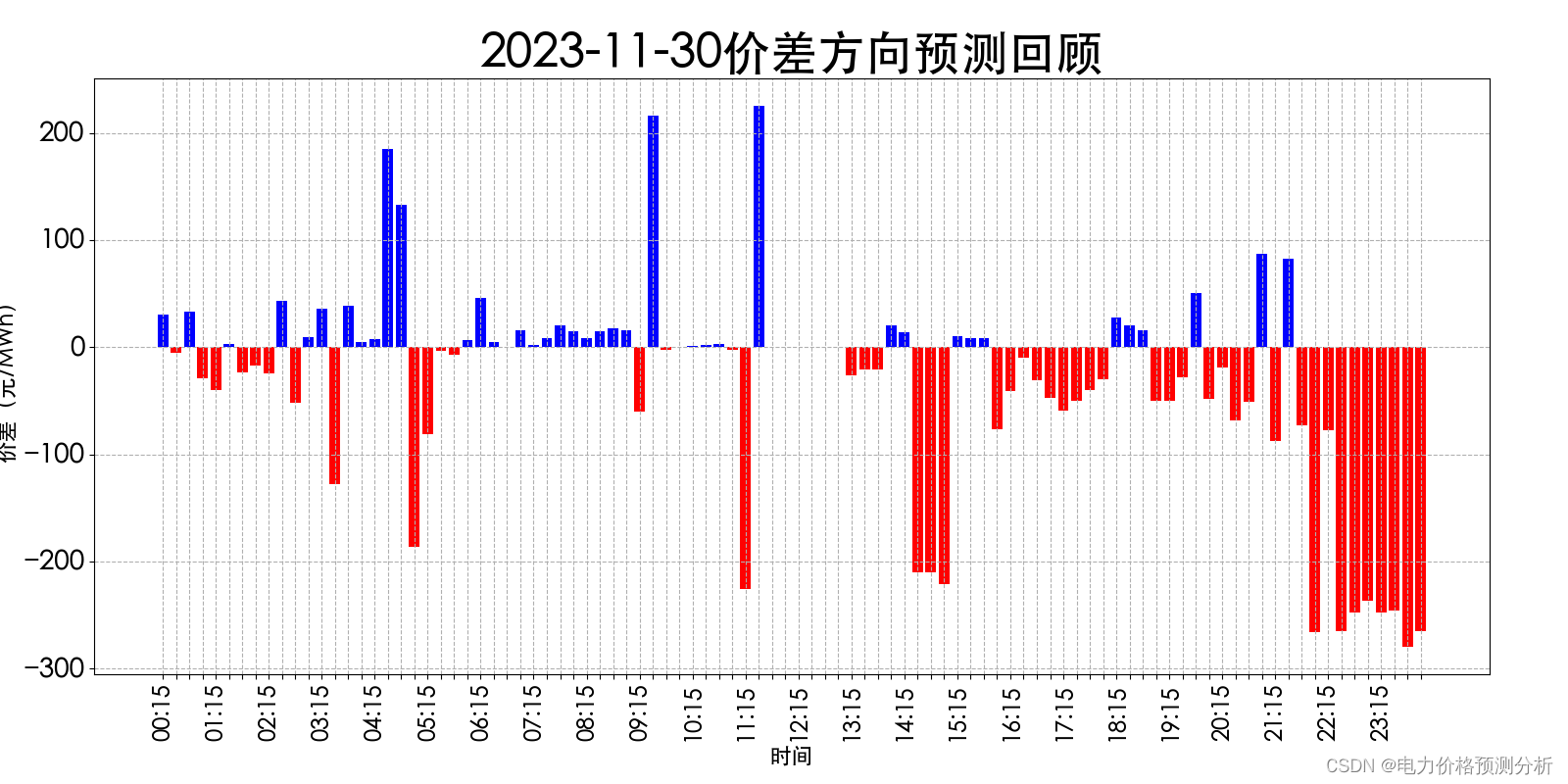
上图价差方向预测回顾图说明：
蓝色柱状图表示：该时段预测价差方向与实际价差方向一致。
红色柱状图表示：该时段预测价差方向与实际价差方向相反。
预测结果分析：
2023-11-30 全天96个时段价差方向预测准确率：-50.9%
