备战春招——12.1 算法

动态规划

动态规划的核心思想就是本次只由上一次决定。

爬楼梯

在这里插入图片描述
第3阶由（第1节+2）和（第二节+1），不要想着往下迭代，不然那是个无穷底。所以f(x)=f(x-1)+f(x-2) (x>2)。所以就是当前只与上个操作相关。

class Solution {
public:int climbStairs(int n) {if(n==1) return 1;if(n==2) return 2;int a = 1; //f(x-2)int b = 2; //f(x-1)int sum = a+b;for(int i=4;i<=n;i++){a = b;      //更新f(x-2)  b =sum;     //更新f(x-1)sum = a+b;  //f(x) = f(x-1)+f(x-2)}return sum;}
};

杨辉三角

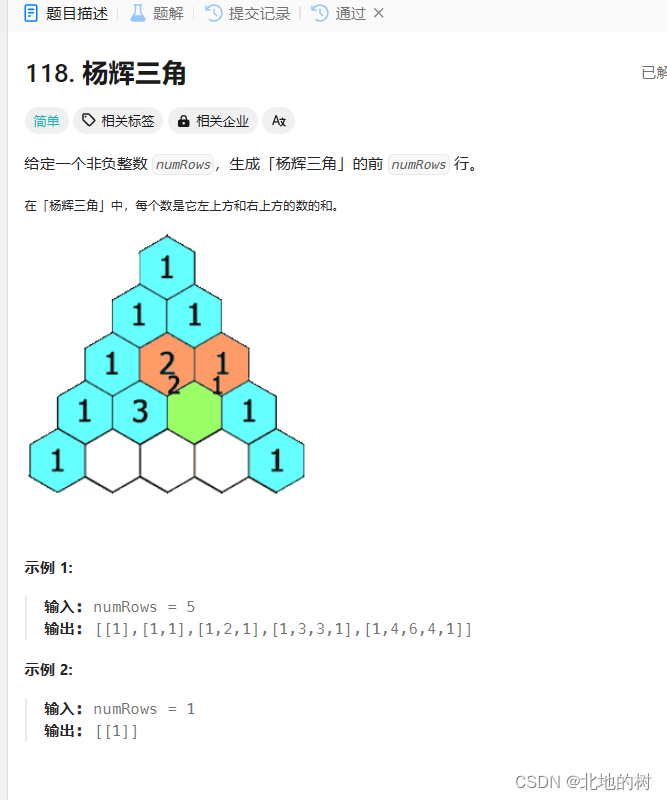
在这里插入图片描述
动态规划，还是写出哪个公式嘛，主要是控制好循环那个i层数字索引。

class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>> data;if(numRows==0) return data;//f(n)(m)=f(n-1)(m-1)+f(n-1)(m)  差不多就是这个了吧，每组第一个和最后一个都是1vector<int>  d;d.push_back(1);data.push_back(d);for(int i=1;i<numRows;i++){vector<int> d;d.push_back(1);for(int j=1;j<i;j++){//f(n)(m)=f(n-1)(m-1)+f(n-1)(m)  差不多就是这个了吧，每组第一个和最后一个都是1d.push_back(data[i-1][j-1]+data[i-1][j]);}d.push_back(1);data.push_back(d);}return data;}
};

杨辉三角2

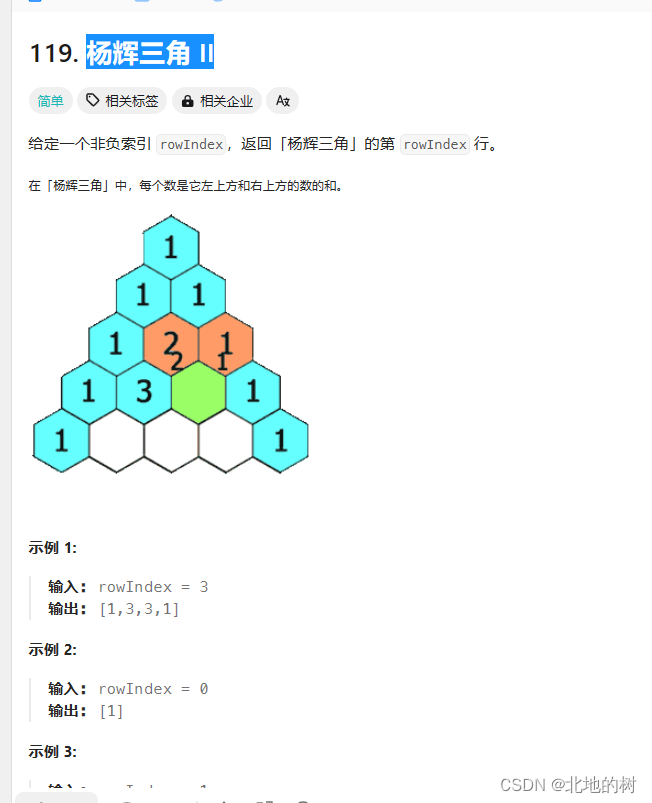
在这里插入图片描述

what up。 swap(vector1,vector2);可以替换两个，这么爽吗。

class Solution {
public:vector<int> getRow(int rowIndex) {vector<int>  d;vector<int> data;if(rowIndex == 0) {d.push_back(1);return d;}for(int i=1;i<=rowIndex;i++){swap(data,d);   //可以直接转换哈data.clear();    //清空当前需要返回的数据。data.push_back(1);for(int j=1;j<i;j++){data.push_back(d[j-1]+d[j]);  //f(n)(m) = f(n-1)(m-1)+f(n-1)(m);}data.push_back(1);}return data;}
};

买卖股票的最佳时机

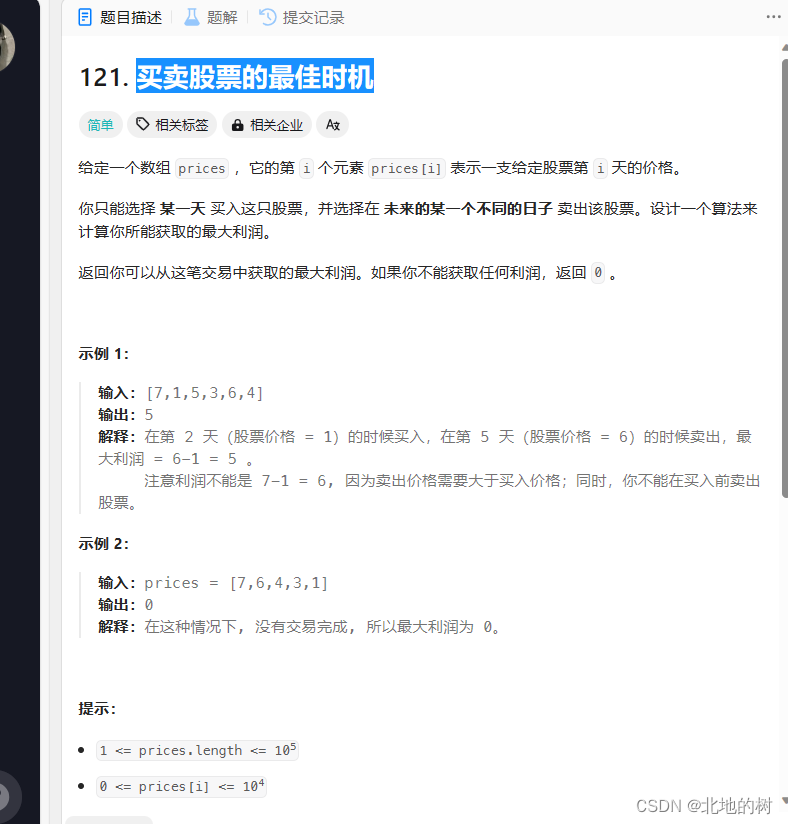
在这里插入图片描述
一遍遍历,mindp[i]=min(dp[i-1],price[i]) 这里面动态规划的是最小的价格，然后再计算最大的利润，不是直接的动态规划东西。

class Solution {
public:int maxProfit(vector<int>& prices) {//一次遍历，寻找前面的最小值，一遍扫描，然后寻找maxprofix//dp(x)=min(),然后去计算最大利润，也就是前面的最值。vector<int> dp(prices.size(),0);int max = 0;dp[0] = prices[0];for(int i=1;i<prices.size();i++){if(max<(prices[i]-dp[i-1])){max = (prices[i]-dp[i-1]);}dp[i] = min(dp[i-1],prices[i]);}return max;}
};

比特位计数

在这里插入图片描述
最高位有效，mod2为0或者1，如果除以2为0的话，表示是一样的1数字。如果余数为1的话，需要+1。

class Solution {
public:vector<int> countBits(int n) {//动态规划。//最高或者最低位有效位，其实就是找比上前一个多一个1的vector<int> data(n+1,0);data[0]=0;if(n==0) return data;data[1]=1;for(int i=2;i<=n;i++){if(i%2==0) data[i]=data[i/2];if(i%2==1) data[i]=data[i/2]+1;}return data;}
};