理解递归
一、递归的特征
1.执行范围不断缩小
递归类似数学里的递推,设计递归就是努力寻找数学里的递推公式,例如阶乘的递推公式就是f()=n*f(n-1),很明显一定是要触底之后才能反弹。再比如斐波那契数列的递归公式为f(n)=f(n-1)+f(n-2),n也在不断缩小。这条规律可以辅助我们检查自己写的递推公式对不对。
2.终止条件在递归调用的前面
递归之后可能还有终止条件,但是在执行递归之前,一定会有一个终止条件。这一条也可以帮助我们检查自己写的算法对不对。
如果递归之前没有终止条件,递归就会一直进行下去。
二、写递归
第一步、从小到大递归
可以从n==1开始考虑递归关系,然后让n逐渐增大,判断递归关系是否成立。在算法里,我们写递归一般不需要证明,先选几个较小的值验一下,再选择几个比较大的验一下即可。
第二步、分情况讨论,明确结束条件
我们说过递归里终止条件一定是靠前的,而大部分递归的终止条件不过是最小开始触底反弹时的几种情
况。
对于阶乘,当n=1时你就应该知道f(1)=1,也就是下面这样子:

有时候需要考虑的终止条件不止一个,例如斐波那契数列的递推公式f(n)=f(n-1)+f(n-2)里,如果n=2时会出现(2)=f(1)+f(0),很明显这里是没有f(0)的,所以我们要将==2也给限制住,所以结束条件是这样的:

有些情况不一定是触底才开始反弹,而是达到某种要求就要停止,这样需要考虑的情况会比较多。解决这类问题最直接的方式就是枚举,将可能的情况列举一下,再逐步优化。
确定终止条件对于递归至关重要,后面很多题目会花很大的篇幅来分析怎么判断终止条件,而一旦判断完毕,递推关系也就水到渠成了。
第三步、组合出完整方法
将递推公式和终止条件组合起来,变成完整的方法。
递归经常能看到很多骚操作代码,不要迷信这些,先分情况逐个先写出来,之后再看能否精简优化,不要步子太大。
三、看懂递归
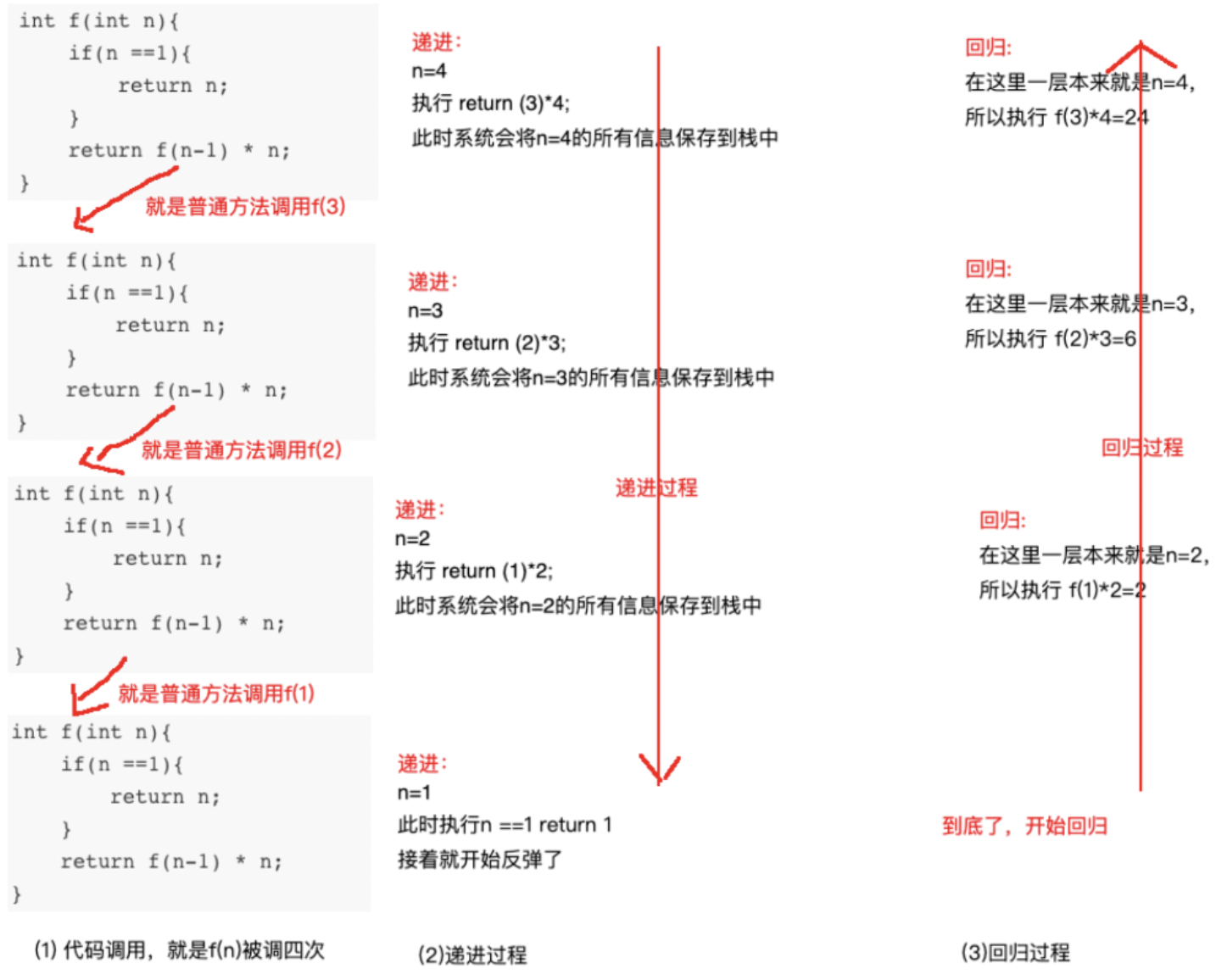
以f(4)阶乘为例
:IDEA安装)


















使用说明书(三,轻量级的visionpro))