[数据结构]深入浅出讲解二叉树-平衡二叉树-左右旋转
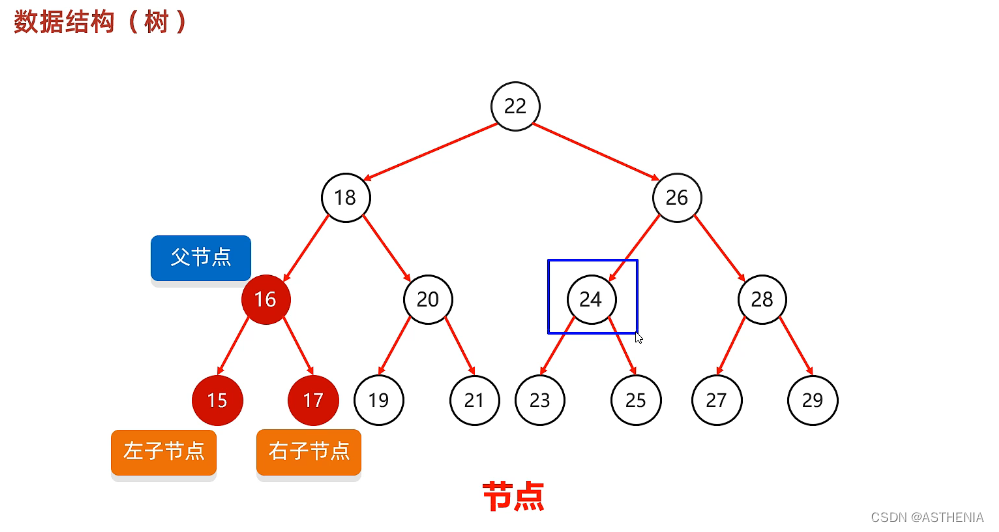
树->数据结构:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/188824.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Java面向对象第九天
精华笔记: 多态:多种形态 意义: 同一个对象被造型为不同的类型时,有不同的功能------所有对象都是多态的 ----对象多态:我、你、水...... 同一类型的引用指向不同的对象时,有不同的实现------所有抽象方法…
uniapp-从后台返回的一串地址信息上,提取省市区进行赋值
1.这是接口返回的地址信息 2.要实现的效果 3.实现代码: <view class"address">{{item.address}}</view>listFun() {let url this.$url.url.positionInfoCompany;let param {page: this.page,limit: this.limit,keyword: this.keyword,};thi…
系统部署安装-Centos7-系统常用工具安装
文章目录 Yum环境安装介绍安装 GCC安装介绍验证安装在线安装离线安装 Yum环境安装
介绍
Yum是Centos操作系统中的一个重要工具,它可以帮助用户方便地管理软件安装和更新,而Y源则是提供这些软件的资源库。在后续在线安装系统时,需要使用到Yu…
大数据(十二):方差分析和参数估计
专栏介绍
结合自身经验和内部资料总结的Python教程,每天3-5章,最短1个月就能全方位的完成Python的学习并进行实战开发,学完了定能成为大佬!加油吧!卷起来!
全部文章请访问专栏:《Python全栈教程(0基础)》 再推荐一下最近热更的:《大厂测试高频面试题详解》 该专栏对…
服务器环境是什么意思?
服务器环境是指运行在服务器上的软件和硬件配置的组合。它包括操作系统、服务器软件、数据库、编程语言解释器、网络配置以及其他必要的组件和设置。
服务器环境的配置对于应用程序的运行和性能至关重要。以下是一些常见的服务器环境组件: 操作系统:服务…
应用于智慧金融的AI边缘计算盒子+AI算法软硬一体化方案
传统金融营业厅存在运营管理模式落后、资源投放不平衡、从业人员培训效果不达预期、客户体验割裂等普遍现象; 部署英码数字金融解决方案,将助力企业从传统金融模式快速向数字金融模式转变,可针对每一个客户定制个性化“一对一”服务ÿ…
基于springboot+vue的点餐系统(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…
【23真题】耗时一周还原,终于有真题啦!
今天分享的是23年上海电力850的信号与系统回忆版试题及解析。上电的真题资源极其稀少,去年我找了3份,全部为假!好在今年有刚刚上岸的同学全力协助,为大家弄出一份回忆版真题,希望对大家有帮助!
小马哥Tips…
HarmonyOs 4 (二) HelloWord
目录 一 开发工具下载安装1.1 下载安装包1.2 下载相关依赖 二 开发者注册与个人实名认证三 第一个程序2.1 创建第一个程序2.2 认识开发者界面2.3 目录结构认识2.3.1 父目录认识2.3.2 AppScope 目录2.3.3 entry目录2.3.3.1 ets 目录2.3.3.2 resources目录 2.3.4 认识配置文件2.3…
UE中记:静默自更新插件(多路径部署
自动更新系统原理说明文档
概述
本自动更新系统是一个基于Node.js的应用程序,用于自动检查、下载、解压并安装软件更新。它由多个脚本和一个更新服务器组成,能够在后台自动执行更新流程,确保软件保持最新状态。
组件说明
SetUp.bat: 主批…
Halcon 螺丝孔位定位
标定坐标:对整个9点标定版进行拍摄时的世界坐标HomMat2D1:标定后得到的换算关系孔位世界坐标:相机移动到孔位上的世界坐标圆心世界坐标:模版匹配后得到的螺丝孔位中心
相对偏移: 孔位世界坐标 - 标定坐标 目标坐标:圆…
【LeetCode】 160. 相交链表
相交链表 题目题解 题目
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交: 题目数据 保证 整个链式结构中不存在环。
注意&am…
FileInputStream 与 FileOutputStream
IO流:存贮和解决数据的存储方案 以上都是抽象类,不能创建实例 FileOutputStream
操作本地的文件,把文件写入本地磁盘
步骤: 1.创建字节输出流对象 参数是字符串表示的路径或者是File对象都是可以的如果文件不存在会创建一个新的…
redis笔记 -- 基础数据结构
redis笔记
基础的数据结构:string、list、hash、set、zset
容器型数据结构(list、hash、set、zset)通用规则
如果容器不存在,就创建一个,再进行操作如果容器里没有数据了,就立即删除,回收内存…
持续集成交付CICD:GitLabCI 运行前后端项目
目录
一、理论
1.spring项目自动构建
2.阿里云云效 Maven
3.Maven安装
4.Go安装
5.NPM安装
二、实验
1.GitLabCI 运行Maven项目
2.GitLabCI 运行Go项目
3.GitLabCI 运行NPM项目
三、问题
1.前端脚手架如何初始化项目
2.NPM下载如何指定
3.Go项目下载源如何指定 …
大数据-之LibrA数据库系统告警处理(ALM-37017 数据库连接数超限)
告警解释
当集群中单个CN实例上某个数据库的连接数超过限制时,产生该告警。
告警属性 告警ID 告警级别 可自动清除 37017 严重 是
告警参数 参数名称 参数含义 ServiceName 产生告警的服务名称 RoleName 产生告警的角色名称 HostName 产生告警的主机…
Vue生命周期:组件的生命之旅
🍃引言
在Vue.js中,每个组件都有其独特的生命周期。这个生命周期指的是组件从创建到销毁的一系列过程。了解并正确使用Vue的生命周期钩子,对于优化组件性能、管理组件状态以及实现特定功能至关重要。本文将详细介绍Vue的生命周期及其各个阶段…



:方差分析和参数估计)



)

 HelloWord)








)
