定义 :
并查集 : 一种数据结构,用于处理一些不相交集合的合并与查询问题;
例题 :
如 : 有n种元素,分属于不同的n个集合;
有两种操作 :
1.给出两个元素的亲属关系,合并两个集合(x与y是亲戚,亲戚的亲戚是亲戚);
于是[x所在的集合] 与 [y所在的集合] 合并;
2. 查询两个元素是否存在关系(是否再统一个集合之中)
实现 :
那么如何用数据结构来实现并查集呢?
一个集合构建一棵树,人选一个元素作为该集合的根节点,建立pre数组记录每个元素的父节点,pre[当前结点] = 父节点,根节点的父节点 = 自身本身 ;
将并查集,那么肯定有并 和 查 两个部分 :
并 :
那么给出元素关系之后,如何合并两个集合呢?
将一个集合的树编程另一个集合的字数(将一个集合的根节点的父节点 改为 另一个集合的根节点),用代码来表示也就是 : pre[B的根节点] = A 的根节点 , 就可以将两棵树合并为一棵树 (也就是森林转树);
查
如何查询两个元素是否属于同一个集合呢?
从该元素开始访问父节点(一般递归查找),知道一步步访问到根界点,再对两个元素的根节点进行对比判断(相同就属于同一集合 , 不相同就不属于同一个元素);
查找根节点的模板 :
int find(int x){if (pa[x] != x)pa[x] = find(pa[x]);return pa[x];}优化(路径压缩):
当上面并查集遇到这样的树的时候,时间优化就基本上没有了;
那么该如何避免这种情况呢?
这个时候就要用到路径压缩优化算法;
能发现 : 再查询操作时,最终目的 : 找到这个元素所在的这棵树的根结点,那么它和其它元素是如何联系的,对我们来说就没有任何意义了;
所以我们可以在每次查询结点的时候,对被查询结点到父节点沿途经过的结点进行一步路径压缩,将经过结点的父节点都更改为根节点 , 也就是 pre[经过结点] = 根节点;
让树的形状尽量接近下面 :

算法模板 :
基本模板
template <class T> struct DDS
{int pa[N], num[N];int size;void init(int x){size = x;for (int i = 1; i <= size; ++i)pa[i] = i;}int find(int x){if (pa[x] != x)pa[x] = find(pa[x]);return pa[x];}
};路径和模板
template <class T> struct DDS
{int pa[N], num[N];int size;void init(int x){size = x;for (int i = 1; i <= size; ++i)pa[i] = i;}int find(int x){if (pa[x] == x || pa[pa[x]] == pa[x])return pa[x];int p = find(pa[x]);num[x] += num[pa[x]];pa[x] = p;return p;}
};例题 : (NOI 2001 食物链)
链接 : 活动 - AcWing
带权并查集
两个元素建立联系时,并不只是将他们所在的集合合并,还要给它们之间赋一个权值,来表示它们之间的关系;
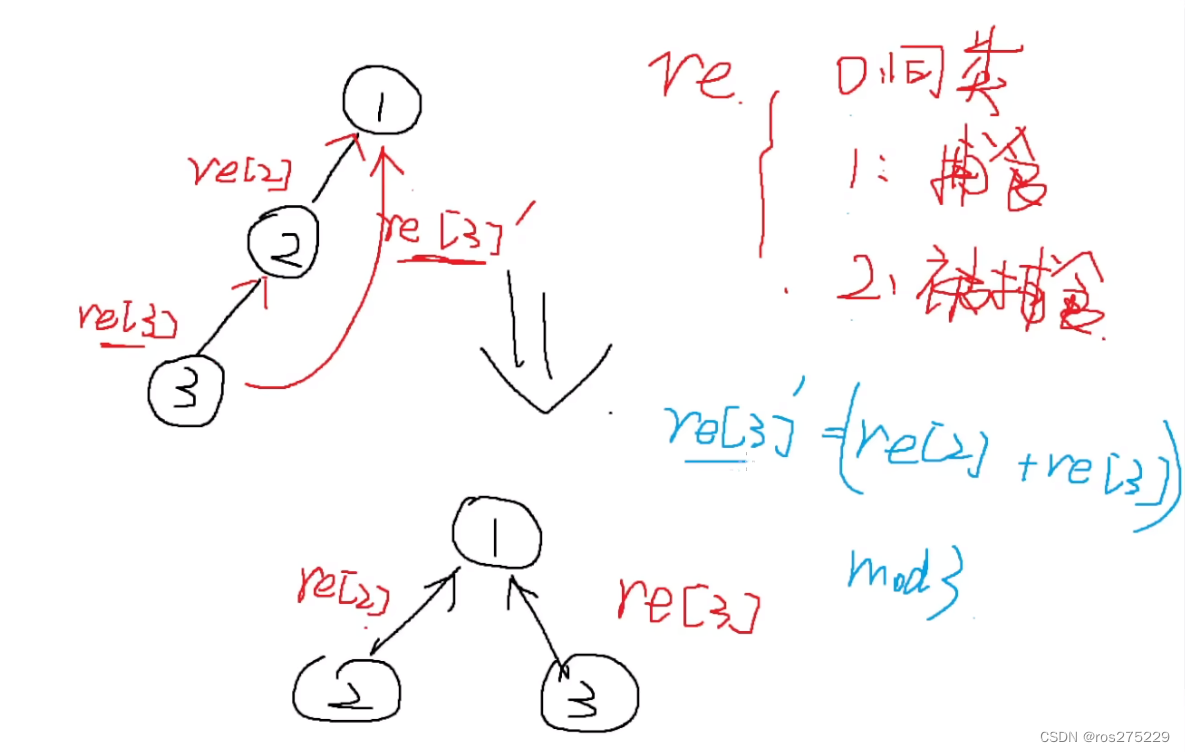
路径压缩时,3与1的关系要改为re[3]+re[2],但是只有0,1,2三种关系,所以还要对3取模;
在集合合并的时候,根节点之间的关系该如何赋值呢?
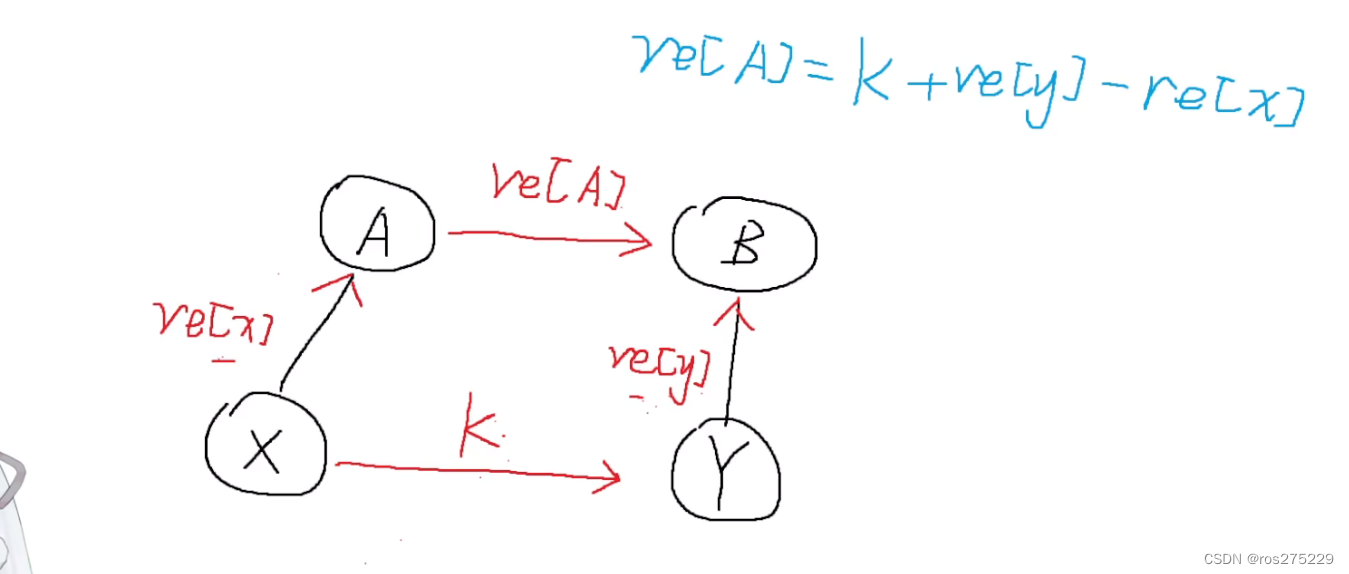
已知 x 对 y 的关系 : k, 还知道x对A的关系值 : re[x], Y对B的关系值 : re[y],用向量的思维,那么A对B的关系就是 : re[A] = k+re[y] - re[x] , 但是 re[y] - re[x] 是可能为负值的,所以改为 : re[A] = (k+re[y]-re[x] + 3) mod 3 ;
模板 :
int parent[N];
LL score[N];int find(int x){ // 找祖宗结点 if(x != parent[x]){int t = parent[x]; // 父节点 parent[x] = find(parent[x]); // 路径压缩score[x] += score[t]; // 加权合并 } return parent[x];
}