仅作自己学习使用
一、问题
旅行商问题(TSP) 是要求从一个城市出发,依次访问研究区所有的城市,并且只访问一次不能走回头路,最后回到起点,求一个使得总的周游路径最短的城市访问顺序。
采用模拟退火算法求解TSP问题,很自然的想到退火的目标函数(优化函数)应该就是总的周游距离。那么在算法中如何体现呢?那就是把城市的坐标放在一个n×2的矩阵中,矩阵中存放城市的顺序就是依次周游城市的路径,所以在求解过程中会不断的产生新的更优解(周游顺序,在算法中体现就是城市坐标的存放顺序),有了这个关键的思路就很好解决了。
二、Matlab代码
clear
clc
T1 = cputime;
C = [% 各个城市坐标39.91, 116.39; % 北京31.22, 121.48; % 上海23.13, 113.27; % 广州22.54, 114.06; % 深圳30.67, 104.06; % 成都34.27, 108.93; % 西安31.98, 118.75; % 南京39.92, 116.36; % 天津28.71, 115.83; % 南昌45.75, 126.63; % 哈尔滨36.07, 120.38; % 青岛38.04, 114.48; % 石家庄29.59, 106.54; % 重庆26.08, 119.30; % 福州30.25, 120.16; % 杭州28.19, 112.97; % 长沙25.03, 102.73; % 昆明35.68, 139.76; % 东京37.56, 126.97; % 首尔1.35, 103.82; % 新加坡13.41, 103.86; % 金边21.03, 105.85; % 河内3.14, 101.69; % 吉隆坡39.90, 32.85; % 安卡拉37.97, 23.73; % 雅典38.71, -9.14; % 里斯本41.89, 12.50; % 罗马52.52, 13.41; % 柏林55.75, 37.62; % 莫斯科48.86, 2.35; % 巴黎
];n = length(C); % 获取城市的个数
T = 100 * n; % 初始温度
L = 10; % 马尔可夫链长度
K = 0.986; % 降温系数%% 构建城市坐标结构体
city = struct([]);
for i = 1:ncity(i).x = C(i,1); % 经度city(i).y = C(i,2); % 纬度
end%% 开始退火
% 统计迭代次数
count = 1;
% 计算每次迭代后的总距离(第一次就是初始时,按照坐标的顺序计算的距离)
Dist(count) = GetDist(city,n);
figure(1)
% 当温度无限趋于0度时停止迭代
while T > 0.01 % 每次降温 均进行多次迭代for i = 1:L% 计算原路线周游距离len1 = GetDist(city,n);% 产生随机扰动(随机交换两个城市的坐标)p1 = floor(1 + n * rand()); % rand函数产生一个0,1之间均匀分布的实数,包含0但不包含1p2 = floor(1 + n * rand()); % 因此这个表达式可以产生一个从1到n的随机数while (p1 == p2)p1 = floor(1 + n * rand()); p2 = floor(1 + n * rand());endtemp_city = city;% 交换第P1个城市和第P2个城市的坐标temp = temp_city(p1);temp_city(p1) = temp_city(p2);temp_city(p2) = temp;% 计算新路线的周游距离len2 = GetDist(temp_city,n);% 新、老路线的差值(相当于能量)delta = len2 - len1;if(delta<0)% 新路线的评估函数更小(记住,模拟退火算法相当于是一个求函数极小值的算法)city = temp_city; % 更新原路线(变量里存放城市的顺序也就是访问城市的顺序)else% Metropolis接受准则(概率选择更差的解)if exp((len1-len2)/T) > rand()% 记住这个概率的公式,指数部分一定是要个负数,概率的值不可能超过1city = temp_city;endendend% 本次迭代结束,统计迭代次数加1count = count + 1; % 将本次迭代的最优解放在len中Dist(count) = GetDist(city,n); %% 本次退火结束,降温T = T * K;% 按照新的城市的顺序,把这些城市画出来for i = 1: n-1plot([city(i).x,city(i+1).x],[city(i).y,city(i+1).y],'bo-');hold on;endplot([city(n).x,city(1).x],[city(n).y,city(1).y],'ro-');title(['优化最短距离:', num2str(Dist(count))]);hold offpause(0.005); % 动态显示出每次的搜索结果
end
T2 = cputime;
figure(2)
plot(Dist,LineWidth=2)
xlabel("迭代次数")
ylabel("目标函数值")
title("适应度进化曲线","搜索时间:"+(T2-T1)+" s")
%% 评估函数
function result = GetDist(city,n)
% 计算总的周游路径长度(评估函数)
% city是各个城市的坐标result = 0;for i = 1:n-1result = result + sqrt((city(i).x - city(i+1).x)^2 + (city(i).y - city(i+1).y)^2);endresult = result + sqrt((city(n).x - city(1).x)^2 + (city(n).y - city(1).y)^2);
end
三、效果
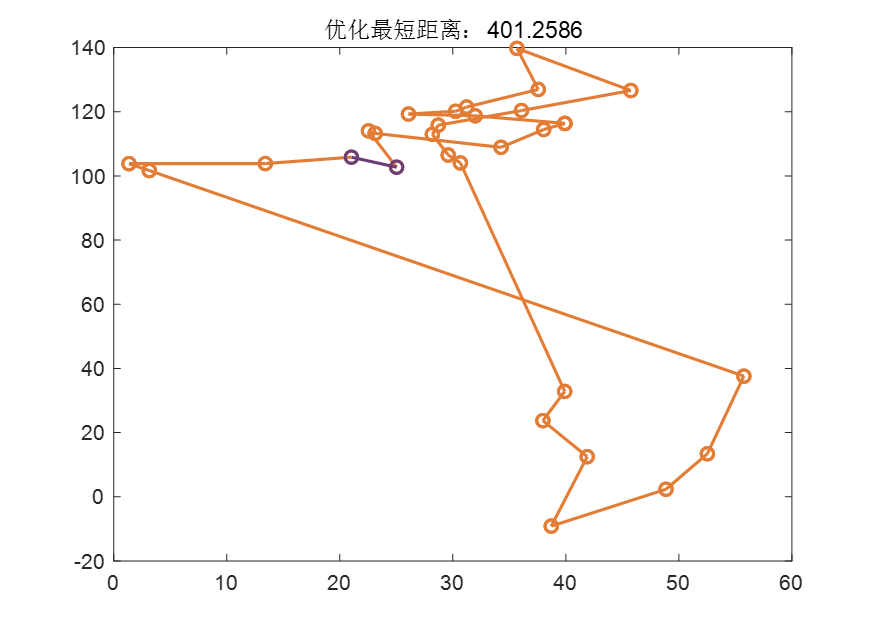
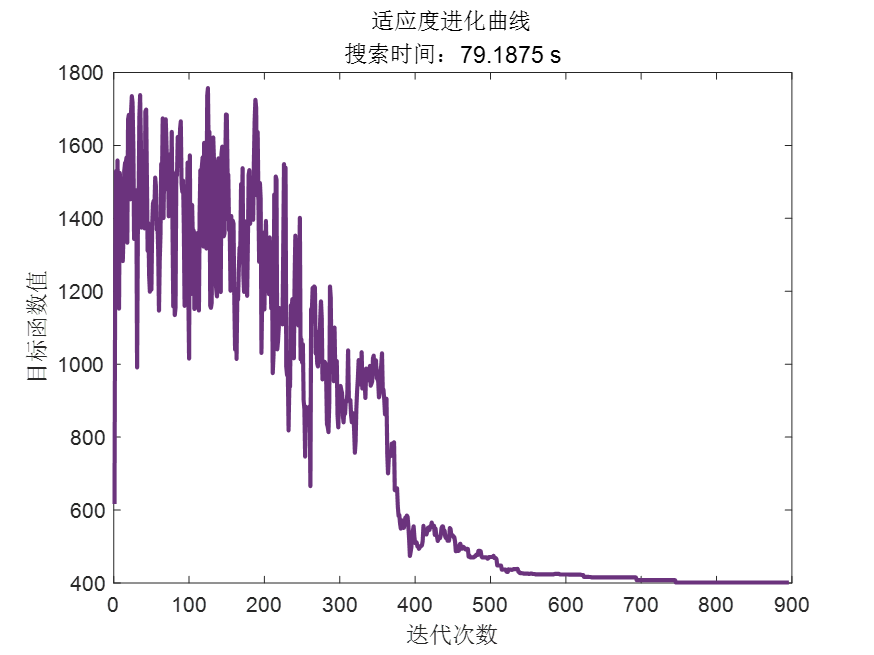
四、问题
大家可以试一试更多的城市,当有很多城市的坐标相差不大时,在最后的搜索结果中,会出现一个非常奇怪的问题,就是在周游图中,有些城市消失了,检查存放城市的city结构体,是存放着这些坐标的,这里如果有知道的朋友还请多多批评指教,我将及时改正。


)







)


:视频帧处理并用SDL渲染播放)

:从数据中发现洞察力)



