目录
有以下二叉树:
一、递归
1.1 前序遍历-递归
1.2 中序遍历-递归
1.3 后序遍历-递归
二、递归--使用链表
2.1 前序遍历-递归-返回链表
2.2 中序遍历-递归-返回链表
2.3 后序遍历-递归-返回链表
三、迭代--使用栈
3.1 前序遍历-迭代-使用栈
3.2 中序遍历-迭代-使用栈
3.3 后序遍历-迭代-使用栈
四、层序遍历
4.1 层序遍历-迭代-使用队列
4.2 层序遍历-迭代-返回二维链表
有以下二叉树:
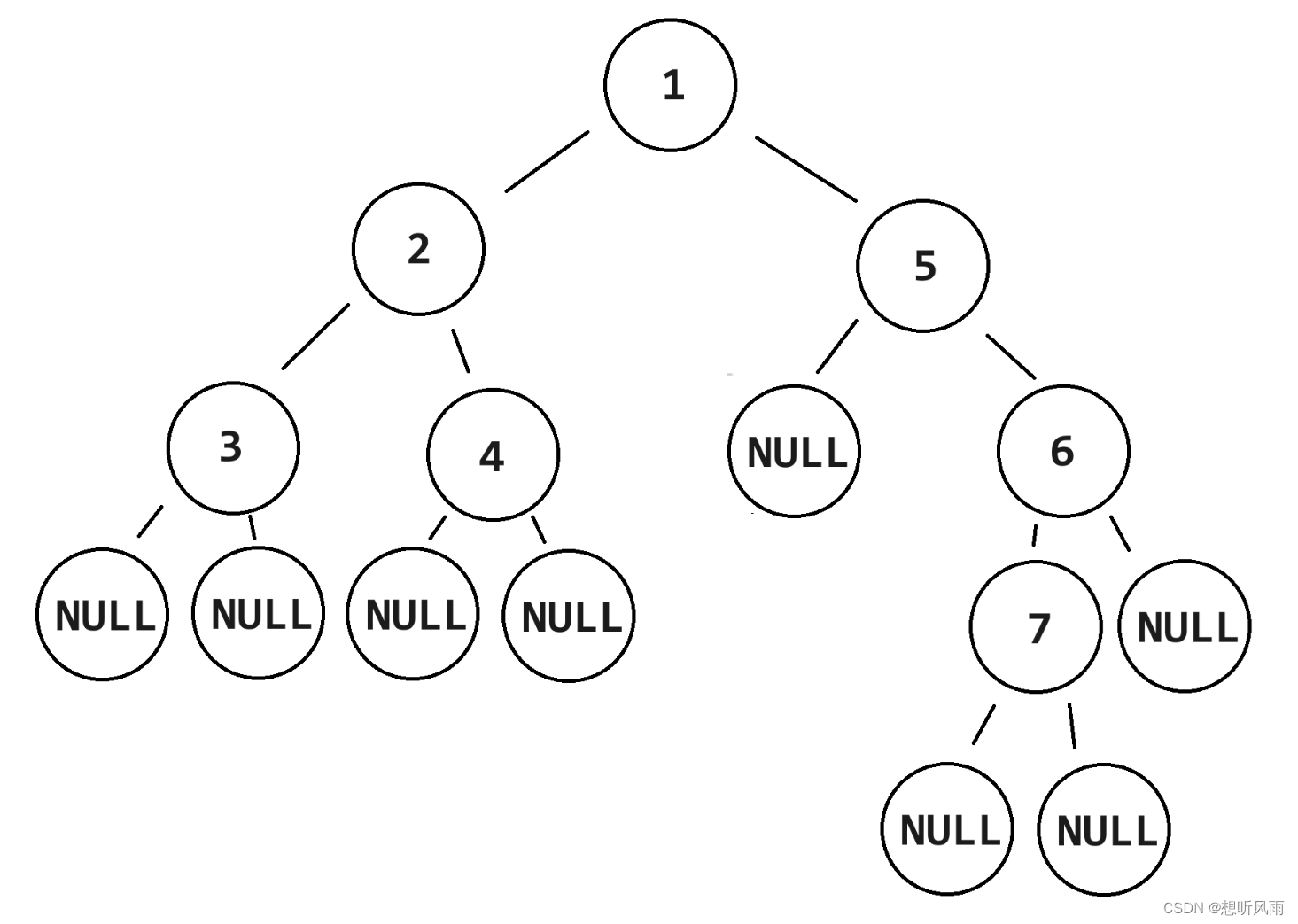
一、递归
| 逻辑/思路: | |
| 递归思想是将大问题分解为解法相似的小问题。 | |
| 已知根节点有左右子树,根节点的子节点又各有自己的左右子树,不断地对每棵子树进行左右分解,这就是从大问题到小问题。 | |
| 递归有两大关键条件:递推条件和回归条件,前者作用于递,后者作用于归。 | |
| 递推条件 | 在方法中,不断将左右子节点分别作为参数,重复调用本方法,每轮调用方法都在访问更深地子节点,达成了递归中的推进条件; |
| 回归条件 | 当访问到的节点为null时(如上图),就不能继续往下访问了,所以节点为null时,就return,这是回归条件; |
| 二叉树的前中后序递归遍历,思路基本相同,区别只在于调用方法和打印的顺序不同。 |
| 以下分别是二叉树的前序、中序、后序递归遍历的代码: |
1.1 前序遍历-递归
public static void PreorderTraversal1(TreeNode root) { //当前节点为null,则return;if(root == null){return;}//打印当前节点;System.out.print(root.val+" ");//找左子节点;PreorderTraversal1(root.left);//找右子节点;PreorderTraversal1(root.right);}//运行结果:
1 2 3 4 5 6 7 1.2 中序遍历-递归
public static void InorderTraversal1(TreeNode root) {//当前节点为null,则return;if(root == null){return;}//找左子节点;InorderTraversal1(root.left);//打印当前节点;System.out.print(root.val+" ");//找右子节点;InorderTraversal1(root.right);}//运行结果:
3 2 4 1 5 7 6 1.3 后序遍历-递归
public static void PostorderTraversal1(TreeNode root) {//当前节点为null,则return;if(root == null){return;}//找左子节点;PostorderTraversal1(root.left);//找右子节点;PostorderTraversal1(root.right);//打印当前节点;System.out.print(root.val+" ");}//运行结果:
3 4 2 7 6 5 1 二、递归--使用链表
| 逻辑/思路: | |
| 同样是使用递归的逻辑思想,只是由于使用了链表的数据结构,所以在递归的过程中需要将元素加入到链表中。 |
2.1 前序遍历-递归-返回链表
public static List<Integer> preorderTraversal2(TreeNode root){//新建链表;List<Integer> list = new ArrayList<>();//当前节点为null,则return;if(root == null){return list;}//add当前节点;list.add(root.val);//找当前节点的左子节点,并存储在新链表中;List<Integer> listLeft = preorderTraversal2(root.left);//将代表左子树的新链表中的元素全部添加到list中;list.addAll(listLeft);//找当前节点的右子节点,并存储在新链表中;List<Integer> listRight = preorderTraversal2(root.right);//将代表右子树的新链表中的元素全部添加到list中;list.addAll(listRight);//返回代表这个子树的list;return list;}//运行结果:
1 2 3 4 5 6 7 2.2 中序遍历-递归-返回链表
public static List<Integer> InorderTraversal2(TreeNode root){//新建链表;List<Integer> list = new ArrayList<>();//当前节点为null,则return;if(root == null){return list;}//找当前节点的左子节点,并存储在新链表中;List<Integer> listLeft = InorderTraversal2(root.left);//将代表左子树的新链表中的元素全部添加到list中;list.addAll(listLeft);//add当前节点;list.add(root.val);//找当前节点的右子节点,并存储在新链表中;List<Integer> listRight = InorderTraversal2(root.right);//将代表右子树的新链表中的元素全部添加到list中;list.addAll(listRight);//返回代表这个子树的list;return list;}//运行结果:
3 2 4 1 5 7 6 2.3 后序遍历-递归-返回链表
public static List<Integer> PostorderTraversal2(TreeNode root){//新建链表;List<Integer> list = new ArrayList<>();//当前节点为null,则return;if(root == null){return list;}//找当前节点的左子节点,并存储在新链表中;List<Integer> listLeft = PostorderTraversal2(root.left);//将代表左子树的新链表中的元素全部添加到list中;list.addAll(listLeft);//找当前节点的右子节点,并存储在新链表中;List<Integer> listRight = PostorderTraversal2(root.right);//将代表右子树的新链表中的元素全部添加到list中;list.addAll(listRight);//add当前节点;list.add(root.val);//返回代表这个子树的list;return list;}//运行结果:
3 4 2 7 6 5 1 三、迭代--使用栈
| 逻辑/思路: | |
| 迭代是使用栈来帮助遍历二叉树。这种遍历方式利用了栈“后进先出”的特点,来达到对二叉树中的父节点进行回溯的目的。 也就是说,当遍历到一个节点即将该节点压栈,当完成对左子树的访问之后,利用弹出并记录栈顶元素的方式,得到左子树的父节点,并通过这个父节点访问右子树。 因为压栈的第一个元素必然为根节点,因此,当栈为空时,必然全部节点都遍历完成了。 |
3.1 前序遍历-迭代-使用栈
public static void PreorderTraversal3(TreeNode root){//如果root为null,return;if(root == null){return;}//新建一个栈;Stack<TreeNode> stack = new Stack<>();//将根节点压栈;stack.push(root);//如果栈不为空;while (!stack.isEmpty()){//弹出栈顶元素,并记录为cur;TreeNode cur = stack.pop();//因为是前序遍历,打印当前节点,再进行后续操作;System.out.print(cur.val+" ");//如果cur的右子节点不为空,则将其压栈;if(cur.right != null){stack.push(cur.right);}//如果cur的左子节点不为空,则将其压栈;if(cur.left != null){stack.push(cur.left);}}}//运行结果:
1 2 3 4 5 6 7 | 为什么压栈先压右子节点,再压左子节点? |
| 因为要按前序遍历打印,而栈是后进先出,所以后压左子节点,等下先弹出的也是左子节点,先弹出先打印。 |
3.2 中序遍历-迭代-使用栈
public static void InorderTraversal3(TreeNode root){//如果root为null,return;if(root == null){return;}//新建一个栈;Stack<TreeNode> stack = new Stack<>();//用一个临时“指针”记录root(因为要移动指针,不然等下根节点跑哪去都不知道了)TreeNode cur = root;//如果cur不为空或者栈不为空;while (cur != null || !stack.isEmpty()){//如果节点不为空,则将节点压栈,并让指针不断向左子节点移动,直到节点为空;//当循环停下时,此时栈顶元素必然是树中最左边且未被遍历过的节点;while (cur != null){stack.push(cur);cur = cur.left;}//弹出栈顶元素,并记录为pre;TreeNode pre = stack.pop();//因为是中序遍历,打印当前节点,再进行后续操作;System.out.print(pre.val+" ");//如果pre的右子节点不为空,则将指针cur移动到右子节点上;if(pre.right != null){cur = pre.right;}}}//运行结果:
3 2 4 1 5 7 6 | 为什么进入循环的判断条件是cur != null || !stack.isEmpty()? |
| cur不为空的判断条件是为了让一开始栈中还没有元素时,能够顺利进入循环。 栈不为空代表还有元素没有遍历。 |
3.3 后序遍历-迭代-使用栈
public static void PostorderTraversal3(TreeNode root){//如果root为null,return;if(root == null){return;}//新建一个栈;Stack<TreeNode> stack = new Stack<>();//用一个临时“指针”记录root(因为要移动指针,不然等下根节点跑哪去都不知道了)TreeNode cur = root;//将根节点压栈;stack.push(root);//如果栈不为空;while (!stack.isEmpty()) {//查看并记录栈顶元素这个节点;TreeNode peek = stack.peek();//根据以下条件,进行后续操作;if (peek.left != null && peek.left != cur && peek.right != cur) {stack.push(peek.left);} else if (peek.right != null && peek.right != cur) {stack.push(peek.right);} else {System.out.print(stack.pop().val + " ");cur = peek;}}}//运行结果:
3 4 2 7 6 5 1 | 上述代码中的 if...else if..else 为什么这样设置条件? | |
| if (peek.left != null && peek.left != cur && peek.right != cur) { stack.push(peek.left); } | |
| 判断peek有没有左子节点,且peek的左右子节点有没有被处理过; | |
| 如果左右子节点都没有被处理过,那么将peek的左子节点压栈; | |
| else if (peek.right != null && peek.right != cur) { stack.push(peek.right); } | |
| 再判断peek有没有右子节点,且peek的右子节点有没有被处理过; | |
| 在这里不能对左子节点判断是否操作过,因为是先遍历的左子节点,如果存在左子节点必然是操作过的。所以如果加入左子节点的判断,则必然进不了这个else if; | |
| 如果右子节点没有被处理过,那么将peek的右子节点压栈; | |
| 通过前两个条件可以看出,只要有左子节点,必然先处理左子节点,没有左子节点或者左子节点被处理完了,才开始处理右子节点;处理方法如下: | |
| else { System.out.print(stack.pop().val + " "); cur = peek; } | |
| 直到所有左右子节点处理完毕,最后一个弹出栈并被处理的,必然是一开始压栈的根节点root。 | |
四、层序遍历
| 逻辑/思路: | |
| 层序遍历与前序、中序、后序遍历都不同,层序遍历使用的是队列的数据结构进行遍历。 核心思想是利用队列“先进先出”和“队头出,队尾入”的特点,分层遍历二叉树。 如果需要返回一个二维链表,则是将二叉树每层的节点按顺序添加到各个链表中,每个链表代表一层,最终链表将作为元素,被添加到二维链表中; |
4.1 层序遍历-迭代-使用队列
public static void SequenceTraversal1(TreeNode root){//如果root为null,return;if(root == null){return;}//创建队列,root入队列;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);//如果队列中还有元素;while (queue.size() != 0){//队首出队列并记录cur;TreeNode cur = queue.poll();//打印cur的值;System.out.print(cur.val + " ");//如果cur有左子节点,将左子节点入队列;if(cur.left != null){queue.offer(cur.left);}//如果cur有右子节点,将右子节点入队列;if(cur.right != null){queue.offer(cur.right);}}}//运行结果:
1 2 5 3 4 6 7 4.2 层序遍历-迭代-返回二维链表
public static List<List<Integer>> SequenceTraversal2(TreeNode root){//创建二维链表diList;List<List<Integer>> diList = new LinkedList<>();//如果root为空则return;if(root == null){return diList;}//创建队列,root入队列;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);//如果队列中还有元素;while(!queue.isEmpty()){//计算队列中的元素数量;int size = queue.size();//创建链表,用于存储每层的节点;List<Integer> list = new LinkedList<>();//根据上面的size确定需要循环多少次,即处理多少个节点;while (size>0){//队首出队列;TreeNode cur = queue.poll();//出队列一个size就--;size--;//把出队列的元素添加到list中;list.add(cur.val);//如果cur有左子节点,将左子节点入队列;if(cur.left != null){queue.offer(cur.left);}//如果cur有右子节点,将右子节点入队列;if(cur.right != null){queue.offer(cur.right);}}//把链表list添加到diList中;diList.add(list);}//返回diList;return diList;}//运行结果:
1 2 5 3 4 6 7 
)


--练习题)

 一行炸裂指定行)
:好子数组的最大分数)











