Dijkstra算法（贪心），Floyd-Warshall算法（动态规划）， Bellman-Ford算法——用Python实现

图论中最短路径三剑客

  • 前言
  • 一、Dijkstra算法（贪心）
    • 1.1 Dijkstra在生活中的应用举例
    • 1.2 设计思路
    • 1.3 算法应用实例
      • 1.3.1 以交通规划为例
      • 1.3.2 Dijkstra算法执行步骤
      • 1.3.3 python代码
    • 1.4 时空复杂度
  • 二、Floyd-Warshall算法（动态规划）
    • 2.1 Floyd-Warshall在生活中的应用举例
    • 2.2 设计思路
    • 2.3 算法应用实例
      • 2.3.1 以交通路线为例(用原理)
      • 2.3.2 Floyd-Warshall算法执行步骤（原理）
        • 2.3.3 python代码
      • 2.3.4 Floyd-Warshall算法执行步骤（用矩阵来直接计算）
    • 2.4 时空复杂度
  • 三、Bellman-Ford算法
    • 3.1 Bellman-Ford算法在生活中的应用举例
    • 3.2 Bellman-Ford算法的核心思想
    • 3.3 算法应用实例
      • 3.3.1 Bellman-Ford算法在金融决策方面的应用
      • 3.3.2 Python代码
      • 3.4 时空复杂度
  • 总结：三者比较

前言

  图算法在解决网络和路径问题中发挥着关键作用，而Dijkstra算法、Floyd-Warshall算法和Bellman-Ford算法是图算法家族中的重要成员。

Dijkstra算法（贪心）

  解决非负权边（也就是只能为正边）图中最短路径问题的贪心算法，通过逐步选择当前最短路径的节点，求解从给定起始节点到其他所有节点的最短路径（找到单源最短路径的贪心算法）。

  简而言之，从一个节点到所有其他节点的最短路径。

Floyd-Warshall算法（动态规划）

  解决有向图中所有节点对最短路径问题的动态规划算法，通过逐步优化节点对之间的最短路径，适用于权值为正或负的有向图（全源最短路径）。

  简而言之，所有顶点间的最短路径，允许负权边。

Bellman-Ford算法

  解决带有负权边图中最短路径问题的动态规划算法，通过对所有边进行松弛操作，逐步优化从源节点到其他所有节点的最短路径。特别擅长检测负权回路。

  简而言之，Bellman-Ford算法可以求带负权边的图的单源最短路，并且可以判断图是否存在负环。存在负环的图求最短路是没有意义的因为它的路径权会无限缩小

一、Dijkstra算法（贪心）

1.1 Dijkstra在生活中的应用举例

网络路由： 在计算机网络中，Dijkstra算法可以用于找到数据包从源节点到目标节点的最短路径，确保网络通信的效率和快速传输。

交通规划： 在城市交通规划中，Dijkstra算法可以用于寻找最短路径，帮助驾驶导航系统计算最快到达目的地的路线。

航空业： 航空公司可以使用Dijkstra算法来规划最短的航班路径，以减少燃料消耗和飞行时间。

电信网络： 运营商可以利用Dijkstra算法来规划光纤或电信线路的布局，确保信息传输的最短路径。

物流和配送： 在物流行业，Dijkstra算法可用于规划货物运输的最短路径，降低运输成本和时间。

1.2 设计思路

  Dijkstra算法是一种贪心算法，通过选择当前最短路径的节点，并更新其邻居的路径长度，逐步确定起始节点到其他节点的最短路径。

  即每次选择当前最短路径，逐步构建最短路径集合。通过不断更新节点的距离来逼近最短路径。

1.3 算法应用实例

1.3.1 以交通规划为例

  以交通规划为例子，有ABCDEF6个地方，权重表示距离（公里），我们想要从城市 A 出发，找到最短路径到达城市 F。我们可以使用Dijkstra算法进行计算。
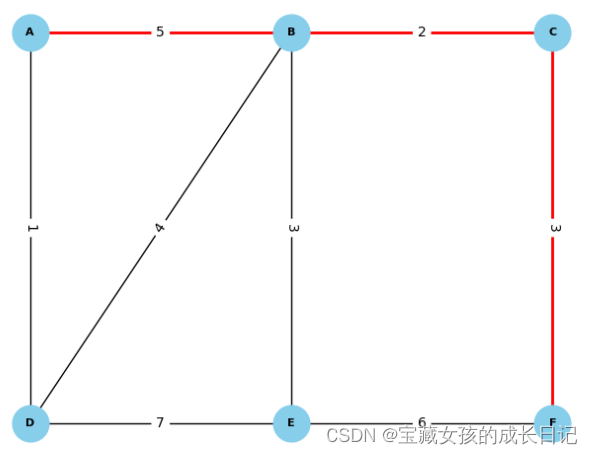
在这里插入图片描述

1.3.2 Dijkstra算法执行步骤

  1. 初始化A到各个城市的距离为无穷大(∞)，A到自身的距离为0。
  2. 从A开始，遍历所有相邻城市，更新A到这些城市的距离。
  3. 选择距离最短的城市作为当前城市，标记为已访问。
  4. 针对当前城市的相邻城市，更新A到这些城市的距离，如果有更短的路径。

重复步骤3和步骤4，直到所有城市都被访问过。

手写的A分别到BCDEF的最短路径结果

在这里插入图片描述

1.3.3 python代码

import networkx as nx
import matplotlib.pyplot as plt# 创建图
G = nx.Graph()# 添加节点和边
edges = [('A', 'B', {'weight': 5}),('A', 'D', {'weight': 1}),('B', 'C', {'weight': 2}),('B', 'D', {'weight': 4}),('B', 'E', {'weight': 3}),('C', 'F', {'weight': 3}),('D', 'E', {'weight': 7}),('E', 'F', {'weight': 6})]G.add_edges_from(edges)# 计算最短路径
shortest_path = nx.shortest_path(G, source='A', target='F', weight='weight')
print("Shortest Path:", shortest_path)
shortest_distance = nx.shortest_path_length(G, source='A', target='F', weight='weight')
print("Shortest Distance:", shortest_distance)# 绘制图形
pos = {'A': (0, 0), 'B': (1, 0), 'C': (2, 0), 'D': (0, -1), 'E': (1, -1), 'F': (2, -1)}
nx.draw(G, pos, with_labels=True, font_weight='bold', node_size=700, node_color='skyblue', font_color='black', font_size=8)# 绘制最短路径
edges_in_shortest_path = [(shortest_path[i], shortest_path[i + 1]) for i in range(len(shortest_path) - 1)]
nx.draw_networkx_edges(G, pos, edgelist=edges_in_shortest_path, edge_color='red', width=2)# 添加边的权重标签
edge_labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)# 显示图形
plt.show()

得到的结果就是1.3.1的图。

1.4 时空复杂度

  1. 时间复杂度
    Dijkstra算法的时间复杂度取决于图的规模，通常为O(V^2)，其中V是节点的数量。
    然而，通过使用优先队列等数据结构，可以将时间复杂度优化到O((V + E) * log(V))，其中E是边的数量

  2. 空间复杂度： 在最坏情况下，空间复杂度为O(V)，其中V是顶点数。
    以1.3为例，在给定的例子中，有 6 个顶点（A、B、C、D、E、F）和 8 条边，所以 V = 6，E = 8。这样，时间复杂度可以表示为 O((6 + 8) * log(6))，空间复杂度为 O(6)。

注意：Dijkstra算法无法解决有负边的情况。

二、Floyd-Warshall算法（动态规划）

这儿有个视频讲得很好：https://www.youtube.com/watch?v=oNI0rf2P9gE

区别与找到单源最短路径的贪心算法（Dijkstra）， Floyd-Warshall是全源最短路径，并且可以出现负边。

2.1 Floyd-Warshall在生活中的应用举例

网络路由算法： 在计算机网络中，Floyd-Warshall算法可用于确定不同点的最短路径，以帮助路由数据包通过网络。

交通规划： 在城市交通规划中，Floyd-Warshall算法可以用于计算不同地点的最短路径，以优化交通流和减少拥堵。

航空业： 航班调度和路径规划中，Floyd-Warshall算法可以帮助确定不同城市之间的最短飞行路径。

电信网络规划： 在电信领域，Floyd-Warshall算法可以用于确定通信网络中不同节点之间的最短路径，以提高数据传输效率。

物流和运输： 在物流和运输领域，Floyd-Warshall算法可以用于计算多个货物从生产地到目的地的最短路径，以降低运输成本。

城市规划： 在城市规划中，Floyd-Warshall算法可以用于分析城市中不同地点之间的最短路径，以优化基础设施和服务的布局。

2.2 设计思路

Floyd-Warshall算法的设计思路是通过不断迭代更新路径信息，从而找到图中所有点对之间的最短路径。

算法的核心思想是逐步优化路径长度矩阵，直到找到所有点对之间的最短路径。这样，算法适用于解决所有点对之间的最短路径问题，而不需要针对每一对点单独计算。

2.3 算法应用实例

2.3.1 以交通路线为例(用原理)

A、B、C分别表示三个城市，边的权重表示从一个城市到另一个城市的路径长度。给定的邻接矩阵表示城市之间的路径长度，其中∞表示两城市之间没有直接路径。现在要找出每个城市到每个城市的最短距离。

有矩阵：

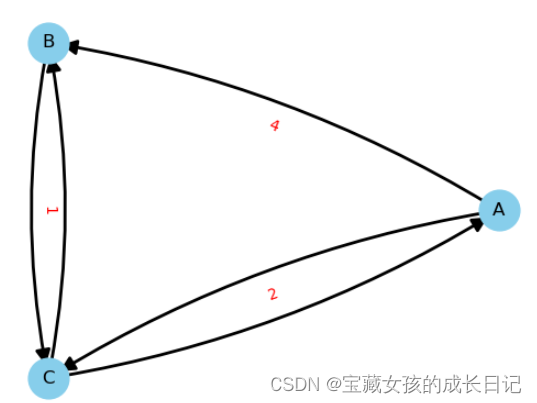
在这里插入图片描述
在这里插入图片描述

2.3.2 Floyd-Warshall算法执行步骤（原理）

构造一个距离矩阵

ABC
A042
B∞01
C210

初始的前驱矩阵（Predecessor Matrix）如下（-1表示无前驱节点）：

ABC
A-1-1-1
B-1-1-1
C-1-1-1

现在，我们开始使用Floyd-Warshall算法的迭代过程。

  1. 借助A间接到达其它顶点（分析：借助A，然后A到ABC本身没有意义，所以第一行保持不变；B没有到A的路径，所以B这一列仍然不变；再来看C，C借助A到A不还是C到A么？C借助A到B为2+4=6大于C直接到B的权值1，显然我们要求最短的路径，因此只要1，C借助A到C这就不用看了，对角始终为0，因为自己到自己始终是0。）
ABC
A042
B∞01
C210

  在这一轮中，没有找到更短的路径，所以Predecessor Matrix保持不变。

  1. 借助B间接到达其它顶点（分析：借助B，A借助B到B还是4，A借助B到C为4+1=5>A直接到C（2）因此不变；B到A没有路，因此仍然是无穷，B借助B到B自身肯定是0，自身没有意义，还是0，B借助B到C还是1；C借助B到A，由于B到A不通，所以是无穷。无穷大于2，因此2不变，C借助B到B还是1，C借助B到C自身还是0。）
ABC
A042
B∞01
C210

  在这一轮中，没有找到更短的路径，所以Predecessor Matrix保持不变。

  1. 借助C间接到达其它顶点（分析：借助C，A借助C到A还是0，A借助C到B为2+1=3>A直接到B（4）因此3替换4, A借助C到C还是2；B借助C到A为1+2=3小于B到A（无穷），因此3替换掉无穷，B借助C到B自身没有意义，还是0，B借助C到C还是1；借助C，然后C到ABC本身没有意义，不做比较。）
ABC
A032
B301
C210

最终，我们得到了最终的距离矩阵和前驱节点矩阵：
Final Distance Matrix:

ABC
A032
B301
C210

Predecessor Matrix:

ABC
A-12-1
B2-1-1
C-1-1-1
2.3.3 python代码
import numpy as np# 定义无穷大
INF = float('inf')# 定义图的邻接矩阵
graph = np.array([[0, 4, 2],[INF, 0, 1],[2, 1, 0]])# 获取节点个数
n = len(graph)# 初始化距离矩阵和前驱节点矩阵
distance_matrix = graph.copy()
predecessor_matrix = np.full((n, n), -1)# Floyd-Warshall算法
for k in range(n):for i in range(n):for j in range(n):if distance_matrix[i][j] > distance_matrix[i][k] + distance_matrix[k][j]:distance_matrix[i][j] = distance_matrix[i][k] + distance_matrix[k][j]predecessor_matrix[i][j] = k# 打印最终的距离矩阵和前驱节点矩阵
print("Final Distance Matrix:")
print(distance_matrix)
print("\nPredecessor Matrix:")
print(predecessor_matrix)

运行结果：
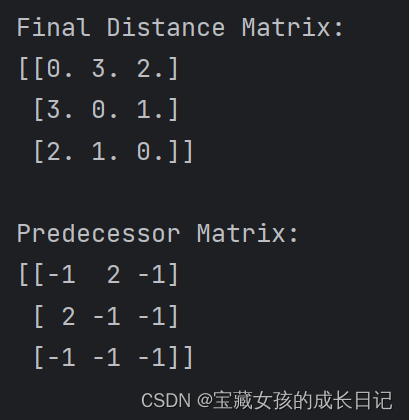
在这里插入图片描述

2.3.4 Floyd-Warshall算法执行步骤（用矩阵来直接计算）

注意：
i为行，j为列，先行后列。
自己到自己始终是0，没有任何路径比自己到自己还小的，因此正对角线没有意义直接不看。
首先标出第k行和第k列（k>=1），对角线不参与计算，留出空白与第一行和第一列相加比大小。

  1. 借助A间接到达其它顶点
    将第一列和第一行和对角线标上特殊的颜色，此时我们要计算特别的空白的值，是否有
    在这里插入图片描述
    直接来看例子：
    例如，d(21)+d(13)=无穷+2>d(23)，因此d(23)=1不动；如果d(21)+d(13)=无穷+2<d(23)，那么d(23)就要更新。
    以此类推…d(32)同理。
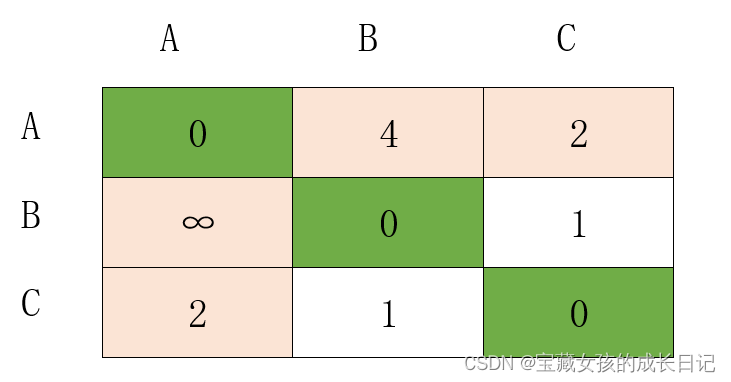
    在这里插入图片描述

  2. 借助B间接到达其它顶点
    同上。
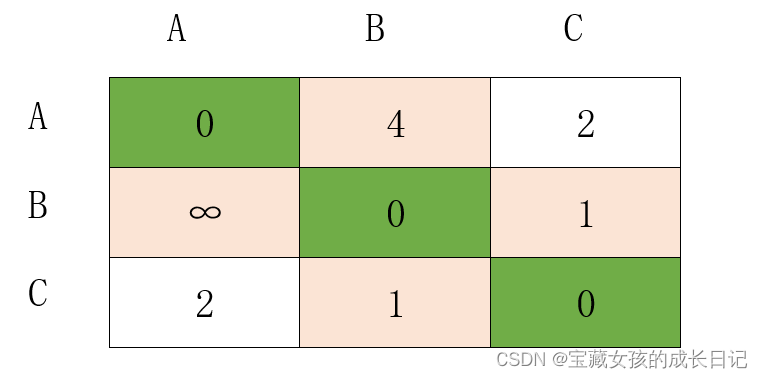
    在这里插入图片描述

  3. 借助C间接到达其它顶点
    这里可以看到，
    d(13)+d(32)=2+1=3 < d(12)=4
    d(23)+d(31)=2+1=3 < d(21)=∞
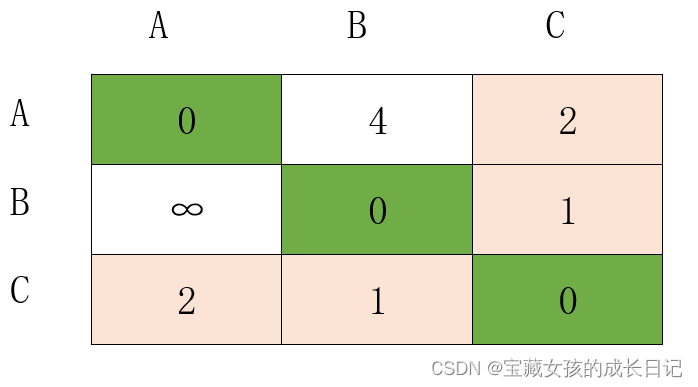
    在这里插入图片描述
    因此更新值。这是最终结果：
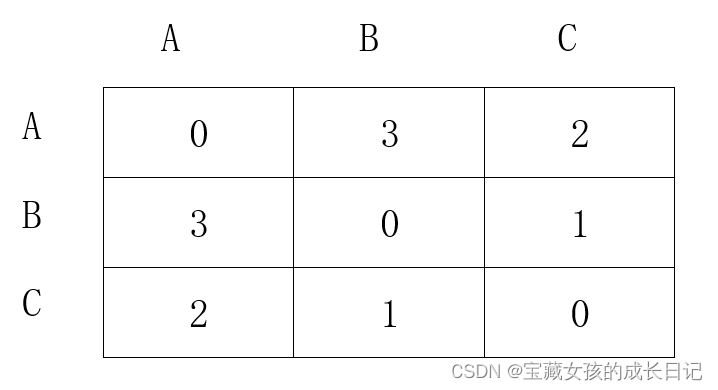
    在这里插入图片描述

2.4 时空复杂度

  1. 时间复杂度： O(V^3)
    V 是图中的顶点数。
    由于算法需要计算所有顶点对之间的最短路径，它的时间复杂度是三重循环的结果。

  2. 空间复杂度： O(V^2)
    Floyd-Warshall算法的空间复杂度为O(V^2)，这是因为算法需要存储每一对顶点之间的最短路径长度。对于每一对顶点(i, j)，我们只需使用O(1)的空间来存储它们之间的最短路径长度，但由于存在V × V对的顶点，所以总的空间复杂度为O(V^2)。

三、Bellman-Ford算法

参考youtube的视频：https://www.youtube.com/watch?v=FtN3BYH2Zes&t=10s
这是目前为止我觉得讲得最清楚的了。

3.1 Bellman-Ford算法在生活中的应用举例

  1. 负权边的存在

场景： 银行资金流动。
解释： 在金融系统中，资金流动可能涉及到费用或成本，而这些成本可能是负数。Bellman-Ford算法可以用于计算最短路径，考虑到负数成本，以便选择费用最小的路径。

  1. 动态图变化较小

场景： 网络路由变化较少。
解释： 在计算机网络中，路由信息可能会发生变化，但这些变化可能是相对较小的，例如一些路由器的状态发生变化。Bellman-Ford算法适用于这种情况，因为它能够在图变化较小的情况下快速适应。

  1. 图的规模较小

场景： 城市之间的交通网络。
解释： 考虑一个较小的城市交通网络，其中城市是节点，道路是边。由于规模较小，Bellman-Ford算法可能在计算城市之间最短路径时比Dijkstra算法更有效。

  1. 负权环的检测

场景： 金融交易的环路检测。
解释： 在金融交易中，如果存在环路，可能导致无限循环的负债。Bellman-Ford算法可以用于检测是否存在这样的负权环。

3.2 Bellman-Ford算法的核心思想

  如果一个图没有负权环，从一点到另外一点的最短路径，最多经过所有的V个顶线，有V-1条边,否则，存在顶点经过了两次，既存在负权环。

算法过程：
初始化： 首先，将源节点到所有其他节点的距离初始化为无穷大，将源节点的距离初始化为0。这个步骤确保了在算法开始时，只有源节点的距离是已知的，其他节点的距离是未知的。
（图来自Abdul Bari也就是上面那个视频）
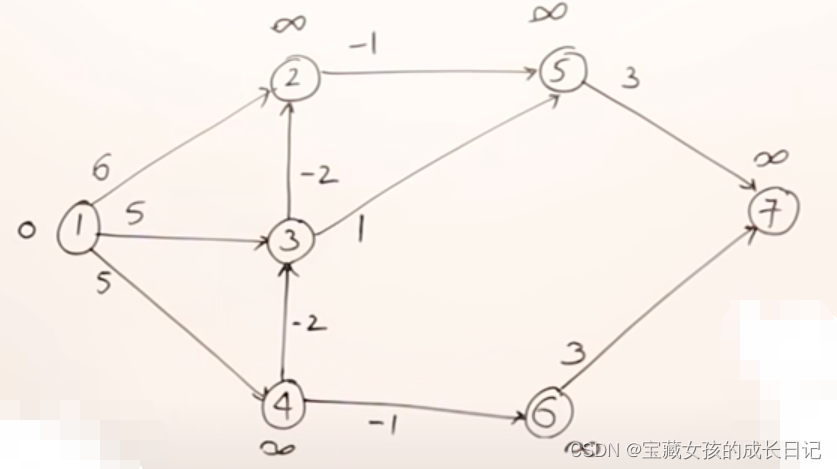
在这里插入图片描述

松弛操作： 算法通过多轮的松弛操作来逐步更新节点之间的最短路径。对于每一条边 (u, v)，尝试通过该边松弛节点 v 的距离。即，检查是否通过节点 u 可以找到一条到节点 v 更短的路径。

多轮迭代： Bellman-Ford算法采用多轮迭代的方式，每一轮都尝试通过所有边进行松弛操作。这是为了确保在最坏情况下，算法能够找到从源节点到所有其他节点的最短路径。通常需要进行 |V| - 1 轮迭代，其中 |V| 是节点的数量。

（图来自Abdul Bari）
在这里插入图片描述

检测负权环： 在进行 |V| - 1 轮迭代之后，算法会检查是否存在负权环。如果在第 |V| 次迭代中，仍然可以通过边松弛节点的距离，说明图中存在负权环。存在负权环意味着没有有限的最短路径，因为可以通过环路反复减小路径长度。

3.3 算法应用实例

3.3.1 Bellman-Ford算法在金融决策方面的应用

问题：
假设你是一位金融分析师，有一系列不同的金融资产，每个资产之间存在交易关系，而每个交易都有相关的成本。你希望找到从特定资产到其他所有资产的最短路径，考虑到每个交易的成本。使用Bellman-Ford算法解决这个实际金融问题。

具体表述如下：

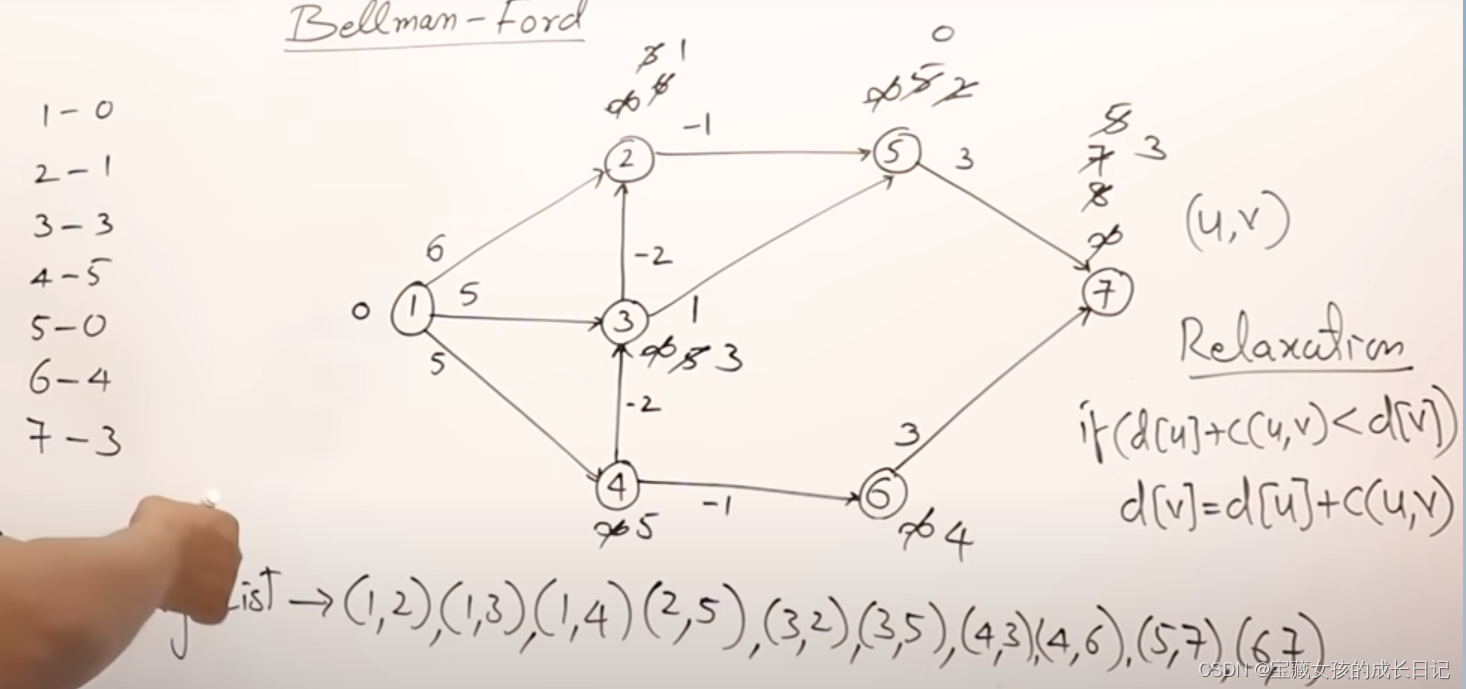
transactions = [(1, 2, 6),(1, 3, 5),(1, 4, 5),(2, 5, -1),(3, 2, -2),(4, 3, -2),(3, 5, 1),(4, 6, -1),(5, 7, 3),(6, 7, 3)
]

每个元组的三个值分别表示从一个资产到另一个资产的交易成本。Bellman-Ford算法用于找到从指定的起始资产到所有其他资产的最短路径，考虑到每个交易的成本。在这个特定的例子中，起始节点是资产 1。

3.3.2 Python代码

def bellman_ford(graph, start):# 初始化距离数组n = max(max(u, v) for u, v, _ in graph) + 1dist = [float('inf')] * ndist[start] = 0# 多轮迭代for _ in range(n - 1):# 对每条边进行松弛操作for u, v, weight in graph:if dist[u] + weight < dist[v]:dist[v] = dist[u] + weight# 输出每一轮迭代后的距离情况print(f"Iteration {_ + 1}: {dist}")# 检查是否存在负权环for u, v, weight in graph:if dist[u] + weight < dist[v]:print("图中存在负权环，无法找到最短路径")return Nonereturn dist# 示例图的边和权重表示
graph_example = [(1, 2, 6),(1, 3, 5),(1, 4, 5),(2, 5, -1),(3, 2, -2),(4, 3, -2),(3, 5, 1),(4, 6, -1),(5, 7, 3),(6, 7, 3)
]# 运行Bellman-Ford算法
start_node = 1
result = bellman_ford(graph_example, start_node)# 输出最终的最短路径结果
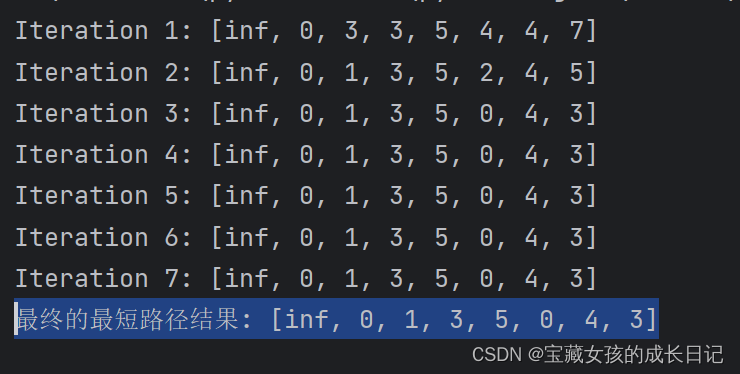
print("最终的最短路径结果:", result)

运行结果：

在这里插入图片描述

3.4 时空复杂度

  1. 时间复杂度
    Bellman-Ford算法的时间复杂度是O(V * E)，其中V是顶点数，E是边数。

  2. 空间复杂度
    空间复杂度是O(V)，主要用于存储距离数组和其他辅助数据结构。

总结：三者比较

Dijkstra算法（贪心）

优点：
针对单源最短路径问题的正权重图，Dijkstra算法的效率较高。
适用于图中边的权重为非负数的情况。
缺点：
无法处理带有负权重边的图，因为它基于贪心策略，每一步都选择当前最短路径，而负权重可能导致在后续的步骤中发现更短的路径。
对于稀疏图，使用优先队列实现的Dijkstra算法可能更有效。

Floyd-Warshall算法（动态规划）

优点：
适用于包含负权重边和带有负权重环的图。
能够计算任意两点之间的最短路径。
缺点：
时间和空间复杂度较高，不适用于大规模图。
不适合处理动态图的情况，因为每次都要重新计算所有顶点对之间的最短路径。

Bellman-Ford算法

优点：
能够处理带有负权重边的图，并能够检测负权重环的存在。
适用于单源最短路径问题。
缺点：
时间复杂度较高，为O(V * E)，其中V是顶点数，E是边数。
在一般情况下，对于正权重图，性能可能不如Dijkstra算法。
不如Floyd-Warshall算法适用于所有顶点对的最短路径问题。

使用范围：

使用Dijkstra算法时，图应该是无负权重的。
使用Floyd-Warshall算法时，可以处理带有负权重边和负权重环的图，但不适用于大规模图。
使用Bellman-Ford算法时，可以处理带有负权重边的图，并能够检测负权重环。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/179955.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

fiddler设置过滤你就这样做，一做一个不只声！

fiddler设置过滤你就这样做，一做一个不只声！

fiddler设置过滤 基本的过滤操作流程以百度为例 步骤&#xff1a; 1、右侧高级工具栏点击Filters》勾选Use Filters》选择Show only Internet Hosts和Show only the following Hosts》在文本框中输入host地址 2、点击Changes not yet saved》再点击Actions》Run Filterset …
阅读更多...
如何获取高质量的静态住宅IP代理？常见误区与注意事项

如何获取高质量的静态住宅IP代理？常见误区与注意事项

静态住宅IP代理在今天的网络营销领域扮演着至关重要的角色&#xff0c;静态住宅IP代理以其稳定性和高匿名性&#xff0c;为互联网业务提供了一个安全的执行环境。通过模拟真实用户的网络行为&#xff0c;这些IP代理降低了企业在网络营销活动中被识别和封禁的风险。它保护了企业…
阅读更多...
echarts修改tooltip默认的圆点图标为其他样式

echarts修改tooltip默认的圆点图标为其他样式

业务需求&#xff0c;默认是圆点&#xff0c;需要把线的由圆点改为线 红色线是理论&#xff0c;点是历史理论&#xff0c;绿色线是实际&#xff0c; 点是历史实际&#xff0c;在series里的顺序也是这样排的。 打印出来的params里的marker就是圆点&#xff0c;改这段代码就可以了…
阅读更多...
使用STM32 HAL库驱动光电传感器的设计和优化

使用STM32 HAL库驱动光电传感器的设计和优化

光电传感器在许多应用中起着重要的作用&#xff0c;例如自动计数、距离测量等。STM32微控制器和HAL库提供了丰富的功能和易于使用的接口&#xff0c;使得光电传感器的设计和优化变得更加便捷。本文将介绍如何使用STM32 HAL库驱动光电传感器的设计和优化&#xff0c;包括硬件设计…
阅读更多...
OpenCV | 傅里叶变换——低通滤波器与高通滤波器

OpenCV | 傅里叶变换——低通滤波器与高通滤波器

import cv2 #opencv 读取的格式是BGR import numpy as np import matplotlib.pyplot as plt #Matplotlib是RGB %matplotlib inline def cv_show(img,name):cv2.imshow(name,img)cv2.waitKey()cv2.destroyAllWindows() 傅里叶变换 傅里叶变换的作用 高频&#xff1a;变化剧烈…
阅读更多...
JAVA文件IO, File类, 字符流,字节流

JAVA文件IO, File类, 字符流,字节流

文章目录 文件IO1. File2. IO流2.1 字符流2.1.1 Reader2.1.2 Writer 2.2 字节流2.2.1 InputStream2.2.2 FileInputStream2.2.3 利用Scanner进行字符读取2.2.4 OutputStream 文件IO I: Input, 从硬盘往内存读数据 O: Output, 从内存往硬盘输出数据 1. File Java 中通过 java…
阅读更多...
解析d3dcompiler_47.dll缺失怎么修复，4种方法修复d3dcompiler_47.dll文件

解析d3dcompiler_47.dll缺失怎么修复，4种方法修复d3dcompiler_47.dll文件

d3dcompiler_47.dll缺失怎么修复&#xff1f;其实在我们使用计算机操作的过程中&#xff0c;有时会遇到一些由dll文件错误导致的问题&#xff0c;其中d3dcompiler_47.dll丢失就是这样一种。那么究竟d3dcompiler_47.dll缺失是什么意思&#xff0c;为何它会发生丢失&#xff0c;以…
阅读更多...
PWM占空比原理是什么，几个实例带你进一步了解

PWM占空比原理是什么，几个实例带你进一步了解

PWM : 即脉冲宽度调制(Pulse Width Modulation) 脉冲宽度调制是利用微处理器的数字输出来对模拟电路进行控制的一种非常有效的技术&#xff0c;广泛应用在从测量、通信到功率控制与变换及嵌入式领域的许多领域中。 PWM控制技术以其控制简单&#xff0c;灵活和动态响应好的优点而…
阅读更多...
【用unity实现100个游戏之17】从零开始制作一个类幸存者肉鸽(Roguelike)游戏4（附项目源码）

【用unity实现100个游戏之17】从零开始制作一个类幸存者肉鸽(Roguelike)游戏4（附项目源码）

文章目录 本节最终效果前言命中敌人闪白和击退效果敌人死亡效果等级 击杀数 经验绘制经验条显示等级和杀敌数游戏倒计时玩家血条参考源码完结 本节最终效果 前言 本节紧跟着上一篇&#xff0c;主要实现敌人受击死亡效果特效&#xff0c;主角等级、击杀数、经验、血条UI显示。 …
阅读更多...
手写promise A+、catch、finally、all、allsettled、any、race

手写promise A+、catch、finally、all、allsettled、any、race

目录 手写promise 同步版 1.Promise的构造方法接收一个executor()&#xff0c;在new Promise()时就立刻执行executor回调 2.executor()内部的异步任务被放入宏/微任务队列&#xff0c;等待执行 3.状态与结果的管理 状态只能变更一次 4.then()调用成功/失败回调 catch是…
阅读更多...
内测分发平台是否支持敏捷开发和持续集成？

内测分发平台是否支持敏捷开发和持续集成？

大家好&#xff0c;我是咕噜-凯撒。敏捷开发和持续集成是软件开发中非常重要的流程和方法。内测分发平台作为应用开发和测试的关键环节需要具备这种能力。下面我简单的介绍一下敏捷开发和持续集成和提供的功能。图片来源&#xff1a;news.gulufenfa.com 敏捷开发是一种迭代、协…
阅读更多...
Asp.net core WebApi 配置自定义swaggerUI和中文注释

Asp.net core WebApi 配置自定义swaggerUI和中文注释

1.创建asp.net core webApi项目 默认会引入swagger的Nuget包 <PackageReference Include"Swashbuckle.AspNetCore" Version"6.2.3" />2.配置基本信息和中文注释&#xff08;默认是没有中文注释的&#xff09; 2.1创建一个新的controller using Micr…
阅读更多...
SELinux(一) 简介

SELinux(一) 简介

首发公号&#xff1a;Rand_cs 前段时间的工作遇到了一些关于 SELinux 的问题&#xff0c;初次接触不熟悉此概念&#xff0c;导致当时配置策略时束手束脚&#xff0c;焦头烂额&#xff0c;为此去系统的学习了下 SELinux 的东西。聊 SELinux 之前&#xff0c;先来看看什么叫做访…
阅读更多...
Linux以nohup方式运行jar包

Linux以nohup方式运行jar包

1、在需要运行的jar包同级目录下建立启动脚本文件&#xff1a; 文件内容&#xff1a; #! /bin/bash #注意&#xff1a;必须有&让其后台执行&#xff0c;否则没有pid生成 jar包路径为绝对路径 nohup java -jar /usr/local/testDemo/jdkDemo-0.0.1-SNAPSHOT.jar >/us…
阅读更多...
C51--4G模块

C51--4G模块

EC03-DNC&#xff1a;4G通信模块 EC03-DNC 功能特点&#xff1a; 采用最新4G CAT1方案&#xff1b; 支持数据透明传输; 支持TCP、UDP 网络协议; 支持心跳包、注册包功能最大支持64个字节数&#xff1b; 支持MQTT协议&#xff0c;支持接入OneNet平台、百度云平台、阿里云平台的…
阅读更多...
微信小程序开发——项目开发入门

微信小程序开发——项目开发入门

版权声明 本文原创作者&#xff1a;谷哥的小弟作者博客地址&#xff1a;http://blog.csdn.net/lfdfhl 概述 本文重点介绍微信小程序开发者工具的下载与安装与项目开发入门。 下载开发者工具 请在官方网站下载微信小程序开发工具&#xff1b;图示如下&#xff1a; 请依据实际…
阅读更多...
解决electron-builder打包不成功只能输出tgz文件的问题

解决electron-builder打包不成功只能输出tgz文件的问题

现象&#xff1a; 对应项目里配的指令&#xff1a; 但就是死活不成功&#xff0c;只能输出tgz压缩文件。 最后一咬牙下载了官方的electron-quick-start拿来试试&#xff0c;结果还是一样。 一时间没想法了。 后来突然脑袋灵光一闪&#xff0c;去他妈的直接npx 执行看看&…
阅读更多...
Java线程通信

Java线程通信

线程通信 案例 package com.itheima.d4;public class ThreadTest {public static void main(String[] args) {Desk desk new Desk();//创建3个生产者线程new Thread(() -> {while (true) {desk.put();}}, "厨师1").start();new Thread(() -> {while (true) {…
阅读更多...
华为设备使用python实现文件自动保存下载

华为设备使用python实现文件自动保存下载

实验目的&#xff1a; 公司有一台CE12800的设备&#xff0c;管理地址为172.16.1.2&#xff0c;现在需要编写自动化脚本&#xff0c;STELNET实现设备的自动保存配置文件&#xff0c;使用SFTP实现设备的文件下载。 实验拓扑&#xff1a; 实验步骤&#xff1a; 步骤1&#xff1…
阅读更多...
Android flutter项目 启动优化实战（二）利用 App Startup 优化项目和使用flutterboost中的问题解决

Android flutter项目 启动优化实战（二）利用 App Startup 优化项目和使用flutterboost中的问题解决

背景 书接上回&#xff1a; Android flutter项目 启动优化实战&#xff08;一&#xff09;使用benchmark分析项目 已经分析出了问题: 1.缩短总时长&#xff08;解决黑屏问题、懒启动、优化流程&#xff09;、2.优化启动项&#xff08;使用App Startup&#xff09;、3.提升用…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023