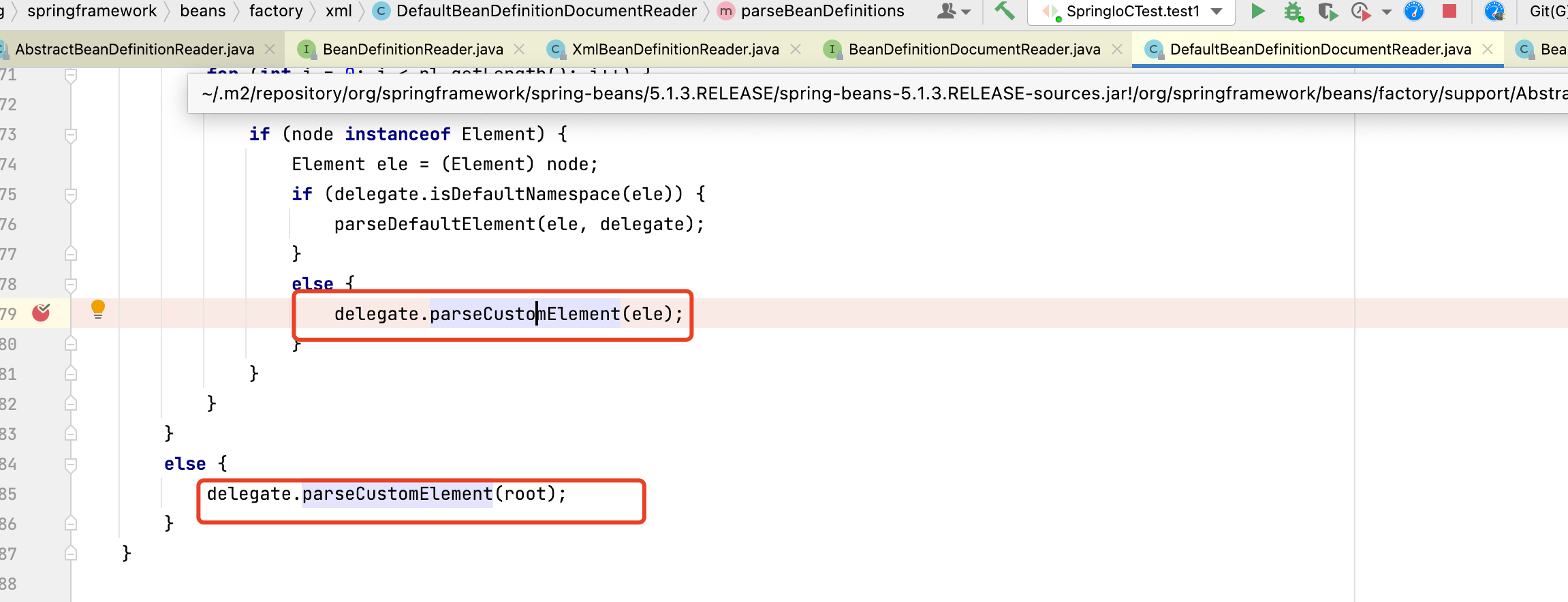
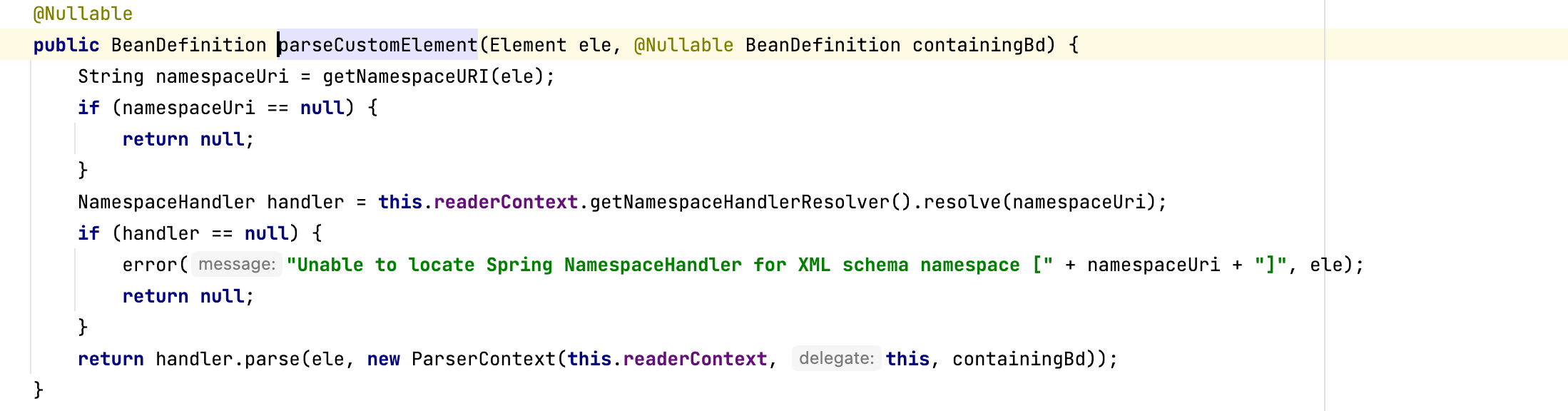
容易看出，Spring其实使用了一个Map了保存其映射关系，key就是命名空间的uri，value是NamespaceHandler对象或是Class完整名，如果发现是类名，那么用反射的方法进行初始化，如果是NamespaceHandler对象，那么直接返回。
NamespaceHandler映射关系来自于各个Spring jar包下的META-INF/spring.handlers文件，以spring-context包为例:

http\://www.springframework.org/schema/context=org.springframework.context.config.ContextNamespaceHandler
http\://www.springframework.org/schema/jee=org.springframework.ejb.config.JeeNamespaceHandler
http\://www.springframework.org/schema/lang=org.springframework.scripting.config.LangNamespaceHandler
http\://www.springframework.org/schema/task=org.springframework.scheduling.config.TaskNamespaceHandler
http\://www.springframework.org/schema/cache=org.springframework.cache.config.CacheNamespaceHandler

体系接口

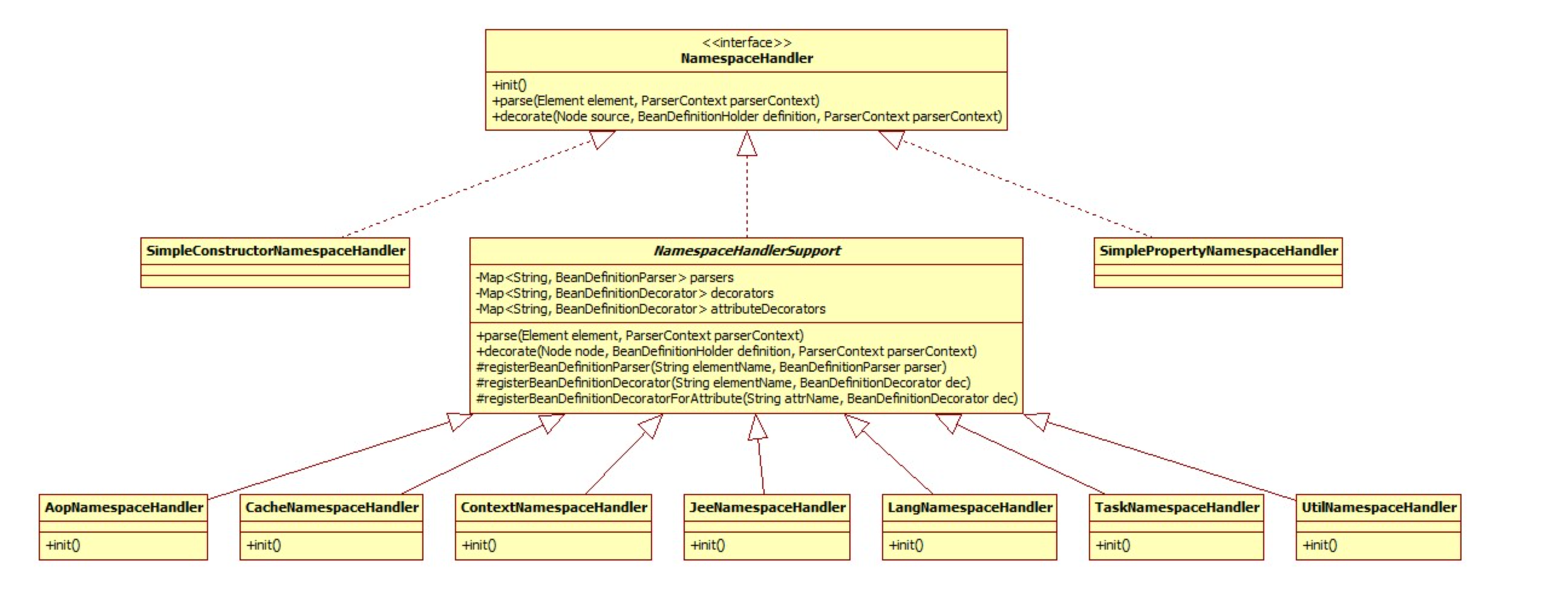
init
resolve中调用了其init方法，此方法用以向NamespaceHandler对象注册BeanDefinitionParser对象。此接口用以解析顶层(beans下)的非默认命名空间元素，比如<context:annotation-config />。
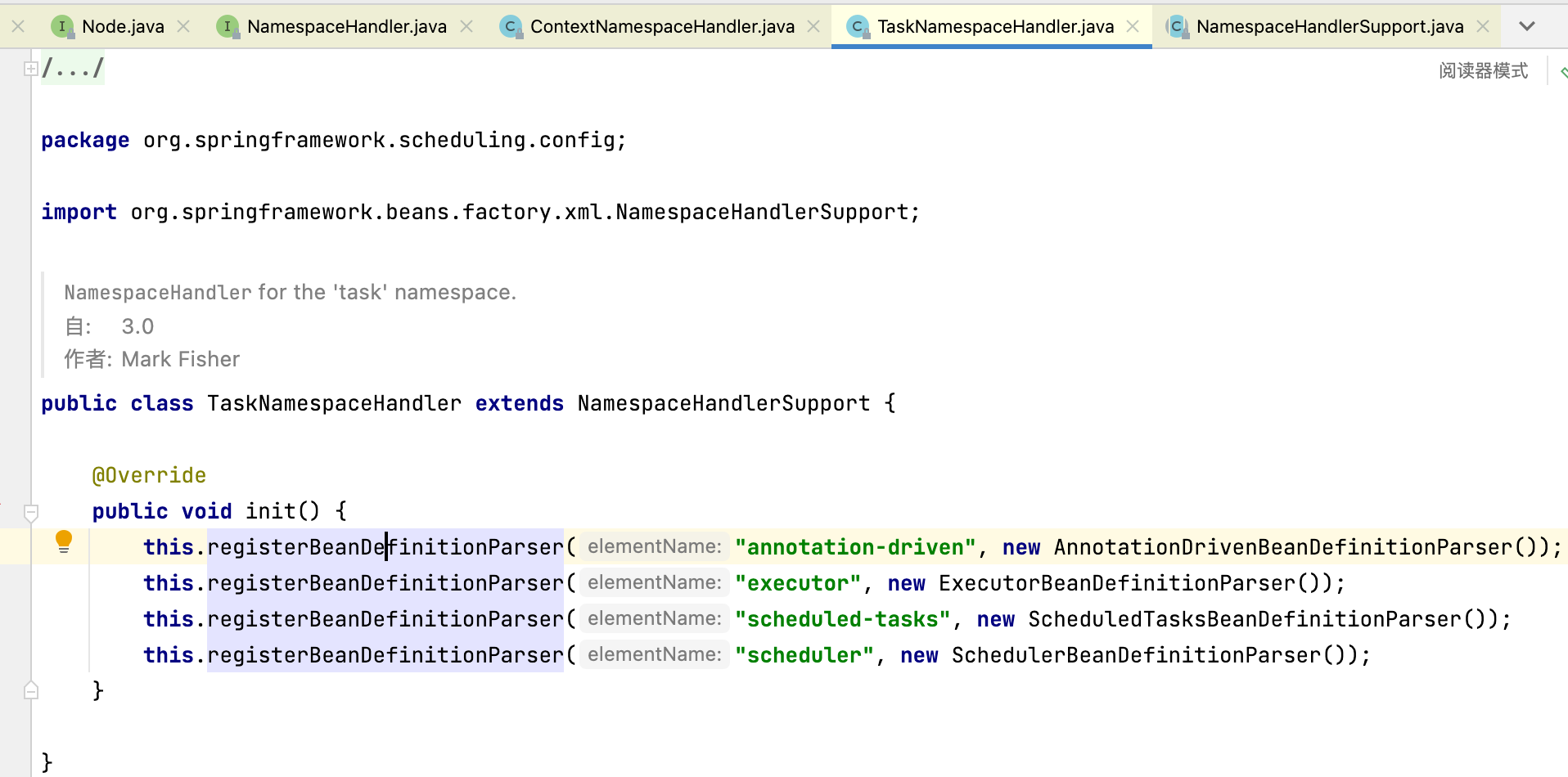
所以这样逻辑就很容易理解了: 每种子标签的解析仍是策略模式的体现，init负责向父类NamespaceHandlerSupport注册不同的策略，由父类的NamespaceHandlerSupport.parse方法根据具体的子标签调用相应的策略完成解析的过程。

如：