刷题前唠嗑

LeetCode？启动！！！

这个月第一次周末早起~

题目：二叉树中的伪回文路径

题目链接：1457. 二叉树中的伪回文路径

题目描述

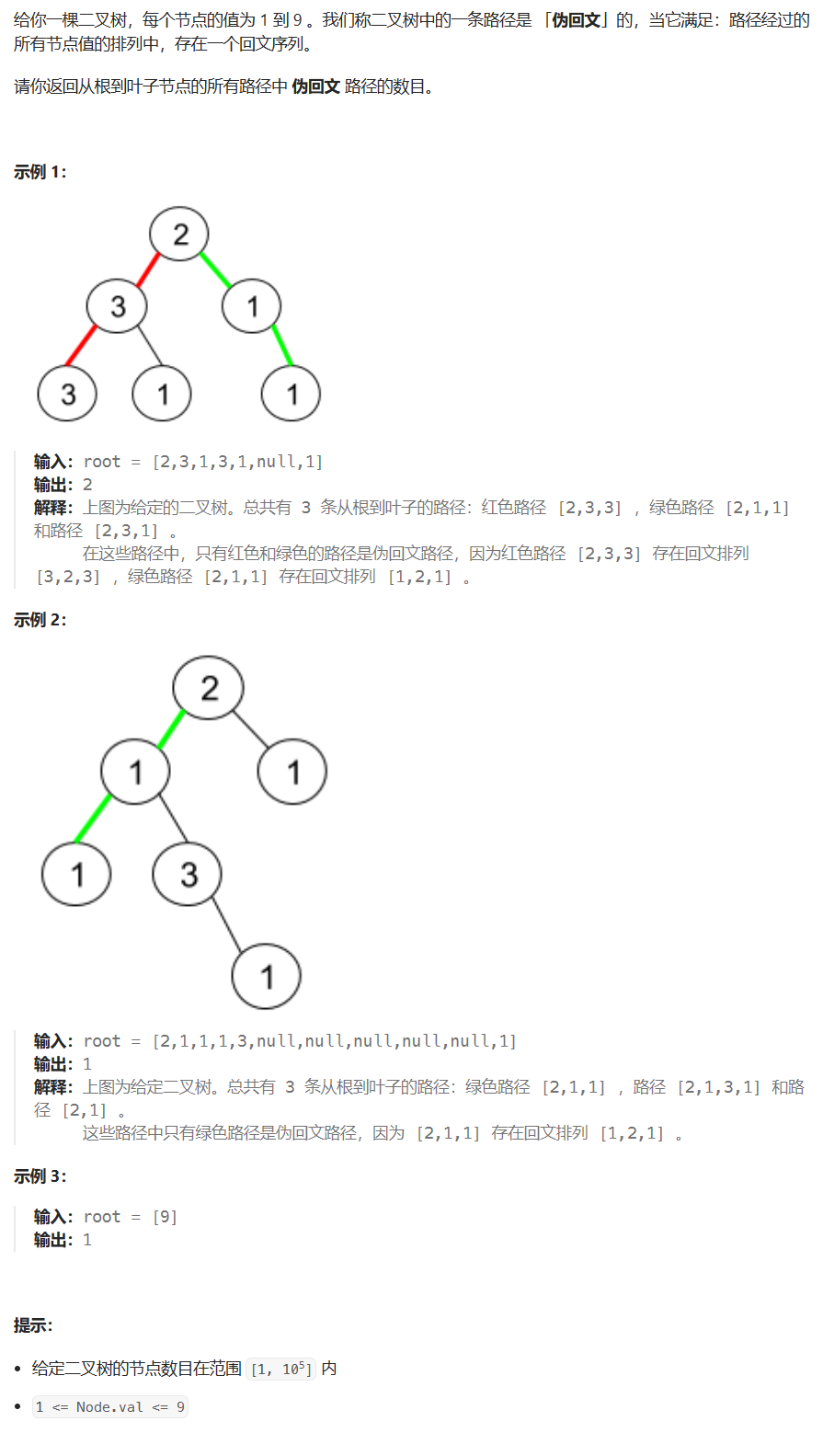
代码与解题思路

func pseudoPalindromicPaths (root *TreeNode) (ans int) {cnt := make([]int, 10)dfs(root, cnt, &ans)return ans
}func dfs(root *TreeNode, cnt []int, ans *int) {if root == nil {return}cnt[root.Val]++defer func() { cnt[root.Val]-- }()if root.Left == nil && root.Right == nil {if isFalsePalindromes(cnt) {*ans++}return}dfs(root.Left, cnt, ans)dfs(root.Right, cnt, ans)
}func isFalsePalindromes(cnt []int) bool { // 回文串最多只能存在一个奇数个数的值odd := 0for _, v := range cnt {if v%2 == 1 {odd++}}return odd <= 1
}

我做这道题的主要思路就是 dfs 搜索整个二叉树，在搜索的过程中用一个数组记录数字的出现情况，然后在走完一条路之后，判断是否是伪回文串，主要有两个需要注意的地方：

1. 如何判断是否是伪回文串？回文串只有两种可能，长度为奇数时，有一个值的个数是奇数，长度为偶数时，每个值的个数都是奇数。也就是只要数组中的值的个数是奇数的数量 <= 1 他就一定是伪回文串啦
2. 在使用数组进行计数的时候，当 dfs 回退到上一级的时候，计数需要 --，不然之前的计数会影响新一条路径的计数

偷看大佬题解

func pseudoPalindromicPaths(root *TreeNode) int {return dfs(root, 0)
}func dfs(root *TreeNode, mask int) int {if root == nil {return 0}mask ^= 1 << root.Val // 修改 root.Val 出现次数的奇偶性if root.Left == root.Right { // root 是叶子节点if mask&(mask-1) == 0 {return 1}return 0}return dfs(root.Left, mask) + dfs(root.Right, mask)
}

大佬的题解太妙了，具体思路是这样的：

1. 通过 10 个二进制位来表示这个十个数字，如果是值的数量是奇数则为 1，如果是偶数则为 0，这个是异或操作的结果
2. 通过 mask&(mask-1)，判断数量是奇数个的值有多少个，如果存在 1 个或者 0 个，使用 mask&(mask-1) 操作的结果就会等于 0，具体来说：如果是 mask 全为 0，& 任何数都为零（这就是存在 0 个数量的值是奇数的情况），如果是 mask 有一个位是 1，mask-1 这个操作会让一个 mask 中一个 1 的位置发生改变，也就是如果 mask 只存在一个 1，那使用 mask&(mask-1) 就会等于 0。（这就是存在 1 个数量的值是奇数的情况）

结语

学到了位运算的新用法