目录

题目：村村通

并查集 

题目：最小生成树

kruskal算法

prim算法

---

        

先引入问题：

要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

说白了就是将此图连通起来的最小代价。

        

对于一个有N个点的图，边一定是大于等于N-1条的。图的最小生成树，就是在这些边中选择N-1条出来，连接所有的N个点。这N-1条边的边权之和是所有方案中最小的

有两种算法：prim和kruskal

前者适合稠密图，后者适合稀疏图(不然炸你内存)

        

        

要先说并查集才行

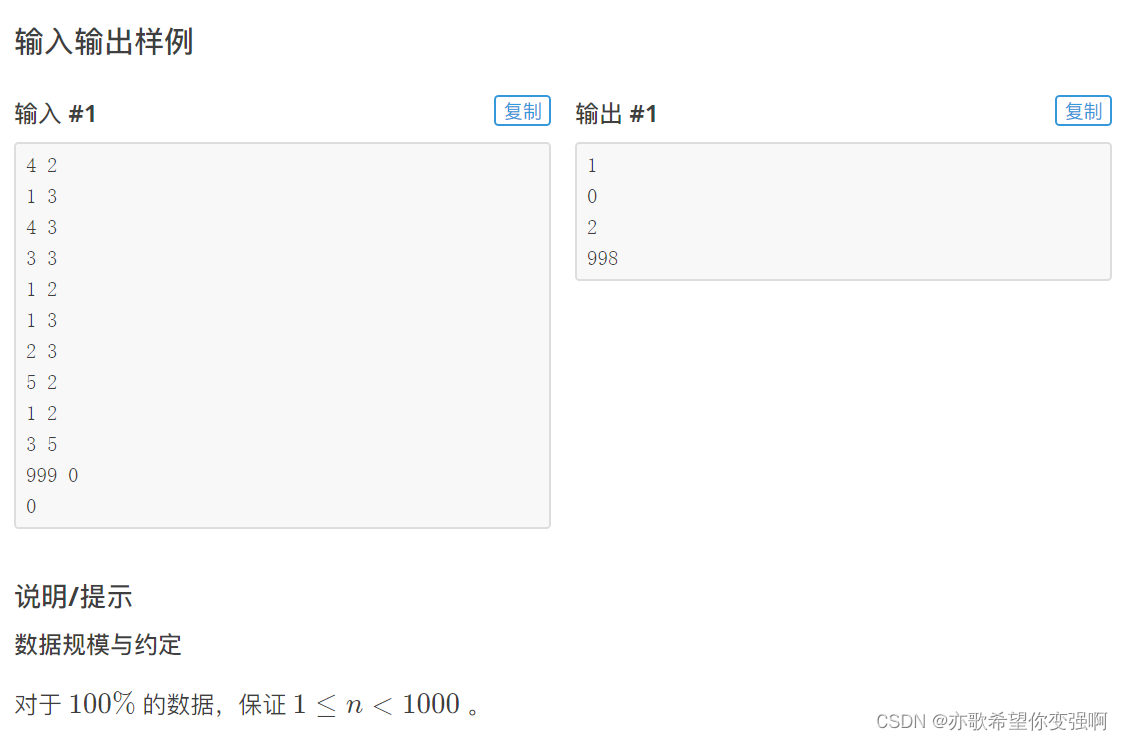
题目：村村通

        

并查集 

【并查集思想】：是集合。一个是并操作(建树)，一个是查操作(查树)。并操作是将一个集合的树变成另一个集合树的子树。

        
我们只需要建和原图等价的并查树即可，根本不用建原图
查操作是从该元素开始查找父节点直到找到根节点看看是否相同

        
1，初始化每个点的父亲为自身
2，并操作：(建边)合并两个集合的树根(祖宗)（查的过程中并路径压缩）
3，查操作：最后查找有几个祖宗即可

#include <bits/stdc++.h>              
using namespace std;
int fa[1000001], n, m, x, y;
int find(int x)
//找到祖先后并修改中间点的fa（路径压缩使更快的查到祖宗，
//其实就是对树进行优化，减少了树的深度，效果是将多代变成一代） 
{if(x!=fa[x]) fa[x]=find(fa[x]);
//自己不是祖宗，直接更新成亲爹的祖宗号
//但是如果是dp，那就要先保存原亲爹号，不然你就找不到爹了（路径压缩的代价）return fa[x];//返回祖先 
}
void unity(int x, int y)
{int f1=find(x);//如果x和y本来就在同一个集合完全 不影响int f2=find(y);fa[f1]=f2;//合并树根 
}
int main()
{while(true){int ans=0;cin>>n>>m;if(n==0) return 0;for(int i=1; i<=n; i++){fa[i]=i;//先初始化成节点}for(int i=1; i<=m; i++){scanf("%d %d", &x, &y);//合并<x,y>能到的地方unity(x,y);//建边,建树}for(int i=1; i<=n; i++){//一共有几个祖宗if(find(i)==i) ans++;}printf("%d\n", ans-1);//共需修ans-1条路即可}return 0;
}

         

         

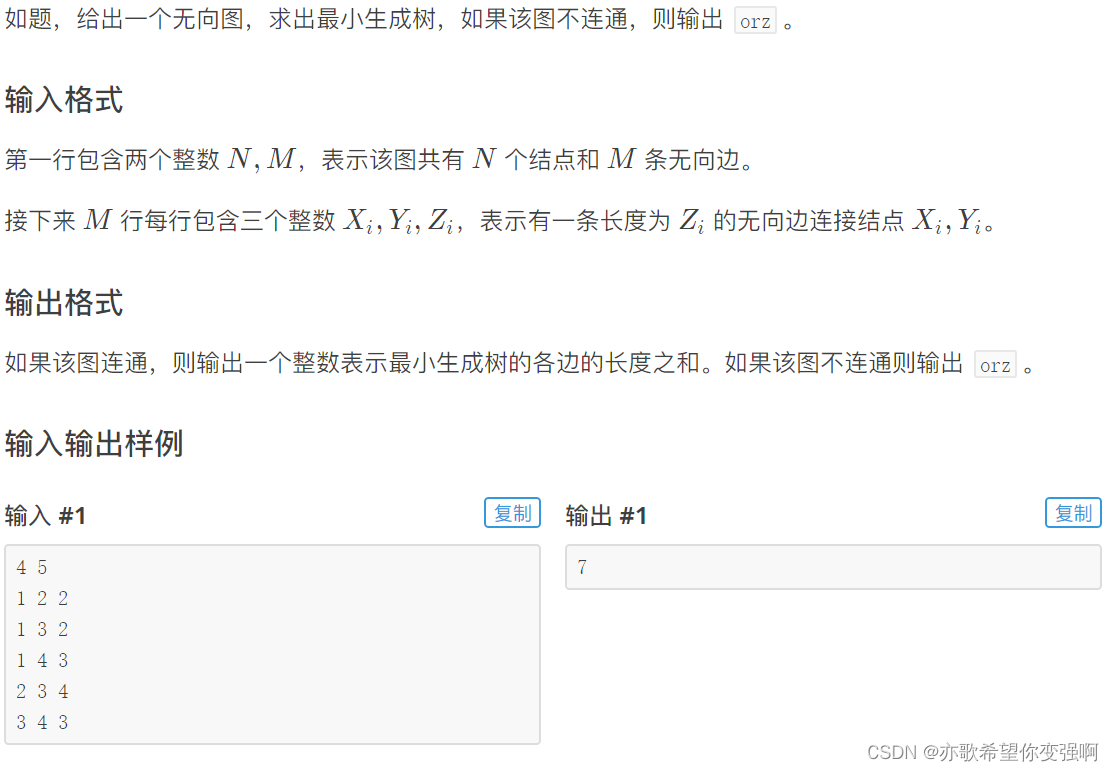
题目：最小生成树

         

kruskal算法

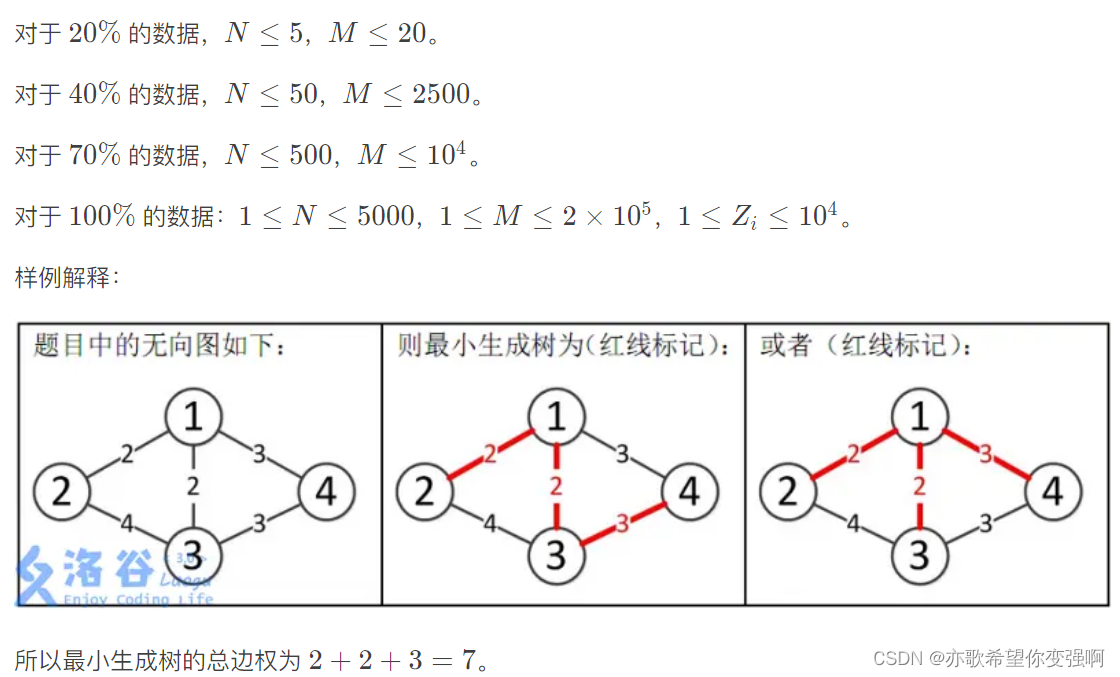
【kruskal】：贪心的每次取最小权值的边进行合并（只要不构成环），当恰好合并了n-1条边时候就是最小生成树。只要小于就不是，此图也不连通
可以使用并查集来实现合并和不构成环

                
kruskal甚至不需要建图，但是如果是完全图的话，存边容易MLE，这时候就要prim

#include<bits/stdc++.h>
using namespace std;
int f;
struct Edge{ int u,v,w; }e[200005];
int fa[5005],n,m,ans,cnt;bool cmp(Edge a,Edge b){ return a.w<b.w;}int find(int x)
{if(x!=fa[x]) fa[x]=find(fa[x]);return fa[x];//返回祖先 
}void kruskal()
{sort(e+1,e+1+m,cmp);//将边的权值排序for(int i=1;i<=m;i++){int fu=find(e[i].u), fv=find(e[i].v);if(fu==fv) continue;  //若出现两个点已经联通了，则说明这一条边不需要了ans+=e[i].w; //将此边权计入答案fa[fv]=fu; //合并操作if(++cnt==n-1)//如果边数恰好为n-1，则说明最小生成树已经建成{f=1;break;}}
}int main()
{cin>>n>>m;for(int i=1;i<=n;i++) fa[i]=i;//初始化并查集节点for(int i=1;i<=m;i++){scanf("%d %d %d",&e[i].u,&e[i].v,&e[i].w);}kruskal();if(f==1)printf("%d",ans);else cout<<"orz";//不连通return 0;
}

         

prim算法

【prim算法】：prim算法基于贪心，我们每次总是选出一个离生成树距离最小的点去加入生成树，最后实现最小生成树（不做证明，理解思想即可）

每次都最小生成数和dijkstra思想很像，都是从小图开始，每次都从周围合并一个最小的点然后不断扩大，所以长得也很像，感觉完全一样啊

#include <bits/stdc++.h>
using namespace std;
int k,n,m,cnt,sum;
int head[5005],dis[5005],vis[5005];
typedef pair <int,int> pii;
struct Edge{ int v,w,next;}e[400005];void add(int u,int v,int w){e[++k]=(Edge){v,w,head[u]};head[u]=k;}void prim()
{priority_queue <pii,vector<pii>,greater<pii> > q;memset(dis,0x3f,sizeof(dis));dis[1]=0;//dis是周围点到集合的最小距离q.push(make_pair(0,1));while(!q.empty()&&cnt<n)//cnt是已经加入的点数{int d=q.top().first,u=q.top().second;//取出周围最小dis的点q.pop();if(vis[u]) continue;cnt++;sum+=d;vis[u]=1;//标记此点已经加入for(i=head[u];i;i=e[i].next){int ve=e[i].v,vw=e[i].w;//到集合最小距离就是权值if(vw<dis[ve])//如果变小就更新入队，以便获取最小的点dis[ve]=vw,q.push(make_pair(dis[ve],ve));}}
}int main()
{int u,v,w;scanf("%d%d",&n,&m);for(i=1;i<=m;i++){scanf("%d%d%d",&u,&v,&w);add(u,v,w);add(v,u,w);}prim();if (cnt==n)printf("%d",sum);else printf("orz");//如果小于n说明不连通
}