文心一言 VS 讯飞星火 VS chatgpt （144）-- 算法导论12.1 4题

四、用go语言，对于一棵有 n 个结点的树，请设计在 O(n)时间内完成的先序遍历算法和后序遍历算法。

我个人喜欢 灵小智 。

文心一言：

在 Go 语言中，我们可以使用递归来实现树的前序遍历和后序遍历。以下是实现这两种方法的代码。

首先，我们定义一个树节点的结构：

type TreeNode struct {  Val   int  Left  *TreeNode  Right *TreeNode  
}

接下来，我们实现前序遍历（根-左-右）：

func preOrderTraversal(root *TreeNode) {  if root == nil { // 空节点则返回  return  }  fmt.Println(root.Val) // 先打印根节点  preOrderTraversal(root.Left) // 然后遍历左子树  preOrderTraversal(root.Right) // 最后遍历右子树  
}

然后，我们实现后序遍历（左-右-根）：

func postOrderTraversal(root *TreeNode) {  if root == nil { // 空节点则返回  return  }  postOrderTraversal(root.Left) // 先遍历左子树  postOrderTraversal(root.Right) // 然后遍历右子树  fmt.Println(root.Val) // 最后打印根节点  
}

以上的前序遍历和后序遍历的时间复杂度都是 O(n)，其中 n 是树的节点数量。这是因为每个节点都会被访问一次，每个节点只会被访问一次。

在这里插入图片描述

在这里插入图片描述

讯飞星火，代码正常运行：

package mainimport "fmt"type TreeNode struct {Val   intLeft  *TreeNodeRight *TreeNode
}func preorderTraversal(root *TreeNode) []int {if root == nil {return []int{}}stack := []*TreeNode{root}res := []int{root.Val}for len(stack) > 0 {node := stack[len(stack)-1]stack = stack[:len(stack)-1]if node.Right != nil {stack = append(stack, node.Right)res = append(res, node.Right.Val)}if node.Left != nil {stack = append(stack, node.Left)res = append(res, node.Left.Val)}}return res
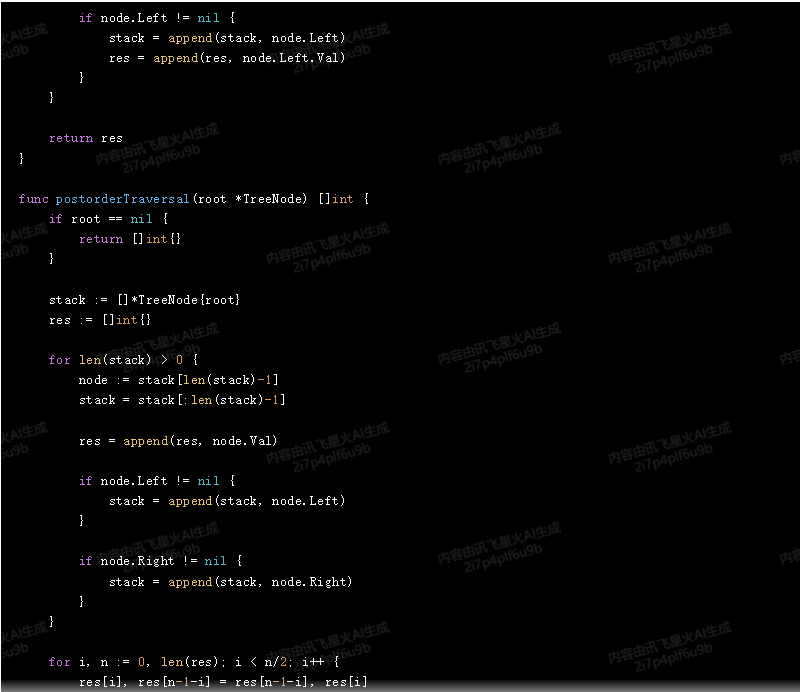
}func postorderTraversal(root *TreeNode) []int {if root == nil {return []int{}}stack := []*TreeNode{root}res := []int{}for len(stack) > 0 {node := stack[len(stack)-1]stack = stack[:len(stack)-1]res = append(res, node.Val)if node.Left != nil {stack = append(stack, node.Left)}if node.Right != nil {stack = append(stack, node.Right)}}for i, n := 0, len(res); i < n/2; i++ {res[i], res[n-1-i] = res[n-1-i], res[i]}return res
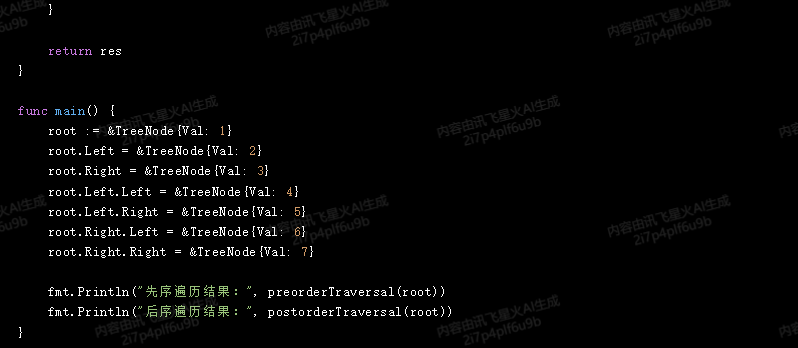
}func main() {root := &TreeNode{Val: 1}root.Left = &TreeNode{Val: 2}root.Right = &TreeNode{Val: 3}root.Left.Left = &TreeNode{Val: 4}root.Left.Right = &TreeNode{Val: 5}root.Right.Left = &TreeNode{Val: 6}root.Right.Right = &TreeNode{Val: 7}fmt.Println("先序遍历结果：", preorderTraversal(root))fmt.Println("后序遍历结果：", postorderTraversal(root))
}

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

360智脑，代码不能运行：

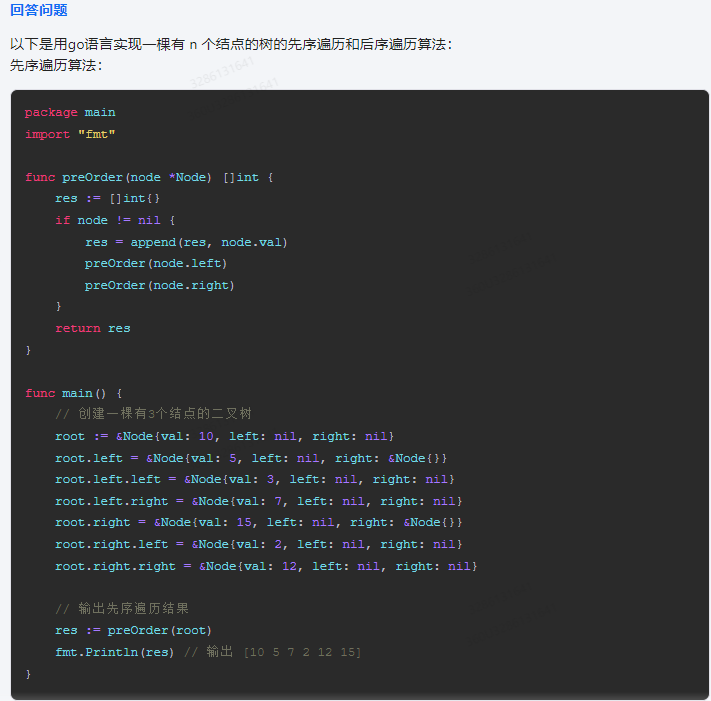
以下是用go语言实现一棵有 n 个结点的树的先序遍历和后序遍历算法：

先序遍历算法：

package main
import "fmt"func preOrder(node *Node) []int {res := []int{}if node != nil {res = append(res, node.val)preOrder(node.left)preOrder(node.right)}return res
}func main() {// 创建一棵有3个结点的二叉树root := &Node{val: 10, left: nil, right: nil}root.left = &Node{val: 5, left: nil, right: &Node{}}root.left.left = &Node{val: 3, left: nil, right: nil}root.left.right = &Node{val: 7, left: nil, right: nil}root.right = &Node{val: 15, left: nil, right: &Node{}}root.right.left = &Node{val: 2, left: nil, right: nil}root.right.right = &Node{val: 12, left: nil, right: nil}// 输出先序遍历结果res := preOrder(root)fmt.Println(res) // 输出 [10 5 7 2 12 15]
}

后序遍历算法：

package main
import "fmt"func postOrder(node *Node) []int {res := []int{}if node != nil {res = append(res, node.val)postOrder(node.left)postOrder(node.right)}return res
}func main() {// 创建一棵有3个结点的二叉树root := &Node{val: 10, left: nil, right: nil}root.left = &Node{val: 5, left: nil, right: nil}root.left.left = &Node{val: 3, left: nil, right: nil}root.left.right = &Node{val: 7, left: nil, right: nil}root.right = &Node{val: 15, left: nil, right: nil}root.right.left = &Node{val: 2, left: nil, right: nil}root.right.right = &Node{val: 12, left: nil, right: nil}// 输出后序遍历结果res := postOrder(root)fmt.Println(res) // 输出 [15 2 12 7 10 5 3 15]
}

在这里插入图片描述

在这里插入图片描述

智谱清言：

在 Go 语言中，可以使用递归或迭代方法实现树的遍历。以下是先序遍历和后序遍历的递归和迭代算法：

1.先序遍历算法：

递归算法：

func preOrderTraversalRecursive(root *TreeNode) []int {if root == nil {return []int{}}result := []int{root.Val}result = append(result, preOrderTraversalRecursive(root.Left)...)result = append(result, preOrderTraversalRecursive(root.Right)...)return result
}

迭代算法：

func preOrderTraversalIterative(root *TreeNode) []int {if root == nil {return []int{}}result := []int{}stack := []*TreeNode{root}for len(stack) > 0 {node := stack[len(stack)-1]stack = stack[:len(stack)-1]result = append(result, node.Val)if node.Right != nil {stack = append(stack, node.Right)}if node.Left != nil {stack = append(stack, node.Left)}}return result
}

2.后序遍历算法：

递归算法：

func postOrderTraversalRecursive(root *TreeNode) []int {if root == nil {return []int{}}result := postOrderTraversalRecursive(root.Left)result = append(result, root.Val)result = append(result, postOrderTraversalRecursive(root.Right)...)return result
}

迭代算法：

func postOrderTraversalIterative(root *TreeNode) []int {if root == nil {return []int{}}result := []int{}stack := []*TreeNode{root}for len(stack) > 0 {node := stack[len(stack)-1]stack = stack[:len(stack)-1]result = append(result, node.Val)if node.Left != nil {stack = append(stack, node.Left)}if node.Right != nil {stack = append(stack, node.Right)}}// Reverse the result array to get post-order traversalfor i, j := 0, len(result)-1; i < j; i, j = i+1, j-1 {result[i], result[j] = result[j], result[i]}return result
}

以上算法均能在 O(n) 时间内完成树的遍历。

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

通义千问：

这是一个经典的二叉树问题，我们可以使用深度优先搜索（DFS）来解决这个问题。

首先，我们需要定义一个树节点的数据结构：

type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode
}

然后，我们分别实现先序遍历和后序遍历的函数：

先序遍历：根 -> 左 -> 右

func preorderTraversal(root *TreeNode) []int {if root == nil {return []int{}}result := make([]int, 0)stack := []*TreeNode{root}for len(stack) > 0 {node := stack[len(stack)-1]result = append(result, node.Val)if node.Right != nil {stack = append(stack, node.Right)}if node.Left != nil {stack = append(stack, node.Left)} else {stack = stack[:len(stack)-1]}}return result
}

后序遍历：左 -> 右 -> 根

func postorderTraversal(root *TreeNode) []int {if root == nil {return []int{}}result := make([]int, 0)stack := []*TreeNode{root}prev := rootfor len(stack) > 0 {node := stack[len(stack)-1]if node.Left == nil && node.Right == nil || node == prev {result = append([]int{node.Val}, result...)prev = nodestack = stack[:len(stack)-1]} else if node.Right != nil {stack = append(stack, node.Right)} else {stack = stack[:len(stack)-1]if node.Left != nil {stack = append(stack, node.Left)}}}return result
}

这两种方法的时间复杂度都是O(n)，其中n是树中节点的数量，因为我们只需要遍历一次所有的节点。空间复杂度也是O(n)，因为在最坏的情况下，我们可能需要将所有的节点都压入栈中。

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

天工：

先序遍历算法：

先序遍历是指先访问根节点，然后依次访问左子树和右子树。在 Go 语言中，可以使用递归实现先序遍历算法。具体实现如下：

// 定义一个树节点结构体
type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode
}// 先序遍历算法
func PreorderTraversal(root *TreeNode) {if root == nil {return}// 访问当前节点fmt.Printf("%d ", root.Val)// 递归访问左右子树PreorderTraversal(root.Left)PreorderTraversal(root.Right)
}

后序遍历算法：

后序遍历是指先访问左子树，然后访问右子树，最后访问根节点。在 Go 语言中，可以使用递归实现后序遍历算法。具体实现如下：

// 定义一个树节点结构体
type TreeNode struct {Val intLeft *TreeNodeRight *TreeNode
}// 后序遍历算法
func PostorderTraversal(root *TreeNode) {if root == nil {return}// 递归访问左右子树PostorderTraversal(root.Left)PostorderTraversal(root.Right)// 访问当前节点fmt.Printf("%d ", root.Val)
}

以上两个算法都是使用递归实现的，时间复杂度为 O(n)，空间复杂度为 O(h)，其中 h 是树的高度。

在这里插入图片描述

在这里插入图片描述

灵小智，代码正常运行：

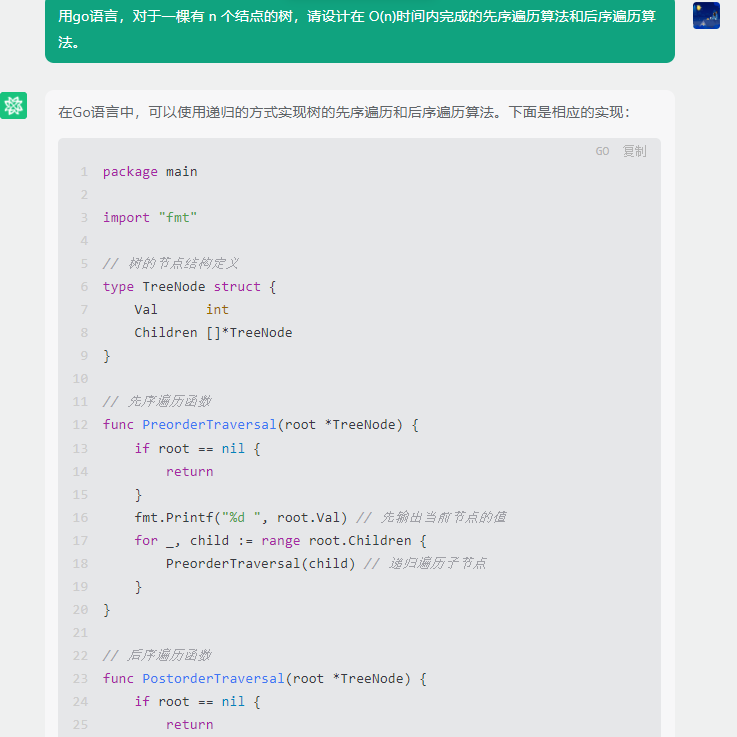
在Go语言中，可以使用递归的方式实现树的先序遍历和后序遍历算法。下面是相应的实现：

package mainimport "fmt"// 树的节点结构定义
type TreeNode struct {Val      intChildren []*TreeNode
}// 先序遍历函数
func PreorderTraversal(root *TreeNode) {if root == nil {return}fmt.Printf("%d ", root.Val) // 先输出当前节点的值for _, child := range root.Children {PreorderTraversal(child) // 递归遍历子节点}
}// 后序遍历函数
func PostorderTraversal(root *TreeNode) {if root == nil {return}for _, child := range root.Children {PostorderTraversal(child) // 递归遍历子节点}fmt.Printf("%d ", root.Val) // 最后输出当前节点的值
}func main() {// 构建一个示例树root := &TreeNode{Val: 1}node2 := &TreeNode{Val: 2}node3 := &TreeNode{Val: 3}node4 := &TreeNode{Val: 4}node5 := &TreeNode{Val: 5}root.Children = []*TreeNode{node2, node3, node4}node2.Children = []*TreeNode{node5}// 先序遍历fmt.Println("Preorder Traversal:")PreorderTraversal(root)fmt.Println()// 后序遍历fmt.Println("Postorder Traversal:")PostorderTraversal(root)fmt.Println()
}

以上代码通过先序遍历和后序遍历的方式遍历了一棵示例树，并输出了遍历结果。请注意，这里的先序遍历和后序遍历算法的时间复杂度为 O(n)，其中 n 是树中节点的个数。

在这里插入图片描述

在这里插入图片描述

chatgpt，代码正常运行：

在Go语言中，可以使用迭代的方式来实现树的先序遍历和后序遍历，以保证时间复杂度为O(n)。以下是示例代码：

package mainimport ("fmt"
)// 树节点结构体
type Node struct {Value intLeft  *NodeRight *Node
}// 先序遍历
func PreorderTraversal(root *Node) {if root == nil {return}stack := []*Node{root}for len(stack) > 0 {node := stack[len(stack)-1]stack = stack[:len(stack)-1]fmt.Printf("%d ", node.Value)if node.Right != nil {stack = append(stack, node.Right)}if node.Left != nil {stack = append(stack, node.Left)}}
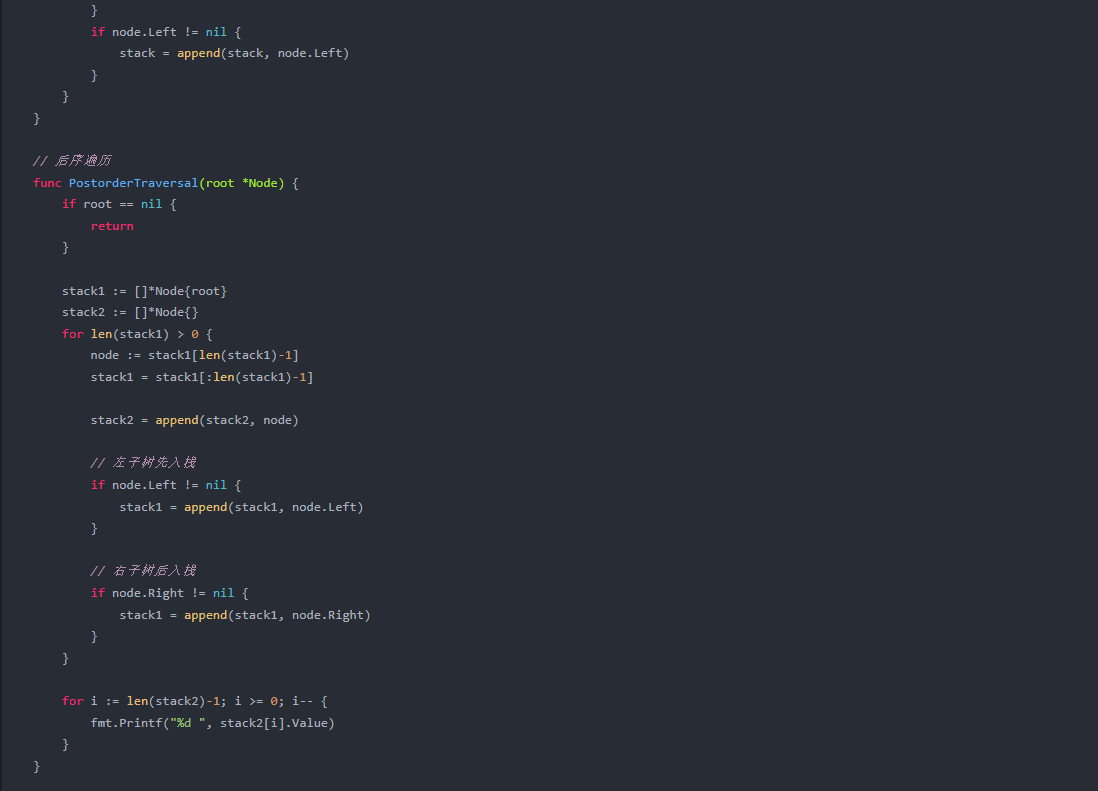
}// 后序遍历
func PostorderTraversal(root *Node) {if root == nil {return}stack1 := []*Node{root}stack2 := []*Node{}for len(stack1) > 0 {node := stack1[len(stack1)-1]stack1 = stack1[:len(stack1)-1]stack2 = append(stack2, node)// 左子树先入栈if node.Left != nil {stack1 = append(stack1, node.Left)}// 右子树后入栈 if node.Right != nil {  stack1 = append(stack1, node.Right)}  }for i := len(stack2)-1; i >= 0; i-- {  fmt.Printf("%d ", stack2[i].Value)}
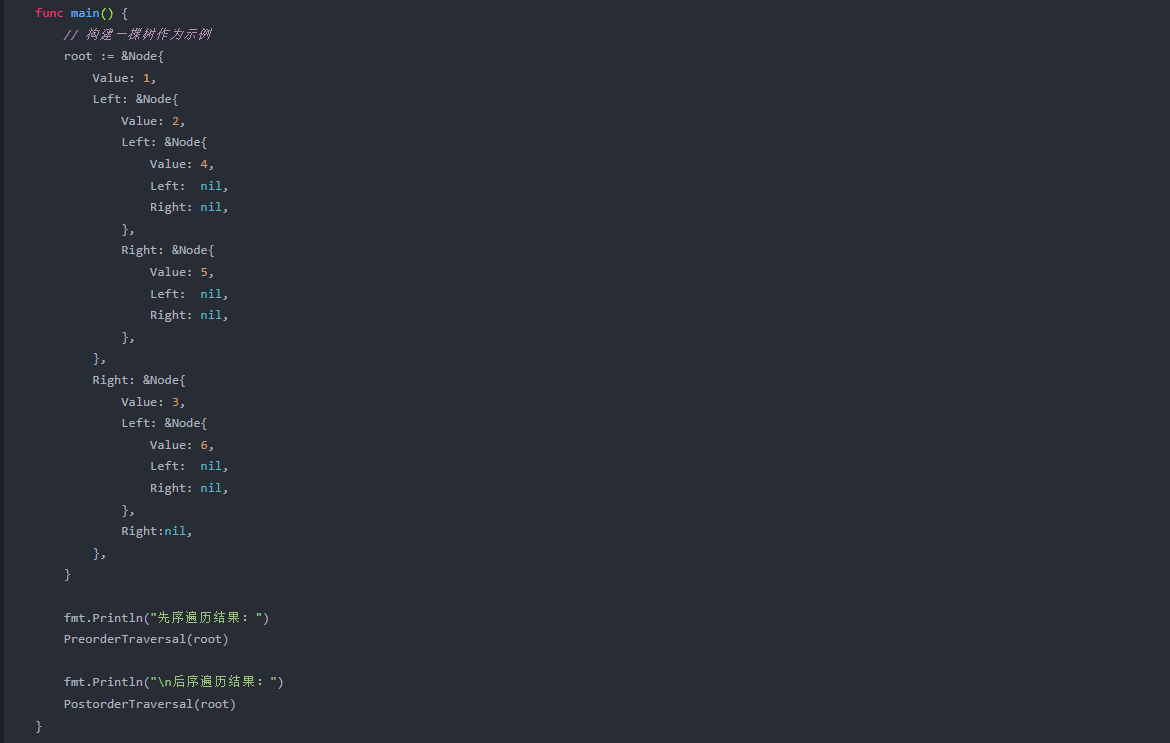
}func main() {// 构建一棵树作为示例root := &Node{Value: 1,Left: &Node{Value: 2,Left: &Node{Value: 4,Left:  nil,Right: nil,},Right: &Node{Value: 5,Left:  nil,Right: nil,},},Right: &Node{Value: 3,Left: &Node{Value: 6,Left:  nil,Right: nil,},Right:nil,   },}fmt.Println("先序遍历结果：")PreorderTraversal(root)fmt.Println("\n后序遍历结果：")PostorderTraversal(root)
}

以上代码中，我们使用了两个栈来实现后序遍历。第一个栈用于模拟先序遍历，将右子节点先入栈，然后左子节点入栈。第二个栈用于保存逆向的结果，在第一个栈为空时，将第一个栈中的元素依次弹出并加入到第二个栈中，然后输出即为后序遍历结果。

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/173866.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

window环境搭建StarRocksFE节点

window环境搭建StarRocksFE节点

StarRocks部署–源码编译 前言 ​ 注意:本文借用了一些其他文章的一些截图&#xff0c;同时自己做了具体的编译步骤&#xff0c;添加了一些新的内容 ​ 目标&#xff1a; 编译StarRocks2.5.13版本FE节点代码&#xff0c;在本地window环境运行&#xff0c;可以访问到8030界面…
阅读更多...
UIkit-UIAlertContent

UIkit-UIAlertContent

简单Demo //注意&#xff01;&#xff01;&#xff01;必须放在viewController的viewDidAppear里面&#xff0c;viewDidLoad里面不行 - (void)viewDidAppear:(BOOL)animated {// 创建 UIAlertControllerUIAlertController *alertController [UIAlertController alertControll…
阅读更多...
YOLO的网络结构组成

YOLO的网络结构组成

YOLOv5的CSP结构是 将原输入分成两个分支&#xff0c;分别进行卷积操作使得通道数减半&#xff0c; 然后一个分支进行Bottleneck * N操作&#xff0c;然后concat两个分支&#xff0c;使得BottlenneckCSP的输入与输出是一样的大小&#xff0c;这样是为了让模型学习到更多的特征。…
阅读更多...
为什么你的团队不需要使用拉取请求 | IDCF

为什么你的团队不需要使用拉取请求 | IDCF

作者&#xff1a;Kief Morris 译者&#xff1a;冬哥 原文&#xff1a;https://infrastructure-as-code.com/book/2021/01/02/pull-requests.html 前 言 Github 引入了Pull Request拉取请求&#xff08;简称PR&#xff09;实践和相关的支持功能&#xff0c;使运行开源项目的人…
阅读更多...
NX二次开发UF_CURVE_create_arc_point_tangent_point 函数介绍

NX二次开发UF_CURVE_create_arc_point_tangent_point 函数介绍

文章作者&#xff1a;里海 来源网站&#xff1a;https://blog.csdn.net/WangPaiFeiXingYuan UF_CURVE_create_arc_point_tangent_point Defined in: uf_curve.h int UF_CURVE_create_arc_point_tangent_point(tag_t point1, tag_t tangent_object, tag_t point2, UF_CURVE_he…
阅读更多...
Temu要求提交RSL Report 铅镉或RSL-Phthalate邻苯报告如何办理

Temu要求提交RSL Report 铅镉或RSL-Phthalate邻苯报告如何办理

Temu要求提交RSL Report 铅镉或RSL-Phthalate邻苯报告如何办理 Temu要求提交RSL Report 铅镉或RSL-Phthalate邻苯报告如何办理 RSL Report是欧盟REACH法规要求的一种资质报告&#xff0c;旨在确保产品不含对人体有害的化学物质。在珠宝首饰行业中&#xff0c;RSL Report认证是…
阅读更多...
SpringCloudAlibaba微服务 【实用篇】| Nacos注册中心

SpringCloudAlibaba微服务 【实用篇】| Nacos注册中心

目录 一&#xff1a;Nacos注册中心 1. 认识和安装Nacos 2. Nacos快速入门 3. Nacos服务分级存储模型 ①Nacos服务分级存储模型 ②NacosRule负载均衡 ③根据权重负载均衡 4. Nacos环境隔离 二&#xff1a;Nacos和Eureka的对比 tips&#xff1a;前些天突然发现了一个巨…
阅读更多...
Linux：docker容器操作（4）

Linux：docker容器操作（4）

docker的基础操作 Linux&#xff1a;docker基础操作&#xff08;3&#xff09;-CSDN博客https://blog.csdn.net/w14768855/article/details/134616198?spm1001.2014.3001.5501 我这里准备了两个镜像 镜像加载到容器 docker create [选项] 镜像 运行的程序 -i 让容器的标准输…
阅读更多...
外汇天眼：嘿！他们说这个比赛有手就能赢，你敢不敢来试试？

外汇天眼：嘿！他们说这个比赛有手就能赢，你敢不敢来试试？

在外汇市场的波涛汹涌中&#xff0c;一场引人注目的模拟交易比赛正在悄然展开&#xff0c;参与者们纷纷聚焦&#xff0c;听所有获奖的参赛投资者们说&#xff1a;这个比赛有手就能赢&#xff0c;你敢不敢来试试&#xff1f; 比赛规则简单而富有挑战性。你只需在外汇天眼APP开通…
阅读更多...
安卓手机如何使用JuiceSSH连接内网的Linux虚拟机并实现远程访问？

安卓手机如何使用JuiceSSH连接内网的Linux虚拟机并实现远程访问？

文章目录 1. 安装openSSH2. 安装cpolar3. 远程SFTP连接配置4. 远程SFTP访问4. 配置固定远程连接地址 SFTP&#xff08;SSH File Transfer Protocol&#xff09;是一种基于SSH&#xff08;Secure Shell&#xff09;安全协议的文件传输协议。与FTP协议相比&#xff0c;SFTP使用了…
阅读更多...
期刊Neurocomputing为什么简称IJON？

期刊Neurocomputing为什么简称IJON？

在数据库dplp的引用bib页面&#xff0c;Neurocomputing被简写为ijon&#xff0c;以dblp中的最新一篇文章为例&#xff1a; article{DBLP:journals/ijon/LiYFZH24,author {Mingchen Li andHuiqun Yu andGuisheng Fan andZiyi Zhou andZijie Huang},title {Enhan…
阅读更多...
“文件批量改名专家：轻松自定义重命名并智能导出文件信息“

“文件批量改名专家：轻松自定义重命名并智能导出文件信息“

在日常工作中&#xff0c;处理大量文件时&#xff0c;往往需要一款得力的文件批量改名工具来协助我们高效、有序地进行文件管理。今天&#xff0c;我要向大家介绍一款强大的文件批量改名工具&#xff0c;它不仅支持统一自定义重命名&#xff0c;还能将相关信息导出到表格中&…
阅读更多...
借助arthas 性能调优全过程

借助arthas 性能调优全过程

使用 arthas 的trace 命令分析方法耗时瓶颈&#xff1a; 可以看出 bindReloadZoneTimeLimite 耗时最久&#xff0c; 通过分析Bind 底层&#xff0c;将业务粒度进行拆分&#xff0c;加入并发执行 再次使用arthas 追踪单个方法耗时时间&#xff1a; 核心耗时方法&#xff0c…
阅读更多...
Drupal Core 8 PECL YAML 反序列化任意代码执行漏洞（CVE-2017-6920）

Drupal Core 8 PECL YAML 反序列化任意代码执行漏洞（CVE-2017-6920）

漏洞描述 影响软件&#xff1a;Drupal方式&#xff1a;反序列化参考链接&#xff1a;CVE-2017-6920:Drupal远程代码执行漏洞分析及POC构造效果&#xff1a;任意代码执行 漏洞环境及利用 搭建docker环境 环境启动后&#xff0c;访问 将会看到drupal的安装页面&#xff0c;一路…
阅读更多...
vue 表格虚拟滚动

vue 表格虚拟滚动

1.使用vxetable实现 官网 问题&#xff1a; 实现了表格的虚拟滚动&#xff0c;但是单元格数据不自动换行了 &#xff0c;如下显示的... 然后在官网看到是这样的&#xff0c;那我不是白写。。。 解决&#xff1a; 1.包一层div2.再写个换行样式 <vxe-column field"s…
阅读更多...
个微协议开发/微信个人号二次开发/ipad协议/api接口

个微协议开发/微信个人号二次开发/ipad协议/api接口

E云管家&#xff0c;是完整的第三方服务平台&#xff0c;并基于IPAD协议8.0.37开发出的最新个微API服务框架。 你可以 通过API 实现 个性化微信功能 &#xff08;例云发单助手、社群小助手、客服系统、机器人等&#xff09;&#xff0c;用来自动管理微信消息。用户仅可一次对接…
阅读更多...
如何更好的设计测试用例，看完就懂了。。。

如何更好的设计测试用例，看完就懂了。。。

引言 测试用例设计的最基本要求&#xff1a;覆盖住所要测试的功能。这是再基本不过的要求了&#xff0c;但别看只是简单的一句话&#xff0c;要能够达到切实覆盖全面&#xff0c;需要对被测试产品功能的全面了解、明确测试范围(特别是要明确哪些是不需要测试的)、具备基本的测…
阅读更多...
EasyExcel生成多sheet页的excel

EasyExcel生成多sheet页的excel

一、controller层 ApiOperation(value "明细查询导出") PostMapping(value "/SummaryDetailExport") public void summaryDetailExport(RequestBody SearchDTO dto, HttpServletResponse response) throws IOException {reportService.deptPackagingSum…
阅读更多...
北邮22级信通院数电：Verilog-FPGA（11）第十一周实验（1）用JK触发器实现8421码十进制计数器

北邮22级信通院数电：Verilog-FPGA（11）第十一周实验（1）用JK触发器实现8421码十进制计数器

北邮22信通一枚~ 跟随课程进度更新北邮信通院数字系统设计的笔记、代码和文章 持续关注作者 迎接数电实验学习~ 获取更多文章&#xff0c;请访问专栏&#xff1a; 北邮22级信通院数电实验_青山如墨雨如画的博客-CSDN博客 目录 一.代码部分 1.1 JK_8421.v 1.2 JK_ff.v …
阅读更多...
2023亚马逊云科技re:Invent，与全球合作伙伴探索更多发展可能

2023亚马逊云科技re:Invent，与全球合作伙伴探索更多发展可能

一年一度的全球云计算、科技圈的狂欢“Party”又双叒叕要来了&#xff01;2023年11月27日&#xff0c;2023亚马逊云科技re:Invent正式向全球云计算从业者、合作伙伴发出邀请&#xff0c;相聚拉斯维加斯&#xff0c;共同开启一场创新探索之旅&#xff01; 全球合作伙伴相约拉斯维…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023