1.定义

二叉树（Binary Tree）是另一种树型结构。    

二叉树的特点：

1）每个结点至多只有两棵子树（即二叉树中不存在度大于2的结点）；

2）二叉树的子树有左右之分，其次序不能任意颠倒。    

二叉树的递归定义  

二叉树(BinaryTree)是n(n≥0)个结点的有限集。它或者是空集(n=0)，或者同时满足以下两个条件： 

(1) 有且仅有一个根结点；  

(2) 其余的结点分成两棵互不相交的左子树和右子树。

二叉树的抽象数据类型   ADT BinaryTree {  D、R、P   }

 二叉树与树有区别：树的子树没有顺序，但如果二叉树的根结点只有一棵子树，必须明确区分它是左子树还是右子树，因为两者将构成不同形态的二叉树。因此，二叉树不是树的特例。它们是两种不同的数据结构。

二叉树有5种基本形态：

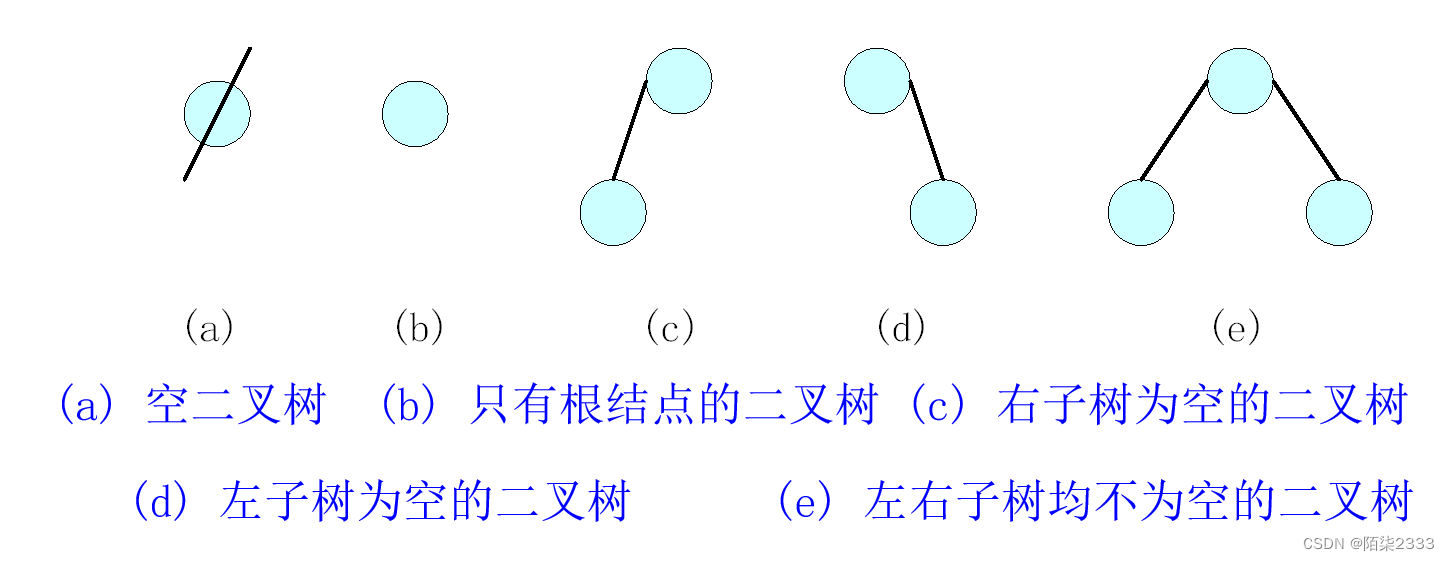
2.性质

性质1：若二叉树的层次从1开始, 则在二叉树的第 i 层最多有 2i-1 个结点。(i  1)

性质2：深度为k的二叉树至多有2k-1个结点（k>0）。

性质3：对于任何一棵二叉树，若度2的结点数有n2个，叶子结点数为n0，则n0=n2+1。

特例：

1）满二叉树：深度为k且有 2k-1个结点的二叉树。

特点：每一层上的结点数都是最大结点数。满二叉树不存在度数为1的节点，且树叶都在最下一层。可以对满二叉树的结点进行连续编号。

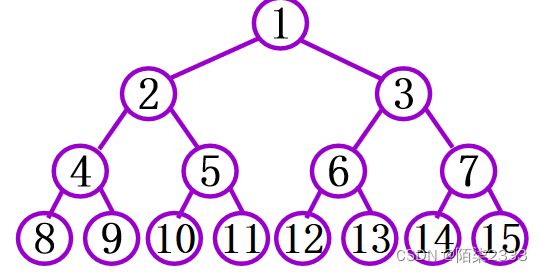
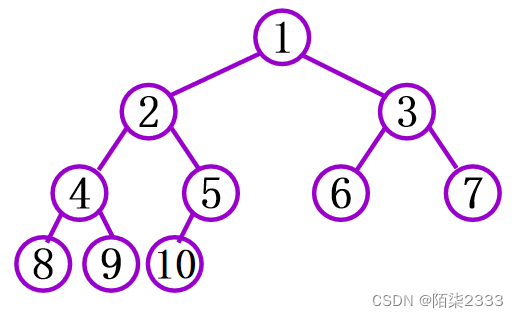
2）完全二叉树：深度为k，有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n 的结点一一对应时，称之为完全二叉树。

特点:

（1）叶子结点只可能在层次最大的两层上出现；              

（2）对任一结点，若其右分支下的子孙的最大层次为h，则其左分支下的子孙的最大层次数必为h或h+1。

对于特殊性质的二叉树，还具备以下2个性质：

性质4：具有n个结点的完全二叉树的深度必为log2n＋1。

性质5：如果对一棵有n个结点的完全二叉树(其深度为log2n＋1)的结点按层序编号，则对任一结点i（1≤i≤n），有：

1）如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲parent（i）是结点i/2 ；        

2）如果2i>n，则结点i无左孩子(结点i为叶子结点)；否则其 左孩子lchild（i）是结点2i；        

3）如果2i+1>n，则结点i无右孩子；否则其右孩子rchild(i) 是结点2i+1。

3.存储结构

1.顺序存储结构

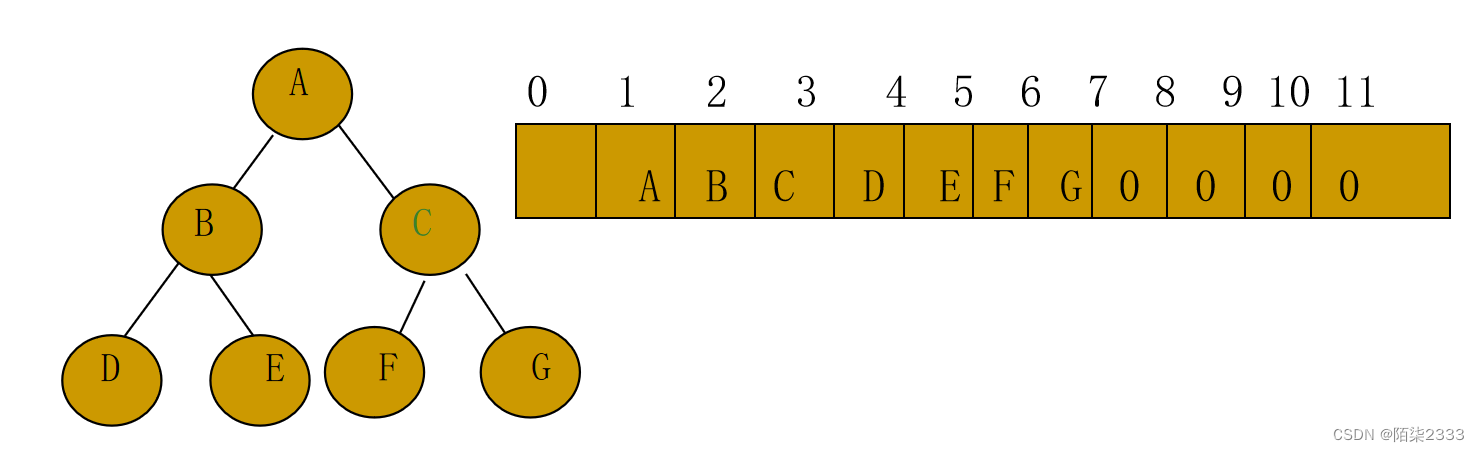
 二叉树的顺序存储，是采用一组连续的存储单元来存放二叉树中的结点，但是，由于二叉树是非线性结构，所以结点之间的逻辑关系难以从存储的先后确定。不过，由二叉树的性质5可知，对于完全二叉树，如果按照从上（根结点）到下（叶结点）和从左到右的顺序，对二叉树中的所有结点从0到n-1编号，这样存放到一维数组中。只要通过数组元素的下标关系，就可以确定二叉树中结点之间的逻辑关系。

#define  MAXSIZE  100	
typedef  int  ElemType;	
typedef struct wqbtree
{ElemType SequenBiTree[MAXSIZE];int n;		/*记录节点总数*/
}Fbitree;

对于一般的二叉树，如果仍采用顺序表示，首先要对它进行扩充，增加一些并不存在的空结点，使之成为一棵完全二叉树，然后再用一维数组顺序存储。

缺点：浪费存储空间。

完全二叉树用顺序存储结构，一般二叉树用链式存储结构。

2.链表存储结构

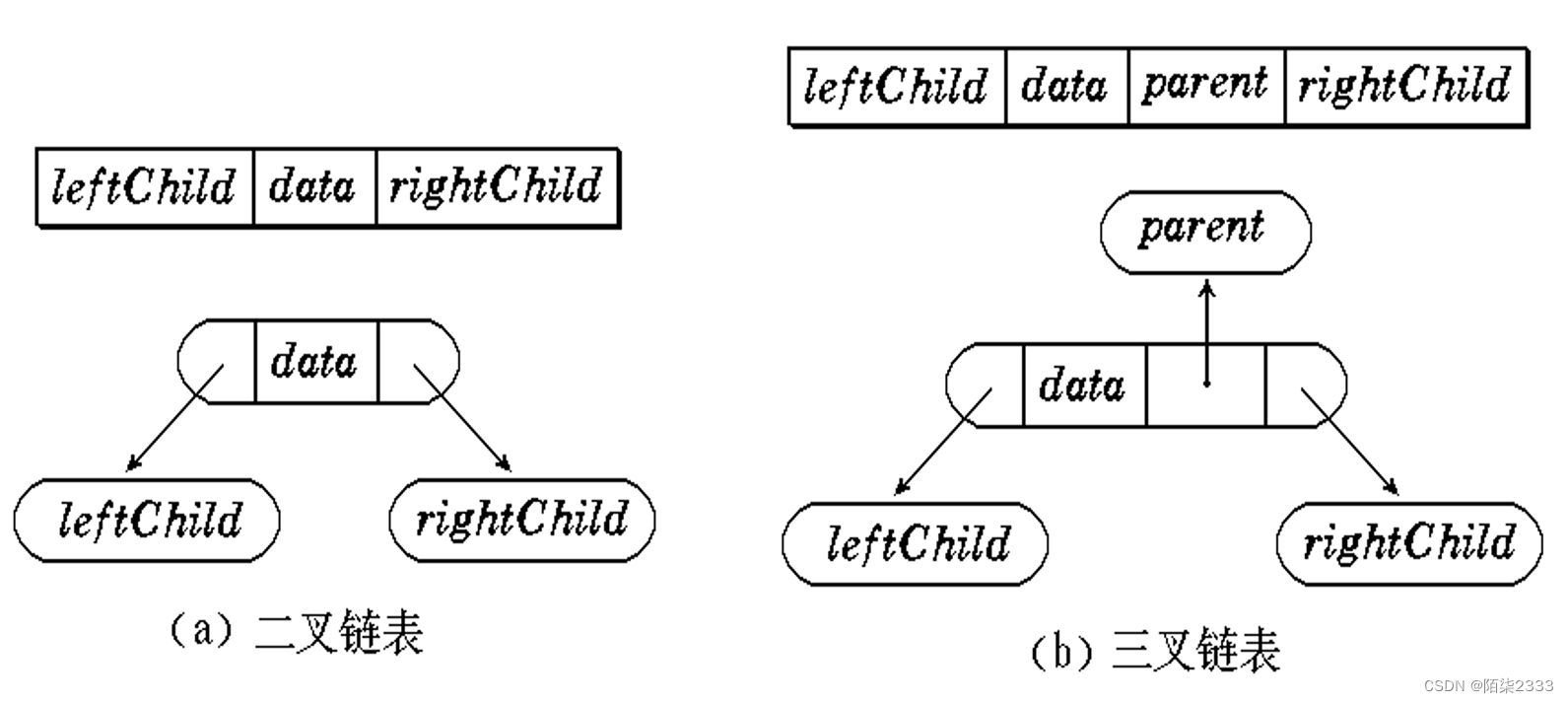
1.二叉链表

由于二叉树每个结点至多只有2个孩子，分别为左孩子和右孩子。因此可以把每个结点分成三个域：一个域存放结点本身的信息，另外两个是指针域，分别存放指向左、右孩子的指针。每个结点的结构表示为：

typedef  int  ElemType;	
typedef struct BiTreeNode
{ 	ElemType data;struct BiTreeNode *lchild, *rchild;
}BiTreeNode, *BiTree;

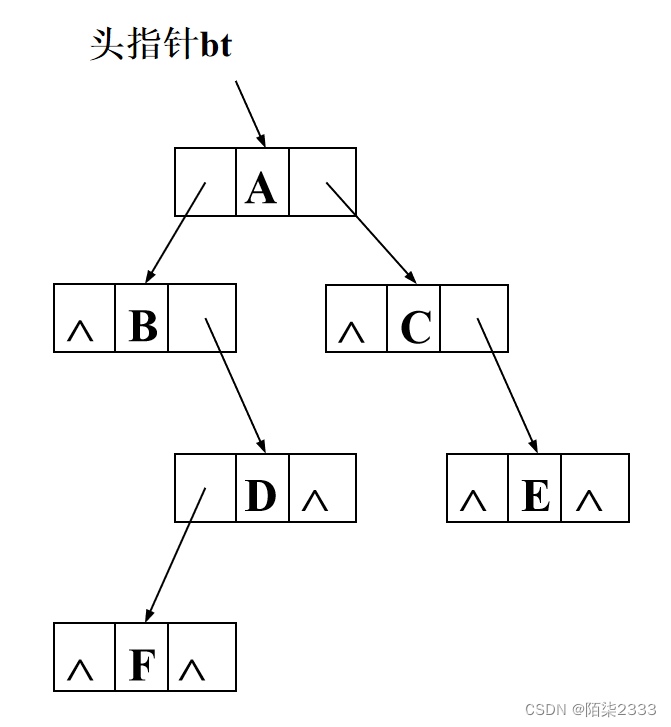
一个二叉链表由根指针root唯一确定。若二叉树为空，则root=NULL；若结点的某个孩子不存在，则相应的指针为空。 

具有n个结点的二叉链表中，共有2n个指针域。其中只有n-1个用来指示结点的左、右孩子，其余的n+1个指针域为空。

 若一个二叉树含有n个结点，则它的二叉链表中必含有2n个指针域， 其中必有n＋1个空的链域。

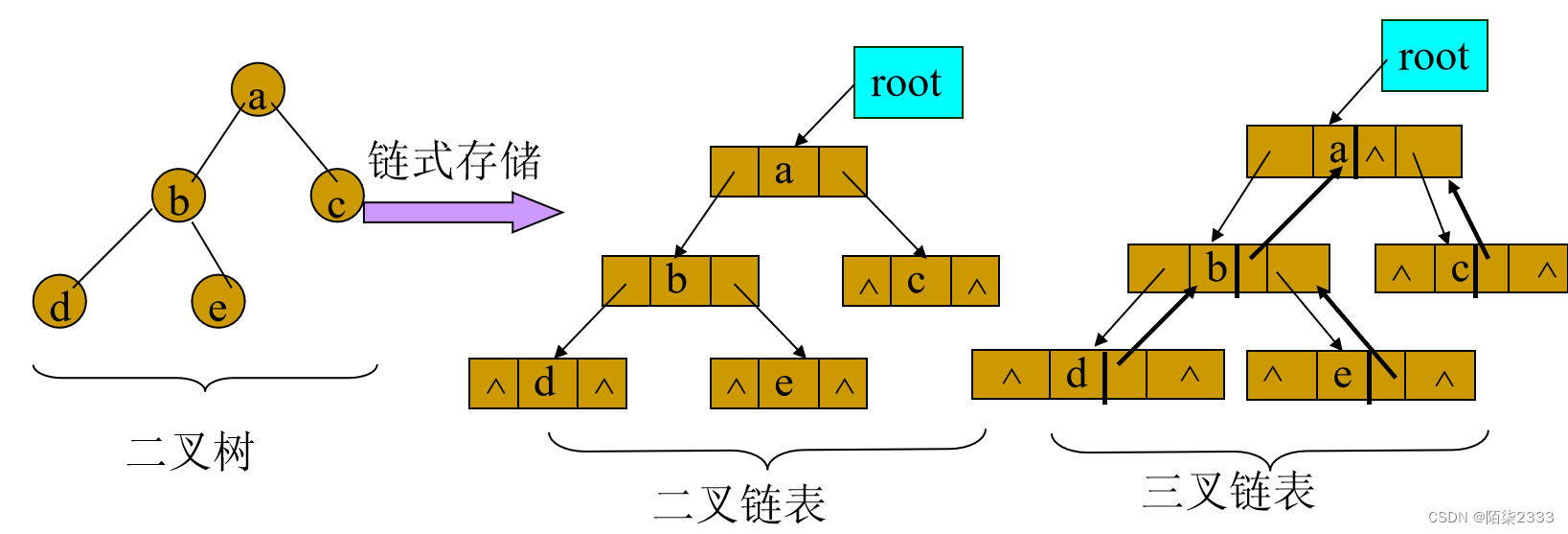
2.三叉链表

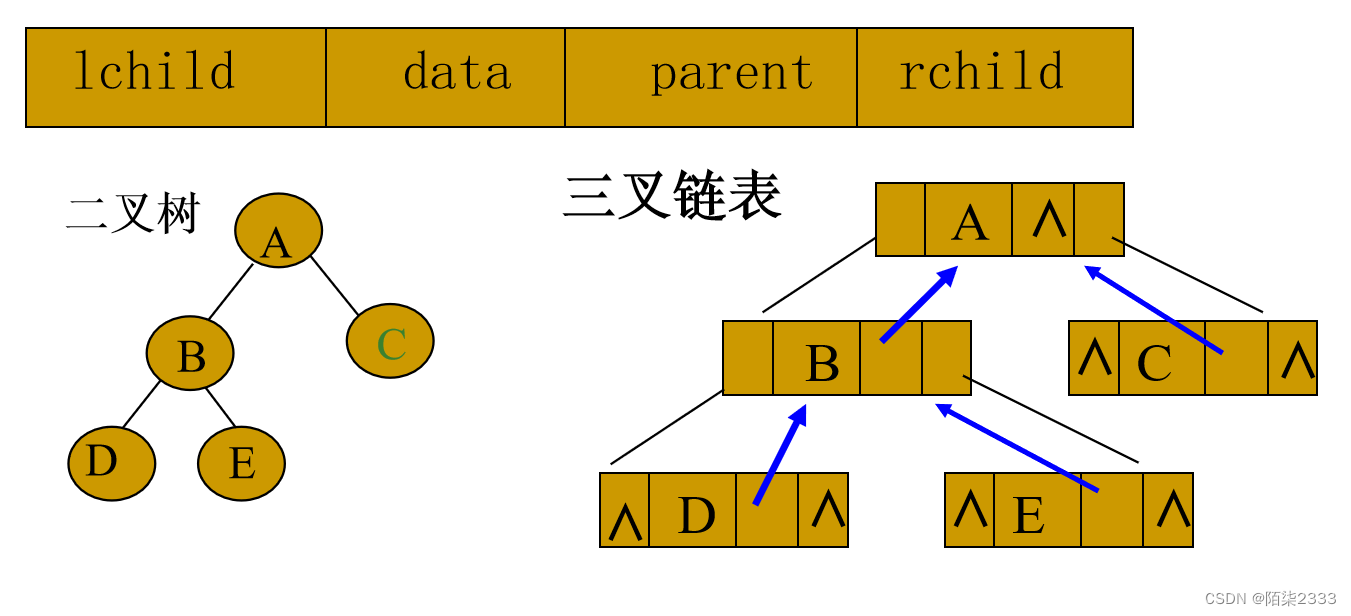
为了便于找到结点的双亲，可以在结点结构中增加一个指向其双亲结点的指针域，此时二叉链表变为三叉链表。 三叉链表的结点结构

typedef  int  ElemType;
typedef struct ThrTreeNode{ElemType data;struct ThrTreeNode  *lchild, *rchild，*parent；
}ThrTreeNode, *ThrTree;