学习率是最影响性能的超参数之一，如果我们只能调整一个超参数，那么最好的选择就是它。相比于其它超参数学习率以一种更加复杂的方式控制着模型的有效容量，当学习率最优时，模型的有效容量最大。本文从手动选择学习率到使用预热机制介绍了很多学习率的选择策略。

这篇文章记录了我对以下问题的理解：

• 学习速率是什么？学习速率有什么意义？
• 如何系统地获得良好的学习速率？
• 我们为什么要在训练过程中改变学习速率?
• 当使用预训练模型时，我们该如何解决学习速率的问题？

本文的大部分内容都是以 fast.ai 研究员写的内容 [1], [2], [5] 和 [3] 为基础的。本文是一个更为简洁的版本，通过本文可以快速获取这些文章的主要内容。如果您想了解更多详情，请参阅参考资料。

首先，什么是学习速率？

学习速率是指导我们该如何通过损失函数的梯度调整网络权重的超参数。学习率越低，损失函数的变化速度就越慢。虽然使用低学习率可以确保我们不会错过任何局部极小值，但也意味着我们将花费更长的时间来进行收敛，特别是在被困在高原区域的情况下。

下述公式表示了上面所说的这种关系。

1. new_weight = existing_weight — learning_rate * gradient

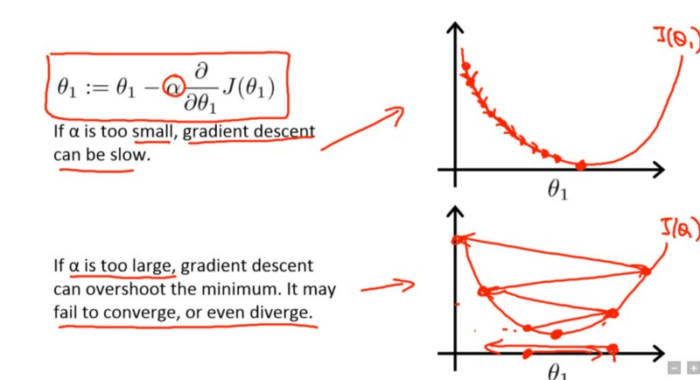
采用小学习速率（顶部）和大学习速率（底部）的梯度下降。来源：Coursera 上吴恩达（Andrew Ng）的机器学习课程。

一般而言，用户可以利用过去的经验（或其他类型的学习资料）直观地设定学习率的最佳值。

因此，想得到最佳学习速率是很难做到的。下图演示了配置学习速率时可能遇到的不同情况。

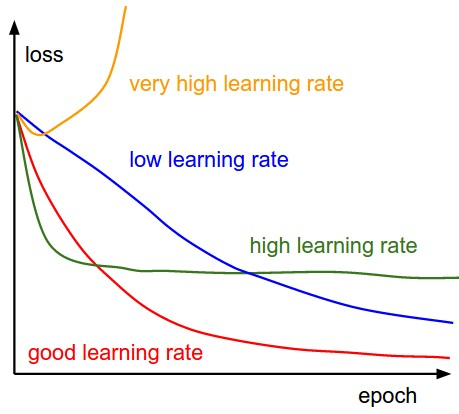
不同学习速率对收敛的影响（图片来源：cs231n）

此外，学习速率对模型收敛到局部极小值（也就是达到最好的精度）的速度也是有影响的。因此，从正确的方向做出正确的选择意味着我们可以用更短的时间来训练模型。

  
Less training time, lesser money spent on GPU cloud compute. 😃

有更好的方法选择学习速率吗？

在「训练神经网络的周期性学习速率」[4] 的 3.3 节中，Leslie N. Smith 认为，用户可以以非常低的学习率开始训练模型，在每一次迭代过程中逐渐提高学习率（线性提高或是指数提高都可以），用户可以用这种方法估计出最佳学习率。

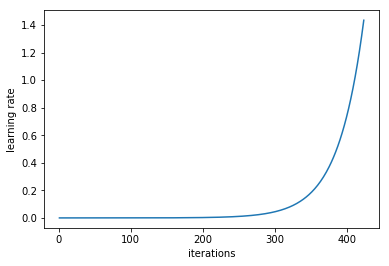
在每一个 mini-batch 后提升学习率

如果我们对每次迭代的学习进行记录，并绘制学习率（对数尺度）与损失，我们会看到，随着学习率的提高，从某个点开始损失会停止下降并开始提高。在实践中，学习速率的理想情况应该是从图的左边到最低点（如下图所示）。在本例中，是从 0.001 到 0.01。

上述方法看似有用，但该如何应用呢？

目前，上述方法在 fast.ai 包中作为一个函数进行使用。fast.ai 包是由 Jeremy Howard 开发的一种高级 pytorch 包（就像 Keras 之于 Tensorflow）。

在训练神经网络之前，只需输入以下命令即可开始找到最佳学习速率。

  
# learn is an instance of Learner class or one of derived classes like ConvLearner
learn.lr_find()
learn.sched.plot_lr()

使之更好

现在我们已经知道了什么是学习速率，那么当我们开始训练模型时，怎样才能系统地得到最理想的值呢。接下来，我们将介绍如何利用学习率来改善模型的性能。

传统的方法

一般而言，当已经设定好学习速率并训练模型时，只有等学习速率随着时间的推移而下降，模型才能最终收敛。

然而，随着梯度达到高原，训练损失会更难得到改善。在 [3] 中，Dauphin 等人认为，减少损失的难度来自鞍点，而不是局部最低点。

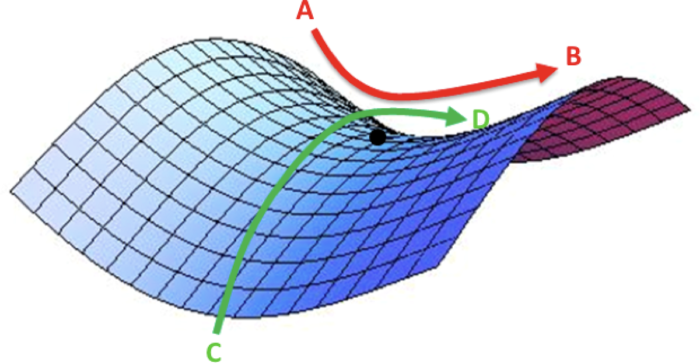
误差曲面中的鞍点。鞍点是函数上的导数为零但不是轴上局部极值的点。（图片来源：safaribooksonline）

所以我们该如何解决这个问题？

我们可以采取几种办法。[1] 中是这么说的：

…无需使用固定的学习速率，并随着时间的推移而令它下降。如果训练不会改善损失，我们可根据一些周期函数 f 来改变每次迭代的学习速率。每个 Epoch 的迭代次数都是固定的。这种方法让学习速率在合理的边界值之间周期变化。这是有益的，因为如果我们卡在鞍点上，提高学习速率可以更快地穿越鞍点。

在 [2] 中，Leslie 提出了一种「三角」方法，这种方法可以在每次迭代之后重新开始调整学习速率。

Leslie N. Smith 提出的「Triangular」和「Triangular2」学习率周期变化的方法。左图中，LR 的最小值和最大值保持不变。右图中，每个周期之后 LR 最小值和最大值之间的差减半。

另一种常用的方法是由 Loshchilov＆Hutter [6] 提出的预热重启（Warm Restarts）随机梯度下降。这种方法使用余弦函数作为周期函数，并在每个周期最大值时重新开始学习速率。「预热」是因为学习率重新开始时并不是从头开始的，而是由模型在最后一步收敛的参数决定的 [7]。

下图展示了伴随这种变化的过程，该过程将每个周期设置为相同的时间段。

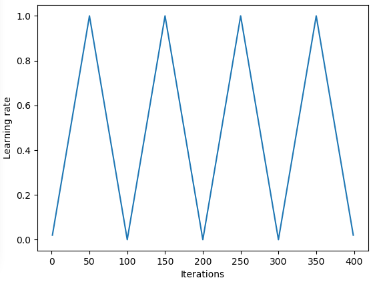
SGDR 图，学习率 vs 迭代次数。

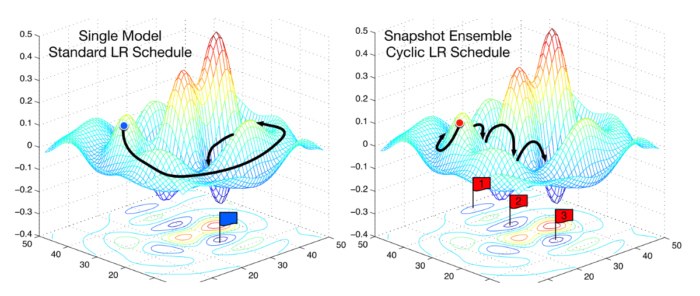
因此，我们现在可以通过周期性跳过「山脉」的办法缩短训练时间（下图）。

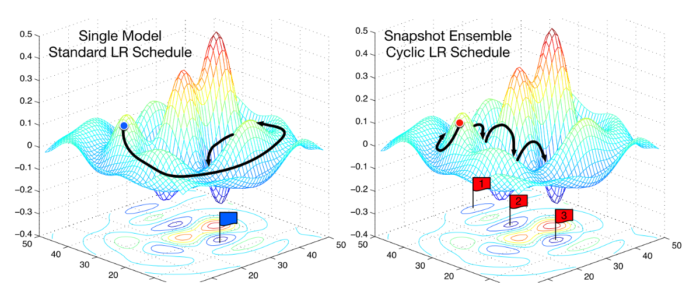
比较固定 LR 和周期 LR（图片来自 ruder.io）

研究表明，使用这些方法除了可以节省时间外，还可以在不调整的情况下提高分类准确性，而且可以减少迭代次数。

迁移学习中的学习速率

在 fast.ai 课程中，非常重视利用预训练模型解决 AI 问题。例如，在解决图像分类问题时，会教授学生如何使用 VGG 或 Resnet50 等预训练模型，并将其连接到想要预测的图像数据集。

我们采取下面的几个步骤，总结了 fast.ai 是如何完成模型构建（该程序不要与 fast.ai 包混淆）的：

1. 启用数据增强，precompute = True

2. 使用 lr_find() 找到损失仍在降低的最高学习速率

3. 从预计算激活值到最后一层训练 1~2 个 Epoch

4. 在 cycle_len = 1 的情况下使用数据增强（precompute=False）训练最后一层 2~3 次

5. 修改所有层为可训练状态

6. 将前面层的学习率设置得比下一个较高层低 3~10 倍

7. 再次使用 lr_find()

8. 在 cycle_mult=2 的情况下训练整个网络，直到过度拟合

从上面的步骤中，我们注意到步骤 2、5 和 7 提到了学习速率。这篇文章的前半部分已经基本涵盖了上述步骤中的第 2 项——如何在训练模型之前得出最佳学习率。

在下文中，我们会通过 SGDR 来了解如何通过重启学习速率来减少训练时间和提高准确性，以避免梯度接近零。

在最后一节中，我们将重点介绍差异学习（differential learning），以及如何在训练带有预训练模型中应用差异学习确定学习速率。

什么是差异学习

差异学习（different learning）在训练期间为网络中的不同层设置不同的学习速率。这种方法与人们常用的学习速率配置方法相反，常用的方法是训练时在整个网络中使用相同的学习速率。

在写这篇文章的时候，Jeremy 和 Sebastian Ruder 发表的一篇论文深入探讨了这个问题。所以我估计差异学习速率现在有一个新的名字——差别性的精调。😃

为了更清楚地说明这个概念，我们可以参考下面的图。在下图中将一个预训练模型分成 3 组，每个组的学习速率都是逐渐增加的。

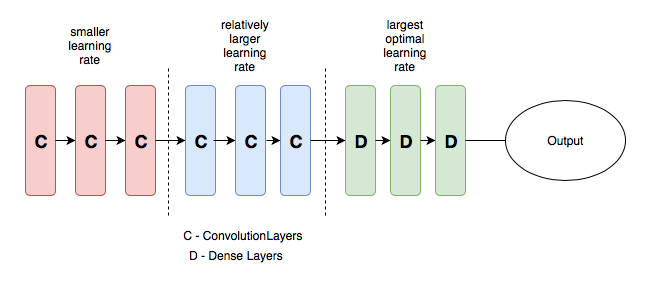
具有差异学习速率的简单 CNN 模型。图片来自 [3]

这种方法的意义在于，前几个层通常会包含非常细微的数据细节，比如线和边，我们一般不希望改变这些细节并想保留它的信息。因此，无需大量改变权重。

相比之下，在后面的层，以绿色以上的层为例，我们可以从中获得眼球、嘴巴或鼻子等数据的细节特征，但我们可能不需要保留它们。

这种方法与其他微调方法相比如何？

在 [9] 中提出，微调整个模型太过昂贵，因为有些模型可能超过了 100 层。因此人们通常一次一层地对模型进行微调。

然而，这样的调整对顺序有要求，不具并行性，且因为需要通过数据集进行微调，导致模型会在小数据集上过拟合。

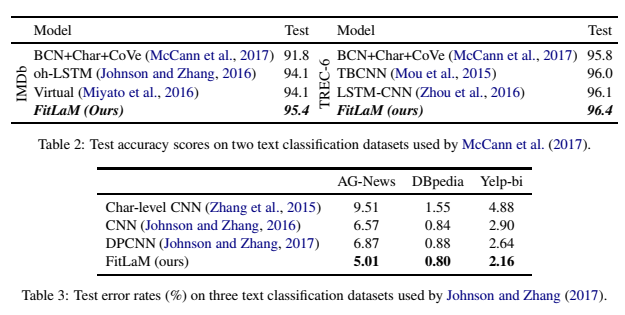
下表证明 [9] 中引入的方法能够在各种 NLP 分类任务中提高准确度且降低错误率。

参考文献：

[1] Improving the way we work with learning rate.

[2] The Cyclical Learning Rate technique.

[3] Transfer Learning using differential learning rates.

[4] Leslie N. Smith. Cyclical Learning Rates for Training Neural Networks.

[5] Estimating an Optimal Learning Rate for a Deep Neural Network

[6] Stochastic Gradient Descent with Warm Restarts

[7] Optimization for Deep Learning Highlights in 2017

[8] Lesson 1 Notebook, fast.ai Part 1 V2

[9] Fine-tuned Language Models for Text Classification

原文链接：https://towardsdatascience.com/understanding-learning-rates-and-how-it-improves-performance-in-deep-learning-d0d4059c1c10