前言
之前已经说过堆的特点了,具体文章在数据结构与算法【队列】的Java实现-CSDN博客。因此直接实现堆的其他功能。
建堆
所谓建堆,就是将一个初始的堆变为大顶堆或是小顶堆。这里以大顶堆为例。展示如何建堆。
- 找到最后一个非叶子节点
- 从后向前,对每个节点执行下潜
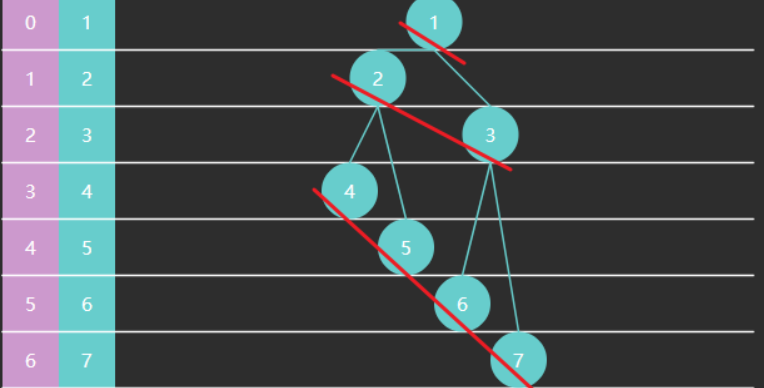
一些规律(0作为根节点时满足)
- 一棵满二叉树节点个数为 2^h-1,如下例中高度 h=3 节点数是 2^3-1=7
- 非叶子节点范围为 [0, size/2-1]
建堆的时间复杂度为O(n)。
一个基础的大顶堆实现代码如下
public class MaxHeap {int[] array;int size;public MaxHeap(int capacity) {this.array = new int[capacity];}public MaxHeap(int[] array) {this.array = array;this.size = array.length;heapify();}/*** 获取堆顶元素** @return 堆顶元素*/public int peek() {return array[0];}/*** 删除堆顶元素** @return 堆顶元素*/public int poll() {int top = array[0];swap(0, size - 1);size--;down(0);return top;}/*** 删除指定索引处元素** @param index 索引* @return 被删除元素*/public int poll(int index) {int deleted = array[index];up(Integer.MAX_VALUE, index);poll();return deleted;}/*** 替换堆顶元素** @param replaced 新元素*/public void replace(int replaced) {array[0] = replaced;down(0);}/*** 堆的尾部添加元素** @param offered 新元素* @return 是否添加成功*/public boolean offer(int offered) {if (size == array.length) {return false;}up(offered, size);size++;return true;}// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶private void up(int offered, int index) {int child = index;while (child > 0) {int parent = (child - 1) / 2;if (offered > array[parent]) {array[child] = array[parent];} else {break;}child = parent;}array[child] = offered;}// 建堆private void heapify() {// 如何找到最后这个非叶子节点 size / 2 - 1for (int i = size / 2 - 1; i >= 0; i--) {down(i);}}// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大private void down(int parent) {int left = parent * 2 + 1;int right = left + 1;int max = parent;if (left < size && array[left] > array[max]) {max = left;}if (right < size && array[right] > array[max]) {max = right;}if (max != parent) { // 找到了更大的孩子swap(max, parent);down(max);}}// 交换两个索引处的元素private void swap(int i, int j) {int t = array[i];array[i] = array[j];array[j] = t;}
}










保证一看就会)







