【数据结构-零基础学习】线索二叉树(代码+图示+解析)

文章目录

【数据结构-零基础学习】线索二叉树(代码+图示+解析)
@[toc]
定义
产生背景
种类
示意图
1)未加入线索的普通二叉树示意图1.1
2)线索添加的规则
3)中序线索二叉树示意图1.2
4)中序线索二叉树分析示意图1.3

设计代码逻辑(重点)
代码实现
ThreadedBinaryTree类
Test测试类
测试结果

优势

定义

线索二叉树是一种二叉树的数据结构，它的特点在于空闲指针用于指向节点在某种特定遍历方式下的前驱或后继。在传统的二叉树中，每个节点有两个指针，指向其左孩子和右孩子。如果任一孩子不存在，相应的指针便为空。线索二叉树利用这些空指针，存储指向遍历序列中前驱或后继的指针，从而增加遍历效率。

产生背景

线索二叉树产生的原因主要是为了提高二叉树的遍历效率。在未线索化的二叉树中，遍历元素（特别是非递归遍历）通常需要借助栈或者使用递归，这样会造成一定的空间和时间上的开销。线索二叉树通过利用空闲的指针字段，使得在遍历过程中能够直接找到节点的前驱和后继，从而避免了栈或递归的使用，减少了计算量和存储空间的需求。
将非线性的二叉树结构转化成线性结构的一种方式是通过遍历,如果使用链式存储二叉树的时候,我们往往只能通过遍历的手段获得某个节点的前驱和后继,这是因为使用链式存储二叉树的时候会发现节点有两个指针域,一个是指向左孩子,一个指向右孩子.
我们如何在非线性结构的二叉树中直接找到线性结构中的节点的前驱和后继节点的信息呢？
- 我们现在可以获取的关于遍历序列的线性结构的二叉树的关于节点的前驱和后继节点的信息只有根节点和叶子节点,即除根节点外每个节点都有且只有一个直接前驱节点,除叶子节点外的每个节点都有且只有一个后继节点,这是分析线性结构即遍历序列可以知道的信息)
那么我们如何通过在非线性结构的二叉树中直接找到线性结构中所有节点的直接前驱节点和后继节点呢 ?

在这里插入图片描述

种类

线索二叉树中的“线索”是根据二叉树的遍历顺序添加的，所以前序、中序和后序线索二叉树在相同的二叉树结构上会有不同的线索指向。

中序线索二叉树：

在这种类型的线索二叉树中，线索指向的是中序遍历的前驱和后继。也就是说，一个节点的左线索指向它的中序前驱，右线索指向它的中序后继。

前序线索二叉树：

在前序线索二叉树中，线索指向的是前序遍历的前驱和后继。因此，一个节点的左线索会指向它的前序前驱（如果存在），而右线索指向它的前序后继。

后序线索二叉树：

与前两者类似，后序线索二叉树中的线索指向的是后序遍历的前驱和后继。

由于前序、中序、后序遍历的访问顺序不同，因此即使是相同的二叉树，在不同类型的线索二叉树中，节点的线索指向确实是不同的。这也意味着，为同一个二叉树构建前序、中序或后序线索二叉树时，需要进行不同的处理逻辑，以确保线索正确地指向正确的前驱或后继节点。

我们在这里讲解的是 " 中序遍历二叉树的情况下给普通二叉树加入线索后构建中序线索二叉树 " !

示意图

1)未加入线索的普通二叉树示意图1.1

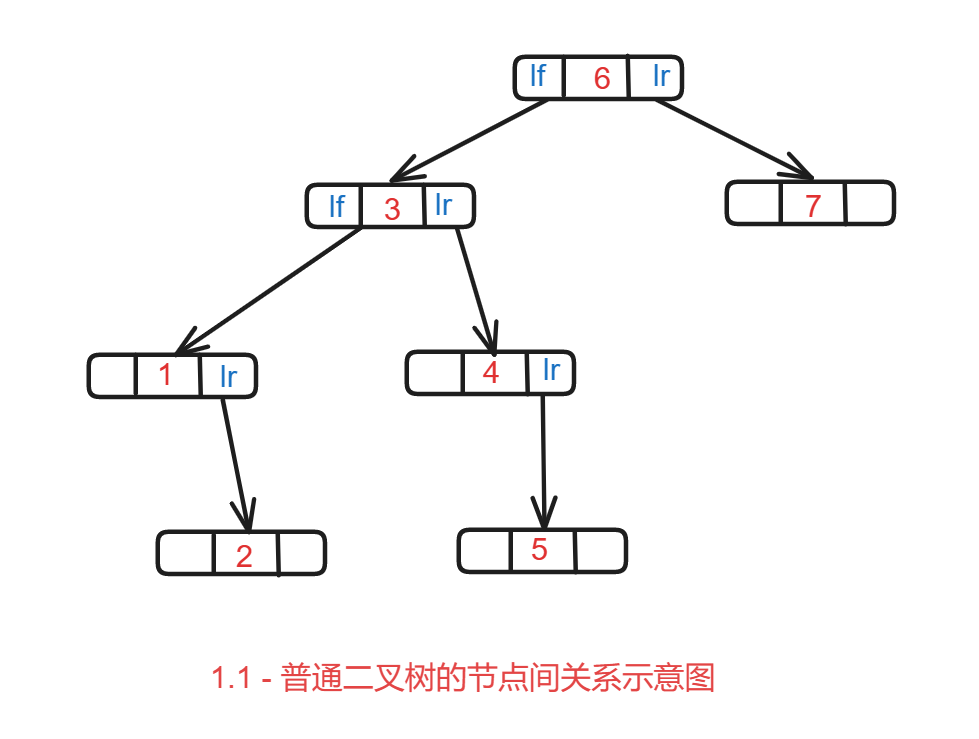
在这里插入图片描述

分析

上述的二叉树一共有n = 7 个节点,那么我们给这个二叉树的每个节点都添加了两个引用,那么我们可以知道二叉树中引用一共有 2n= 14 个, 有n-1 = 6 个引用是被占用了,那么就还剩下 2n - (n-1) = n + 1 = 8 个空闲的引用.
那么我们如果把这空闲出来的当做线索,也就是我们刚刚改造普通二叉树变成线索二叉树的讲解的方法二,我们就可以知道把这 8 个引用利用起来,分别指向当前节点的直接前驱节点或直接后继节点,这样就完成了线索的添加.

而且我们还可以利用线性结构的二叉树遍历结果知道 :
除第一个节点无直接前驱节点已经最后一个节点无直接后继节点外其余节点一定都有直接前驱节点和直接后继节点.所以 8 个引用中会有两个引用是空的,方别是第一个节点和最后一个节点.

<所以现在我们可以中序遍历给每个节点都添加上对应的前驱和后继节点>

2)线索添加的规则

对于每个节点:
- 如果节点的左指针为空，则将左指针指向其中序遍历的前驱节点，并标记左指针为线索。
- 如果节点的右指针为空，则将右指针指向其中序遍历的后继节点，并标记右指针为线索。
遍历过程:
- 从根节点开始，递归地对左子树进行中序遍历并线索化。
- 访问当前节点，设置线索。
- 递归地对右子树进行中序遍历并线索化。

3)中序线索二叉树示意图1.2

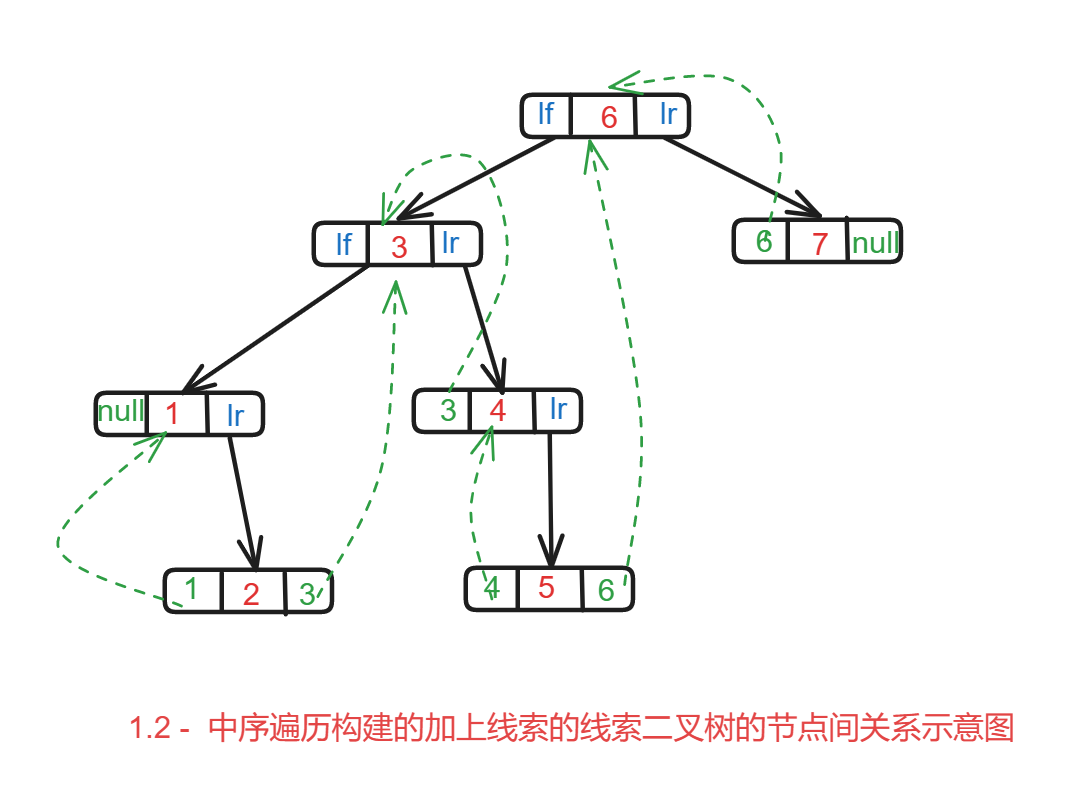
在这里插入图片描述

分析

的确,我们通过中序遍历这个二叉树的同时添加上线索之后,这个二叉树就叫做 线索二叉树

4)中序线索二叉树分析示意图1.3

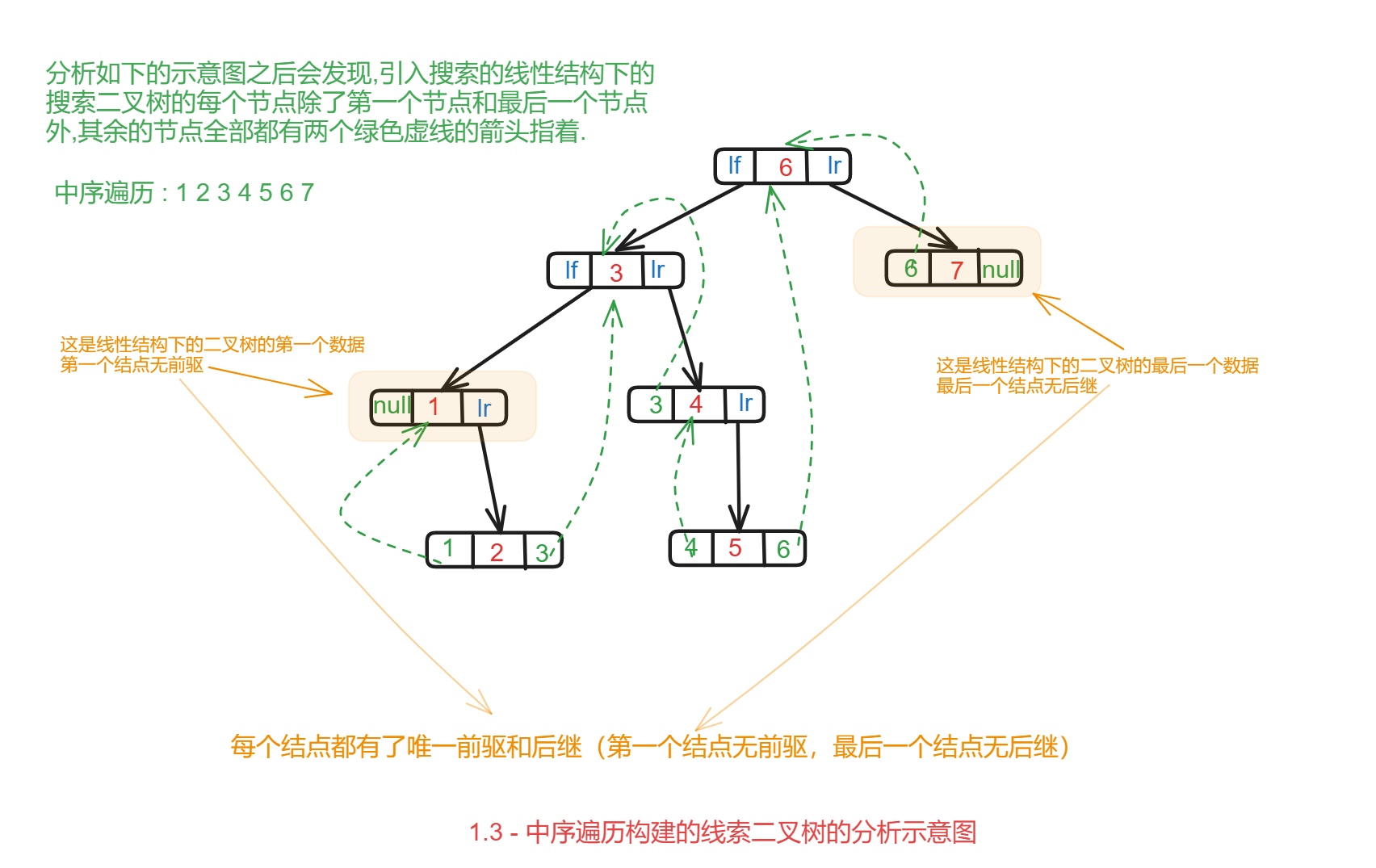
在这里插入图片描述

设计代码逻辑(重点)

我在这里先提前设计一下实现代码的思路,这样可以理清代码的逻辑.

代码的逻辑和实现框架概述：

类结构:
- ThreadedBinaryTree: 主类，用于实现线索二叉树。
- BinaryTreeNode: 嵌套静态类，表示二叉树的节点。
- DataIllegalException: 自定义异常类，用于处理非法数据。
主要属性:
- root: 二叉树的根节点。
- pre: 用于在线索化过程中保存前一个节点。
- size: 节点的数量。
构造方法:
- 无参构造器初始化线索二叉树。
- 带有根节点参数的构造器，用于创建带有根节点的线索二叉树。
核心方法:
- insertNode(): 向线索二叉树中插入新节点。
- inorderThreaded(): 对二叉树进行中序线索化。
- inThreadList(): 中序遍历线索化后的二叉树。
辅助方法:
- isEmpty(): 检查树是否为空。
- size(): 返回树的大小。
- getRoot(): 获取树的根节点。
- getLeft(), getRight(): 分别获取节点的左孩子和右孩子。
- checkParent(): 检查父节点是否为空。
- checkRootDataIllegal(): 检查节点数据是否非法。

代码实现

ThreadedBinaryTree类

package src.test.java;/*** 线索二叉树测试Threaded Binary Tree* 这个测试类目的是用来实现线索二叉树的(中序)*/
public class ThreadedBinaryTree<E> {private BinaryTreeNode<E> root = null;//根节点private BinaryTreeNode<E> pre = null; // 用于保存前一个节点private int size;//节点个数/***无参构造方法,可以完成部分属性的初始化*/public ThreadedBinaryTree(){}/**** @param root*/public ThreadedBinaryTree(BinaryTreeNode<E> root){try {checkRootDataIllegal(root.val);} catch (DataIllegalException e) {throw new RuntimeException(e);}this.root = root;size++;}/*** 判空* @return 如果二叉树为空则返回ture*/public boolean isEmpty(){return size==0;}/*** 检查数据是否为非法的数据* @param data val值* @throws DataIllegalException 自定义的异常(当数据为空的时候抛出该异常,并打印信息 "数据不能存储空值")*/private void checkRootDataIllegal(E data) throws DataIllegalException {if (data==null){throw new DataIllegalException("数据不能存储空值");}}/*** 节点个数* @return 返回的二叉树节点的个数*/public int size(){return size;}/*** 获取搜索二叉树的根节点* @return 根节点对象*/public BinaryTreeNode<E> getRoot(){return this.root;}/*** 获取左孩子* @param parent 父亲节点* @return 返回的当前父亲节点的左孩子*/public BinaryTreeNode<E> getLeft(BinaryTreeNode<E> parent){checkParent(parent);//注意需要判断传进来的父亲节点对象是否存在左孩子,如果存在才可以返回左孩子,如果不存在就返回nullreturn parent.left;}/*** 获取右孩子* @param parent 父亲节点* @return 返回当前父亲节点的右孩子*/public BinaryTreeNode<E> getRight(BinaryTreeNode<E> parent){//注意需要判断传进来的父亲节点是否存在右孩子,如果存在才可以返回右孩子对象,如果不存在就返回nullreturn parent.right;}/*** 检查父亲节点是否为空,如果为空的话就需要抛出异常* @param parent 传进来的父亲节点*/private void checkParent(BinaryTreeNode<E> parent){if(parent ==null){throw  new NullPointerException("父亲节点不能为空");}}/*** 向线索二叉树中插入节点* @param parent 父节点* @param child 要插入的新节点* @param isLeft 如果为true，则将节点插入为左孩子；如果为false，则为右孩子*/public void insertNode(BinaryTreeNode<E> parent, BinaryTreeNode<E> child, boolean isLeft) {if (parent == null) {if (root == null) {root = child; // 如果根节点为空，则新节点成为根节点} else {throw new IllegalStateException("不能在空的父节点上插入");}} else {if (isLeft && parent.left == null) {parent.left = child;} else if (!isLeft && parent.right == null) {parent.right = child;} else {throw new IllegalStateException("指定的位置已有节点");}}size++;}// 线索遍历函数// 实现中序遍历的同时线索化public void inorderThreaded() {inorderThreaded(this.root);}private void inorderThreaded(BinaryTreeNode<E> node) {if (node == null) {return;}// 遍历左子树inorderThreaded(node.left);// 处理当前节点的前驱if (node.left == null) {node.left = pre;node.isLeftThread = true;}// 处理前一个节点的后继if (pre != null && pre.right == null) {pre.right = node;pre.isRightThread = true;}pre = node; // 更新前一个节点// 遍历右子树inorderThreaded(node.right);}/*** 中序遍历线索二叉树*/public void inThreadList(BinaryTreeNode<E> root) {if (root == null) {return;}//查找中序遍历的起始节点while (root != null && !root.isLeftThread) {root = root.left;}while (root != null) {System.out.print(root.val + " ");// 如果右子节点是线索if (root.isRightThread) {root = root.right;} else {//有右子节点，遍历右子节点root = root.right;//如果右子节点不为null，并且右子节点的左子结点存在while (root != null && !root.isLeftThread) {root = root.left;}}}}/*** 封装的节点类* @param <E>*/static   class BinaryTreeNode<E> {//数据域public E val;//保存左孩子或者直接前驱节点的引用(保存直接前驱节点的条件是没有左孩子,如果有左孩子就直接指向左孩子)public BinaryTreeNode<E> left;//保存右孩子或者直接后继节点的引用(保存直接后继节点的条件是没有右孩子,如果有右孩子就直接指向右孩子)public BinaryTreeNode<E> right;public boolean isLeftThread;  // 左指针是否为线索public boolean isRightThread; // 右指针是否为线索/*** 构造方法** @param val 创建节点的时候就初始化data的数值*/public BinaryTreeNode(E val) {this.val = val;this.left = null;this.right = null;this.isLeftThread = false;this.isRightThread = false;}/*** 重写ToString()方法** @return*/public String toString() {return this.val.toString();}}}class DataIllegalException extends Exception{public DataIllegalException(String m){super(m);}
}

Test测试类

package src.test.java;public class ThreadedBinaryTreeTest {public static void main(String[] args) {ThreadedBinaryTree<Integer> tree = new ThreadedBinaryTree<>();// 创建节点ThreadedBinaryTree.BinaryTreeNode<Integer> node6 = new ThreadedBinaryTree.BinaryTreeNode<>(6);//添加r根节点的左子结点node3ThreadedBinaryTree.BinaryTreeNode<Integer> node3 = new ThreadedBinaryTree.BinaryTreeNode<>(3);//添加r根节点的右子结点node7ThreadedBinaryTree.BinaryTreeNode<Integer> node7 = new ThreadedBinaryTree.BinaryTreeNode<>(7);//添加a节点的左子结点node1ThreadedBinaryTree.BinaryTreeNode<Integer> node1 = new ThreadedBinaryTree.BinaryTreeNode<>(1);//添加a节点的右子结点node4ThreadedBinaryTree.BinaryTreeNode<Integer> node4 = new ThreadedBinaryTree.BinaryTreeNode<>(4);//添加b节点的右子结点node2ThreadedBinaryTree.BinaryTreeNode<Integer> node2 = new ThreadedBinaryTree.BinaryTreeNode<>(2);//添加c节点的左子结点node5ThreadedBinaryTree.BinaryTreeNode<Integer> node5 = new ThreadedBinaryTree.BinaryTreeNode<>(5);// 插入节点tree.insertNode(null, node6, true);tree.insertNode(node6, node3,true);tree.insertNode(node6, node7, false);tree.insertNode(node3, node1, true);tree.insertNode(node3, node4, false);tree.insertNode(node1, null,true);tree.insertNode(node1, node2,false);tree.insertNode(node4, null, true);tree.insertNode(node4, node5, false);tree.insertNode(node2, null, false);tree.insertNode(node2, null, true);tree.insertNode(node5, null, true);tree.insertNode(node5, null, false);tree.insertNode(node7, null, true);// 线索化tree.inorderThreaded();//遍历二叉树tree.inThreadList(tree.getRoot());}
}