多元函数奇偶性
多元函数的定义域
- 定义域根据函数的变量数不同,有不同的形式
- 一元函数 y = f ( x ) y=f(x) y=f(x),定义域可以是数集
- 二元函数 z = f ( x , y ) z=f(x,y) z=f(x,y),定义域可以是一平面区域,是平面点集
- 三元函数 v = f ( x , y , z ) v=f(x,y,z) v=f(x,y,z),定义域是一块空间区域,是空间点集
- …
- n n n圆函数,定义域为 n n n维点集
自然定义域
- 根据仅根据表达式本身是否有意义来判定定义域
- 比如分式中分母不为0
- 偶次根式内不可为负数
- 对数函数的真数为正数
特定定义域
- 根据实际需要或者认为规定的的区域,比如给定积分区域(积分限)
n n n元函数
-
y y y是一个 n n n元函数,记为 y = f ( x 1 , x 2 , ⋯ , x i , ⋯ , x n ) y=f(x_1,x_2,\cdots,x_i,\cdots,x_n) y=f(x1,x2,⋯,xi,⋯,xn)
- 其中 x i x_i xi表示函数 f f f的第 i i i个自变量
奇偶性
- 一般讨论的是关于某个自变量 x i x_i xi的奇偶性
- 设 n n n元函数 y = f ( x 1 , x 2 , ⋯ , x i , ⋯ , x n ) y=f(x_1,x_2,\cdots,x_i,\cdots,x_n) y=f(x1,x2,⋯,xi,⋯,xn), f f f是关于 x i x_i xi的偶函数,则 f ( x 1 , x 2 , ⋯ , − x i ‾ , ⋯ , x n ) f(x_1,x_2,\cdots,\large\underline{-x_i}\normalsize,\cdots,x_n) f(x1,x2,⋯,−xi,⋯,xn)= f ( x 1 , x 2 , ⋯ , x i ‾ , ⋯ , x n ) f(x_1,x_2,\cdots,\large\underline{x_i}\normalsize,\cdots,x_n) f(x1,x2,⋯,xi,⋯,xn)
- 若 f f f是关于 x i x_i xi的奇函数 f ( x 1 , x 2 , ⋯ , − x i ‾ , ⋯ , x n ) f(x_1,x_2,\cdots,\large\underline{-x_i}\normalsize,\cdots,x_n) f(x1,x2,⋯,−xi,⋯,xn)= − f ( x 1 , x 2 , ⋯ , x i ‾ , ⋯ , x n ) \large-\normalsize f(x_1,x_2,\cdots,\large\underline{x_i}\normalsize,\cdots,x_n) −f(x1,x2,⋯,xi,⋯,xn)
一元函数
- y = f ( x ) y=f(x) y=f(x)
- 若 f ( x ) f(x) f(x)为偶函数: f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x)关于 x = 0 x=0 x=0( y y y轴)对称
- 若 f ( x ) f(x) f(x)维奇函数: f ( − x ) = − f ( x ) f(-x)=-f(x) f(−x)=−f(x),关于 ( 0 , 0 ) (0,0) (0,0)(原点)对称
二元函数
-
z = f ( x , y ) z=f(x,y) z=f(x,y)
-
以分量 x x x为例
- 奇函数: f ( − x , y ) = − f ( x , y ) f(-x,y)=-f(x,y) f(−x,y)=−f(x,y),函数关于点 ( 0 , y , 0 ) (0,y,0) (0,y,0)对称
- 设 P ( x , y , z ) P(x,y,z) P(x,y,z)是 f ( x , y ) f(x,y) f(x,y)上的点, z = f ( x , y ) z=f(x,y) z=f(x,y),而 f ( − x , y ) f(-x,y) f(−x,y)= − f ( x , y ) -f(x,y) −f(x,y)= − z -z −z
- 则 Q ( − x , y , − z ) Q(-x,y,-z) Q(−x,y,−z)也位于 f ( x , y ) f(x,y) f(x,y)上
- P , Q P,Q P,Q两点的位置关系?
- 方法1:
- 显然两个点有相同的 y y y轴坐标,从而它们必然同时位于平面 y = y y=y y=y上
- 并且两个点有互为相反数的 x , y x,y x,y轴坐标, P P P位于平面 x = x , z = z x=x,z=z x=x,z=z两平面交线上,而 Q Q Q位于 x = − x , y = − y x=-x,y=-y x=−x,y=−y两平面的交线上,这两条交线关于原点(或 y y y轴)对称,分别和平面 y = y y=y y=y所截,得到 P , Q P,Q P,Q两点
- 因此 P , Q P,Q P,Q两点关于 ( 0 , y , 0 ) (0,y,0) (0,y,0)对称
- 方法2:
- 由两点间坐标公式, ( − x + x 2 , y + y 2 , z − z 2 ) (\frac{-x+x}{2},\frac{y+y}{2},\frac{z-z}{2}) (2−x+x,2y+y,2z−z)= ( 0 , y , 0 ) (0,y,0) (0,y,0),可知 P , Q P,Q P,Q两点关于 M ( 0 , y , 0 ) M(0,y,0) M(0,y,0)对称
- M M M点位于直线 x = 0 , z = 0 x=0,z=0 x=0,z=0上(即 y y y轴上)
- 因此 P , Q P,Q P,Q两点关于 ( 0 , y , 0 ) (0,y,0) (0,y,0)对称
- 方法1:
- 因此,函数 f ( x , y ) f(x,y) f(x,y)的图形关于 y y y轴对称
- 偶函数: f ( − x , y ) = f ( x , y ) f(-x,y)=f(x,y) f(−x,y)=f(x,y),函数关于平面 x = 0 x=0 x=0对称
- 设 P ( x , y , z ) P(x,y,z) P(x,y,z)是 f ( x , y ) f(x,y) f(x,y)上的点, z = f ( x , y ) z=f(x,y) z=f(x,y),而 f ( − x , y ) f(-x,y) f(−x,y)= f ( x , y ) f(x,y) f(x,y)= z z z
- 则 Q ( − x , y , z ) Q(-x,y,z) Q(−x,y,z)也位于 f ( x , y ) f(x,y) f(x,y)上
- 由中点坐标公式: P , Q P,Q P,Q的中点为 ( 0 , y , z ) (0,y,z) (0,y,z),该点属于平面 x = 0 x=0 x=0
- P , Q P,Q P,Q两点关于 x = 0 x=0 x=0(即坐标面 y O z yOz yOz面)对称
- 因此函数 f ( x , y ) f(x,y) f(x,y)的图形关于 x = 0 x=0 x=0面对称
- 奇函数: f ( − x , y ) = − f ( x , y ) f(-x,y)=-f(x,y) f(−x,y)=−f(x,y),函数关于点 ( 0 , y , 0 ) (0,y,0) (0,y,0)对称
-
分量 y y y类似地讨论
-
小结
- 在一元函数 y = f ( x ) y=f(x) y=f(x)中,偶函数是关于直线 ( x = 0 ) (x=0) (x=0)对称,而奇函数关于点 ( 0 , 0 ) (0,0) (0,0),即 x = 0 , y = 0 x=0,y=0 x=0,y=0对称
- 点表示为 ( x , y ) (x,y) (x,y)
- 在二元函数 z = f ( x , y ) z=f(x,y) z=f(x,y)中,偶函数是关于面对称,而奇函数关于直线对称
- 点表示为 ( x , y , z ) (x,y,z) (x,y,z)
- 以自变量 x x x为例,关于 x x x的偶函数图形关于 x = 0 x=0 x=0面对称,奇函数图形关于 x = 0 , z = 0 x=0,z=0 x=0,z=0,即 y y y轴
- 而对于自变量 y y y,关于 y y y的偶函数图形关于 y = 0 y=0 y=0面对称,奇函数图形关于 y = 0 , z = 0 y=0,z=0 y=0,z=0,即 y y y轴
- 也就是说,对称中心都上升了一个维度,从点到线,从线到面
- 本质上都是两点关于它们的中点对称,分析中点的特点来判断对称中心是什么
结论分析和记忆👺
- 对于一元奇(偶)函数为,自变量轴为 x x x轴
- 自变量 x x x沿着从原点(或正区间内第一点有定义的 x 0 x_0 x0处)开始,分析曲线变化
- 若 f ( x ) f(x) f(x)是奇函数, x x x向 x x x轴正方向进行的变化情况与负方向的变化情况相反
- 若 f ( x ) f(x) f(x)是偶函数, x x x向 x x x轴正方向进行的变化情况与负方向的变化情况相同(对称)
- 对于二元奇(偶)函数,自变量设为 x , y x,y x,y,分析曲面的变化情况
- 若 f ( x , y ) f(x,y) f(x,y)是关于 x x x的奇函数, x x x向 x x x轴正方向进行的变换情况与负方向的变化情况相反
- 若 f ( x , y ) f(x,y) f(x,y)是关于 x x x偶函数, x x x向 x x x轴正方向进行的变化情况与负方向的变化情况相同(对称)
推广
- 更一般的
- 对于 n n n元函数 w = f ( x 1 , x 2 , ⋯ , x n ) w=f(x_1,x_2,\cdots,x_n) w=f(x1,x2,⋯,xn),视为 n + 1 n+1 n+1维空间,将写维点的形式: ( x 1 , x 2 , ⋯ , x n , w ) (x_1,x_2,\cdots,x_n,w) (x1,x2,⋯,xn,w)
- 若 f f f关于自变量 x i x_i xi为奇函数(以 i = 1 i=1 i=1为例),那么 P ( x 1 , x 2 , ⋯ , x n , w ) P(x_1,x_2,\cdots,x_n,w) P(x1,x2,⋯,xn,w), Q ( − x 1 , x 2 , ⋯ , x n , − w ) Q(-x_1,x_2,\cdots,x_n,-w) Q(−x1,x2,⋯,xn,−w),其对称中心点为 M ( 0 , x 2 , ⋯ , x n , 0 ) M(0,x_2,\cdots,x_n,0) M(0,x2,⋯,xn,0),对称中心为超平面 x 1 = 0 , w = 0 x_1=0,w=0 x1=0,w=0;(即令第 i i i维自变量取0和最后意味取 0 0 0)
- 若 f f f关于自变量 x i x_i xi为偶函数(以 i = 1 i=1 i=1为例),那么 P ( x 1 , x 2 , ⋯ , x n , w ) P(x_1,x_2,\cdots,x_n,w) P(x1,x2,⋯,xn,w), Q ( − x 1 , x 2 , ⋯ , x n , w ) Q(-x_1,x_2,\cdots,x_n,w) Q(−x1,x2,⋯,xn,w),其对称中心点为 M ( 0 , x 2 , ⋯ , x n , w ) M(0,x_2,\cdots,x_n,w) M(0,x2,⋯,xn,w),对称中心为超平面 x 1 = 0 x_1=0 x1=0
- 当 i ≠ 1 i\neq{1} i=1时,情形类似
应用和实例
例
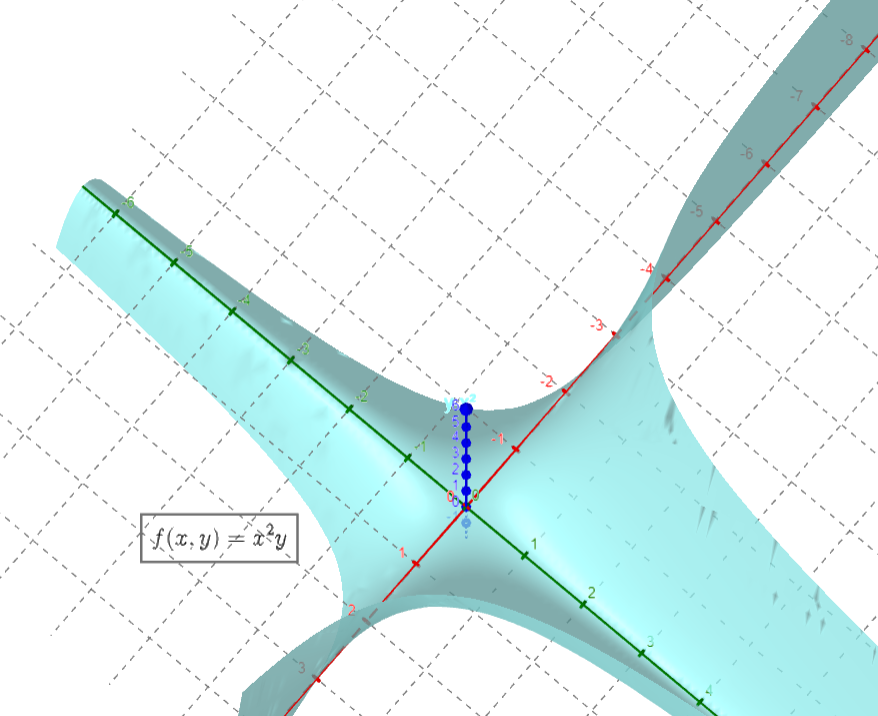
- f ( x , y ) f(x,y) f(x,y)= y x 2 y{x^2} yx2,假设 f f f的定义域(区域)是关于 x , y x,y x,y轴对称的区域(比如其自然定义域下)
- 那么显然, f f f关于 y y y是奇函数;图形关于 x x x轴对称
- 同时 f f f是关于 x x x的偶函数,图形关于 x = 0 x=0 x=0平面对称
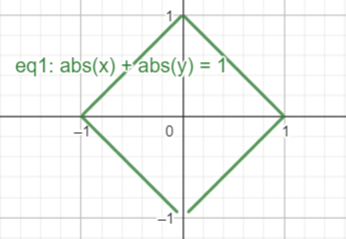
二元绝对值不等式确定的区域
-
∬ D ( ∣ x ∣ + y e x 2 ) d σ \iint\limits_{D}({|x|+ye^{x^2}})\mathrm{d}\sigma D∬(∣x∣+yex2)dσ, ( D : ∣ x ∣ + ∣ y ∣ = 1 ) (D:|x|+|y|=1) (D:∣x∣+∣y∣=1)
-
二元一次绝对值方程对应的草图
-
对于 g ( x , y ) = ∣ x ∣ + ∣ y ∣ = 1 g(x,y)=|x|+|y|=1 g(x,y)=∣x∣+∣y∣=1,前去绝对值
- ∣ x ∣ = x |x|=x ∣x∣=x, ( x ⩾ 0 ) (x\geqslant{0}) (x⩾0); ∣ x ∣ = − x |x|=-x ∣x∣=−x, ( x < 0 ) (x<0) (x<0)
- ∣ y ∣ = y |y|=y ∣y∣=y, ( y ⩾ 0 ) (y\geqslant{0}) (y⩾0), ∣ y ∣ = − y |y|=-y ∣y∣=−y, ( y < 0 ) (y<0) (y<0)
-
得到四个二元一次方程:在平面直角坐标系 x O y xOy xOy中对应于4条直线段
- 1 = { − x − y , x < 0 , y < 0 − x + y x < 0 , y ⩾ 0 x − y , x ⩾ 0 , y < 0 x + y , x ⩾ 0 , y ⩾ 0 1=\begin{cases} -x-y,&x<0,y<0 \\-x+y &x<0,y\geqslant 0 \\x-y,&x\geqslant 0,y<0 \\x+y,&x\geqslant 0,y\geqslant 0 \end{cases} 1=⎩ ⎨ ⎧−x−y,−x+yx−y,x+y,x<0,y<0x<0,y⩾0x⩾0,y<0x⩾0,y⩾0
-
四条直线段所在直线分别转换为斜截式: y = − x − 1 y=-x-1 y=−x−1; y = x + 1 y=x+1 y=x+1; y = − x − 1 y=-x-1 y=−x−1; y = 1 − x y=1-x y=1−x
-
-
将他们分别绘制,得到一个边长为1的正方形(菱形)