汉诺塔问题：

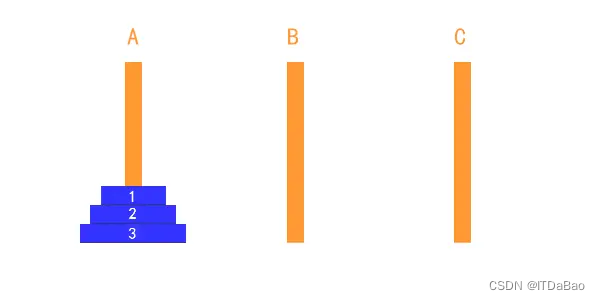
​ 给定三根柱子，记为 ，其中A,B,C 柱子上有 n个盘子，从上到下编号为
0到n-1, ，且上面的盘子一定比下面的盘子小。问：将A柱上的盘子经由B柱移动到C柱最少需要多少次？

思路分析：
把所有的盘子分成两个部分，除了最下面的盘子，其他的盘子视为一个整体。

（1）上面的所有盘子从开始位置移动到中间位置
（2）最下面的盘子直接从开始位置移动到目标位置
（3）上面的所有盘子从中间位置移动到目标位置。

public class D4_Hannuota {public static void main(String[] args) {hanoi(2,'a','b','c');}/*n:N个盘子from:开始in:中间to：目标无论多少盘子，都认为只有两个，上面的和最后一个。*/public static void hanoi(int n,char from,char in,char to) {if(n==1){System.out.println("第"+n+"个盘子从:"+from+"移动到："+to);}else {//移动上面的所有盘子到中间位置hanoi(n-1,from,to,in);//移动下面盘子从开始位置到目标位置System.out.println("第"+n+"个盘子从:"+from+"移动到："+to);//上面的盘子从中间位置到目标位置hanoi(n-1,in,from,to);}}
}