深度模型压缩研究回顾
作者:安静到无声 个人主页
目录
- 深度模型压缩研究回顾
- 推荐专栏
在本节中,主要介绍了目前主流的深度神经网络压缩与加速方法,主要包括轻量化网络设计、参数量化、知识蒸馏、模型剪枝和硬件加速等,其中模型剪枝与硬件加速与本文研究最为相关。
3.1 轻量化网络设计研究现状
紧凑的神经网络设计方法并未对预先训练网络模型进行压缩,而是直接设计出具有较小计算复杂度和参数量的新型网络。SqueezeNet[1]利用1×1卷积和分组卷积,在AlexNet[2]上实现了约50倍的压缩,并且具有相当的精度。SqueezeNext[3]基于SqueezeNet改进了网络结构,并从硬件角度分析如何提速。MobileNetV1[4]利用深度可分离卷积模块构建的轻量化模型取得了不错的结果,如图1所示。MobileNetV2[5]在MobileNetV1的基础上,借鉴ResNet的残差结构,提出基于反向残差的线性瓶颈结构,实现了惊人识别效果。ShuffleNet[6]利用分组卷积和通道混洗的方法来减少模型的参数量和计算量,进而提升推理速度,ShuffleNetV2[7]指出FLOPs不能直接线性的衡量计算速度,速度与硬件设备也有关联,因此在此基础上改进了ShuffleNetV1网络结构[8]。
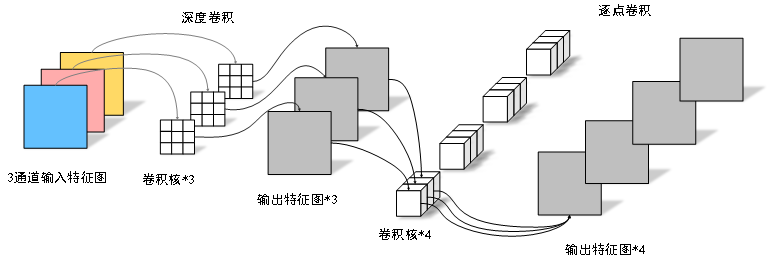
图1 Mobilenet中的深度可分离卷积计算示意图
除了上述网络结构轻量化的方法之外,还有一些研究围绕着构造轻量化的卷积块展开。Pravendrad等人[9]设计了一种高效的异核卷积滤波器(HetConv),插入任何现有的架构中,可以提高架构的效率(FLOPs减少3至8倍),而且不会牺牲精度,如图2所示。OctConv[10]将特征图分为高频特征图和低频特征图,并通过降低低频特征图的分辨率而节省存储和计算量,同时有助于获得更大的感受野。Liu等人[11]在分组卷积的基础上提出了捆绑块卷积(Tied Block Convolution, TBC)它在相同大小的通道块上共享相同thinner的滤波器,并用一个滤波器产生多个响应,实现了模型的轻量化设计。DualConv[12]结合3×3和1×1卷积核来同时处理相同的输入特征映射通道,并利用组卷积技术来有效地排列滤波器,解决了跨通道通信和保持原始输入特征图信息的问题。
图2 异核卷积结构示意图
虽然这些轻量级的网络已经取得了很好的检测性能,但是这种手工设计的成本很高,并且随着网络的复杂而变得困难。此外,利用网络架构搜索的方法进行轻量化网络设计也变得很流行。姚潇等人[13]利用不同分组的ShffleNet单元和Dilated LightNet单元作为搜索空间,利用ENAS网络[14]搜索架构确定网络的分组结构和整体架构。但是这些方法的搜索空间非常大,需要消耗大量的计算资源。
3.2 参数量化技术研究现状
神经网络参数量化(Quantization)通过降低模型比特数以及优化比特运算的方法对初始神经网络模型进行压缩,使模型更易于数字硬件实现[15]。根据量化是否需要重新训练或微调划分为量化感知训练(Quantization-Aware Training,QAT)和后量化(Post-Training Quantization,PTQ)方法。
(1)量化感知训练。
该方法首先对预训练模型进行量化,然后使用训练数据进行微调,最后调整参数以恢复下降的精度。Zhuang等人[16]使用一个两阶段优化策略解决低精度网络容易陷入较差局部最小值的问题,并提出一种联合学习模型以充分学习全精度模型提取的特征信息。Angela Fan等人[17]提出量化噪声技术来训练出高性能的量化网络。除了调整模型参数外,以前的一些工作也发现在量化感知训练方法中,在测试过程中学习量化参数也是有效的。Jungwook[18]利用一种新颖的激活量化方案来学习最优量化尺度。Jung等人[19]将量化区间参数化,通过最小化网络的任务损失来获得最优值。LSQ[19]引入一种新的梯度估计方法来学习非负性激活的比例因子。LSQ+[41]进一步将这一想法扩展到一般的激活函数,如S-wish和H-swish这些会产生负值函数。尽管在这个领域有如此多有意义的工作,可是这种方法存在计算开销大、压缩尺寸有限等问题,难以实现快速有效的部署。
(2)训练后量化。
在训练后量化中,使用校准数据(例如,训练数据的小子集)来校准预训练模型,以计算尺度因子和比例因子,然后,基于校准结果量化该模型,以此提升了深度神经网络实际部署效率。如,Banner等人[22]设计了一种基于阶段阈值选择方案的量化方法,通过分析计算截断范围以及每个通道的比特数分配实现相对较好的测试性能。然而,由于使用多通道来量化激活值,使得难以部署在硬件平台上。Fang等人[23]提出了一种分段线性量化方案,以实现对具有长尾钟形分布的张量值的精确逼近。该方法将每个张量的量化范围划分为不重叠的区域,然后为每个区域分配相同数量的量化级别,并通过最小化量化误差来确定划分整个范围的最佳断点。Choukroun等人[24]将线性量化任务转换为权重和激活值的最小均方差(MMSE)问题,避免了对模型的重新训练。因此,PTQ是一种非常快速的量化神经网络模型的方法。然而,与QAT相比,这往往以较低的准确性为代价。
3.3 知识蒸馏技术研究现状
知识蒸馏是一种训练框架,一般流程如图3所示。其原理是将大的预训练教师模型的特征信息转移到一个小型学生模型中,并保证在资源有限的学生模型中保持教师的准确性[25]。尽管在工程实践中该技术取得了巨大的成功,但是从理论解释上来理解知识蒸馏研究并不多。Phuong和Lampert[26]通过研究深层线性分类器证明了一个泛化界限,该界限建立了蒸馏训练线性分类器的预期风险的快速收敛。也说明了知识蒸馏的成功依赖于数据几何、蒸馏目标的优化偏差和学生分类器的强单调性。Ji等人[27]从风险界限、数据效率和教师模型不完善的角度理论上解释了宽神经网络上的知识蒸馏。Cho和Hariharan[28]实证分析了知识蒸馏的效果,结果表明,由于模型容量差距,大模型可能不是更好的老师。Cheng等人[29]通过量化和分析深度神经网络中间层中与任务相关和与任务无关的视觉概念来以解释知识蒸馏。
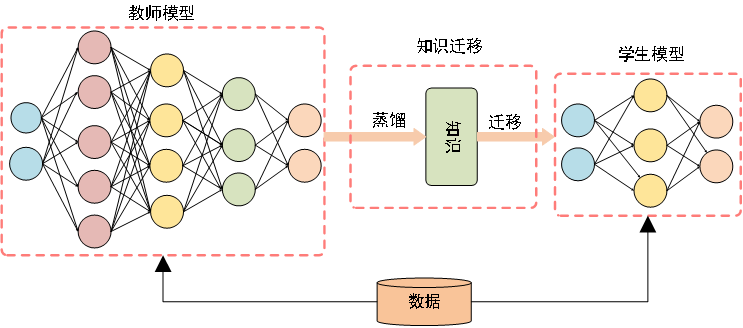
图3 知识蒸馏的通用师生框架
知识蒸馏方法已扩展到师生学习、相互学习、终身学习和自学。不过大多数知识蒸馏的扩展都集中在压缩深度神经网络上,由此产生的轻量级学生网络可以轻松部署到无人机、移动手机和机器人等设备中。FitNets[30]利用教师的中间表征直接指导学生模型中的学习中间表征,扩展了知识提炼。Shen等人[31]提出了一种知识蒸馏的新范式MEAL,将多个训练的深度神经网络的知识转移到单个深度神经网络。为了从不同的训练(教师)模型中提取不同的知识,采用了对抗学习策略以指导和优化预定义的学生网络来恢复教师模型中的知识,并促使判别器网络同时区分教师和学生模型特征。
近两年也有不少知识蒸馏的研究成果。Mirzadeh等人[32]观察到,当教师和学生之间存在较大的能力差距时(即模型的复杂性差异很大),知识蒸馏可能会导致学生准确性下降。为了缩小能力差距,他们引入了教师助理的概念,提高了学习能力。Xu等人[33]利用具有选择性传递的噪声自监督信号进行蒸馏。尽管这些训练方法可以提高模型的识别效果,但是如何设计一个轻量高效的学生模型仍是一个亟待攻克的难题。
3.4 模型剪枝技术研究现状
剪枝是模型压缩中非常有效的方式,按照剪枝的稀疏度可以分为非结构化剪枝和结构化剪枝,图4展示了卷积神经网络4维权重张量的不同稀疏结构,其中规则稀疏使得硬件加速变得容易。
(1)非结构化剪枝
非结构化剪枝通过去除滤波器中的单个神经元或在全连接层中贡献较小的连接来降低CNN的计算成本。LeCun等人[34]提出了OBD(Optical Brain Damage, OBD)算法是非结构剪枝最为经典的文章,它利用二阶导数来平衡训练损失和模型复杂度。Suraj Srinivas[35]提出了一种无数据的方法对全连接层进行修剪,从而得到一个同等性能的紧凑子网络。Han等人[36]根据神经元连接权值的范数值大小,删除范数小于阈值的连接,并通过重新训练恢复性能。Liu等人[37]利用二维DCT变换对系数进行稀疏化,去除空间冗余。Dong等人[38]提出了一种叫做L-OBS的剪枝算法,该算法利用分层误差函数的二阶导数信息对参数进行剪枝,使模型在性能下降很小的情况下修剪大量参数。Chen[39]等人从约束贝叶斯优化的角度阐述了模型压缩问题,并引入一种冷却(退火)策略进行求解。Lin等人[40]提出了一种动态分配稀疏模式和包含反馈信号的方法来重新激活早期修剪的权值。尽管在权重参数层面做细粒度的剪枝,灵活性大精度高,但需要配合专门做稀疏矩阵运算的软硬件才能达到实用效果。
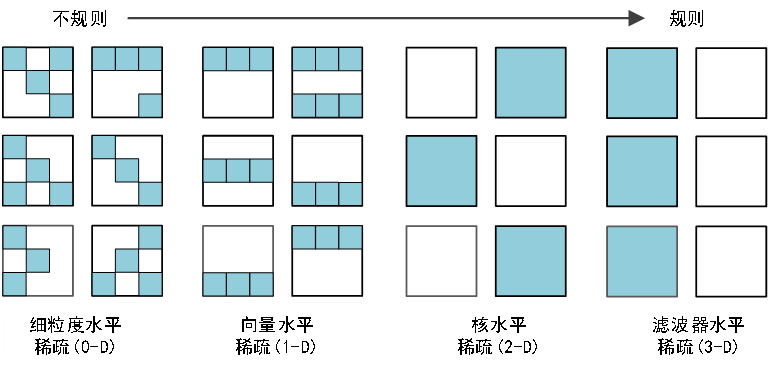
图12 卷积神经网络四维权重张量的不同稀疏结构
(2) 结构化剪枝
相比之下,结构化修剪可以直接移除通道和相应的滤波器,是一种硬件友好的神经网络修剪方法,因此可以容易地部署在嵌入式设备上。根据模型压缩的操作过程,结构化剪枝可以大致分为三类:预训练-属性剪枝、正则化-再训练剪枝和自动子网搜索。
预训练-属性剪枝:这种剪枝通常提出一个滤波器重要性的度量标准进行模型压缩。Li等人[41]使用L1范数对特征信息量少的滤波器进行修剪,并对重要的权重进行继承。NISP[42]应用特征排序技术(Final Response Layer, FRL)来度量每个神经元的重要性,进而将网络剪枝问题描述为一个二进制整数优化问题。He等人[43]分析了基于范数的网络修剪的局限性,并提出一种基于几何中值的滤波器修剪策略。Lin等人[44]利用特征图秩来评价滤波器的重要程度,保留了高秩特征图对应的滤波器权值。Hu等人[45]认为输出稀疏的通道是冗余的,因此去掉了相应的滤波器,并使用基于激活层中零的百分比的平均百分比(Average Percentage of Zeros, APoZ)作为度量。有研究考虑参数剪枝对损失的影响,Lee等人[46]直接利用导数对随机初始化的权重进行非结构化剪枝。这些方法的模型评估函数需要特别设计的,它们具有时间复杂度低的优点,但在性能和剪枝结果压缩率方面存在局限性。
正则化-再训练剪枝。与基于神经网络固有属性的方法不同,该方法在训练过程中引入稀疏约束和掩码方案来降低模型复杂度。例如,Wen等人[47]提出了一种结构化稀疏学习(Structured Sparsity Learning, SSL)方法来正则化DNN的结构(滤波器、通道、滤波器形状和层深度),进而获得硬件友好的结构稀疏性。Liu等人[48]和Zhao等人[49]对批归一层的尺度因子施加稀疏约束,并认为尺度因子较低的通道不重要。Huang等人[50]和Lin等人[51]引入了一个掩码来学习稀疏结构剪枝,去掉了比例因子为零对应的滤波器。Lemaireet等人[52]提出了一种结合预算约束稀疏性损失的知识蒸馏损失函数来训练网络,同时保证神经元预算。将剪枝要求嵌入到网络训练损失中,通过联合再训练优化生成自适应剪枝决策,通常可以获得更好的压缩和加速效果。但通常需要从头开始训练,在机器时间和人力上都是繁重的。此外,由于稀疏约束的引入,给训练损失的普适性和灵活性带来了很大的困难。
自动子网络搜索。最近的一些研究[53][54]侧重于寻找最佳网络结构,即每层通道的数,而不是评估滤波器的重要性。MetaPrunning[55]将每一层的输出通道数随机采样作为输入,训练修剪网络为不同架构的子网络模型生成的高质量权重,最后使用进化算法搜索满足约束的最优子网络。AMC[56]将压缩率和准确度作为反馈,使用强化学习获得智能体,生成每层的修剪率。然而,强化学习通常存在不稳定的收敛性,这需要进行大量的超参数调整。ABCPruner[57]使用人工蜂群算法自动搜索高效的网络架构,并对其进行微调,以选择最高效的子网络,但它需要重新训练子网络模型以进行性能评估,这会导致较高的计算成本。DMCP[58]将通道修剪建模为可微马尔可夫过程,从而消除了搜索许多体系结构的负担。然而,这些方法具有复杂的过程,需要迭代搜索,这将面临较高的计算成本,并可能导致次优搜索结果。
四、参考文献
[1] Iandola F N, Han S, Moskewicz M W, et al. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and< 0.5 MB model size[J]. arXiv preprint arXiv:1602.07360, 2016.
[2] Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[J]. Advances in neural information processing systems, 2012, 25.
[3] Gholami A, Kwon K, Wu B, et al. Squeezenext: Hardware-aware neural network design[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. Salt Lake City: IEEE, 2018: 1638-1647.
[4] Howard A G, Zhu M, Chen B, et al. Mobilenets: Efficient convolutional neural networks for mobile vision applications[J]. arXiv preprint arXiv:1704.04861, 2017.
[5] Sandler M, Howard A, Zhu M, et al. Mobilenetv2: Inverted residuals and linear bottlenecks[C]. Proceedings of the IEEE conference on computer vision and pattern recognition. Salt Lake City: IEEE, 2018: 4510-4520.
[6] Zhang X, Zhou X, Lin M, et al. Shufflenet: An extremely efficient convolutional neural network for mobile devices[C]. Proceedings of the IEEE conference on computer vision and pattern recognition. Salt Lake City: IEEE, 2018: 6848-6856.
[7] Ma N, Zhang X, Zheng H T, et al. Shufflenet v2: Practical guidelines for efficient cnn architecture design[C]. Proceedings of the European conference on computer vision. Munich: Springer, 2018: 116-131.
[8] 毕鹏程, 罗健欣, 陈卫卫. 轻量化卷积神经网络技术研究[J]. 计算机工程与应用, 2019,55(16):25-35. DOI:10.3778/j.issn.1002-8331.1903-0340.
[9] Singh P, Verma V K, Rai P, et al. Hetconv: Heterogeneous kernel-based convolutions for deep cnns[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 4835-4844.
[10] Chen Y, Fan H, Xu B, et al. Drop an octave: Reducing spatial redundancy in convolutional neural networks with octave convolution[C]. Proceedings of the IEEE/CVF International Conference on Computer Vision. Long Beach: IEEE, 2019: 3435-3444.
[11] Wang X, Stella X Y. Tied block convolution: leaner and better cnns with shared thinner filters[J]. arXiv preprint arXiv:2009.12021, 2020, 5.
[12] Zhong J, Chen J, Mian A. DualConv: Dual Convolutional Kernels for Lightweight Deep Neural Networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2022.
[13] 姚潇, 史叶伟, 霍冠英, 等. 基于神经网络结构搜索的轻量化网络构建[J]. 模式识别与人工智能,2021,34(11):1038-1048. DOI:10.16451/j.cnki.issn1003-6059.202111007.
[14] Pham H, Guan M, Zoph B, et al. Efficient neural architecture search via parameters sharing[C]. International conference on machine learning. Long Beach: PMLR, 2018: 4095-4104.
[15] 郝立扬. 基于量化卷积神经网络的模型压缩方法研究[D].成都: 电子科技大学,2020.DOI:10.27005/d.cnki.gdzku.2020.003279.
[16] Zhuang B, Shen C, Tan M, et al. Towards effective low-bitwidth convolutional neural networks[C]. Proceedings of the IEEE conference on computer vision and pattern recognition. Salt Lake City: IEEE, 2018: 7920-7928.
[17] Fan A, Stock P, Graham B, et al. Training with quantization noise for extreme model compression[J]. arXiv preprint arXiv:2004.07320, 2020.
[18] Choi J, Wang Z, Venkataramani S, et al. Pact: Parameterized clipping activation for quantized neural networks[J]. arXiv preprint arXiv:1805.06085, 2018.
[19] Jung S, Son C, Lee S, et al. Learning to quantize deep networks by optimizing quantization intervals with task loss[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 4350-4359.
[20] Steven K Esser, Jeffrey L McKinstry, Deepika Bablani, Rathinakumar Appuswamy, and Dharmendra S Modha. Learned step size quantization.arXiv preprint arXiv:1902.08153, 2019.
[21] Bhalgat Y, Lee J, Nagel M, et al. Lsq+: Improving low-bit quantization through learnable offsets and better initialization[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. Long Beach: IEEE, 2020: 696-697.
[22] Banner R, Nahshan Y, Hoffer E, et al. Post-training 4-bit quantization of convolution networks for rapid-deployment. arXiv 2018[J]. arXiv preprint arXiv:1810.05723.
[23] Fang J, Shafiee A, Abdel-Aziz H, et al. Post-training piecewise linear quantization for deep neural networks[C]. European Conference on Computer Vision. Online: Springer, Cham, 2020: 69-86.
[24] Choukroun Y, Kravchik E, Yang F, et al. Low-bit Quantization of Neural Networks for Efficient Inference[C]. ICCV Workshops. Seoul: IEEE, 2019: 3009-3018.
[25] Hinton G, Vinyals O, Dean J. Distilling the knowledge in a neural network[J]. arXiv preprint arXiv:1503.02531, 2015, 2(7).
[26] Phuong M, Lampert C. Towards understanding knowledge distillation[C]. International Conference on Machine Learning. Ottawa: PMLR, 2019: 5142-5151.
[27] Ji G, Zhu Z. Knowledge distillation in wide neural networks: Risk bound, data efficiency and imperfect teacher[J]. Advances in Neural Information Processing Systems, 2020, 33: 20823-20833.
[28] Cho J H, Hariharan B. On the efficacy of knowledge distillation[C]. Proceedings of the IEEE/CVF international conference on computer vision. Seoul: IEEE, 2019: 4794-4802.
[29] Cheng X, Rao Z, Chen Y, et al. Explaining knowledge distillation by quantifying the knowledge[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 12925-12935.
[30] Romero A, Ballas N, Kahou S E, et al. Fitnets: Hints for thin deep nets[J]. arXiv preprint arXiv:1412.6550, 2014.
[31] Shen Z, He Z, Xue X. Meal: Multi-model ensemble via adversarial learning[C]. Proceedings of the AAAI Conference on Artificial Intelligence. Hawaii: AAAI, 2019, 33(01): 4886-4893.
[32] Mirzadeh S I, Farajtabar M, Li A, et al. Improved knowledge distillation via teacher assistant[C]. Proceedings of the AAAI Conference on Artificial Intelligence. New York: IAAA, 2020, 34(04): 5191-5198.
[33] Xu G, Liu Z, Li X, et al. Knowledge distillation meets self-supervision[C]. European Conference on Computer Vision. Online: Springer, Cham, 2020: 588-604.
[34] Y . LeCun, J. S. Denker, and S. A. Solla, “Optimal brain damage,” in Proc. Adv. Neural Inf. Process. Syst. (NeurIPS), 1990, pp. 598–605.
[35] Srinivas S, Babu R V. Data-free parameter pruning for deep neural networks[J]. arXiv preprint arXiv:1507.06149, 2015.
[36] Han S, Pool J, Tran J, et al. Learning both weights and connections for efficient neural networks[J]. arXiv preprint arXiv:1506.02626, 2015.
[37] Liu Z, Xu J, Peng X, et al. Frequency-domain dynamic pruning for convolutional neural networks[C]. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montreal: NIPS,2018: 1051-1061.
[38] Dong X, Chen S, Pan S J. Learning to prune deep neural networks via layer-wise optimal brain surgeon[J]. arXiv preprint arXiv:1705.07565, 2017.
[39] Chen C, Tung F, Vedula N, et al. Constraint-aware deep neural network compression[C]. Proceedings of the European Conference on Computer Vision. Munich: Springer, 2018: 400-415.、
[40] Lin T, Stich S U, Barba L, et al. Dynamic model pruning with feedback[J]. arXiv preprint arXiv:2006.07253, 2020.
[41] Li H, Kadav A, Durdanovic I, et al. Pruning filters for efficient convnets[J]. arXiv preprint arXiv:1608.08710, 2016.
[42] Yu R, Li A, Chen C F, et al. Nisp: Pruning networks using neuron importance score propagation[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 9194-9203.
[43] He Y, Liu P, Wang Z, et al. Filter pruning via geometric median for deep convolutional neural networks acceleration[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 4340-4349.
[44] Lin M, Ji R, Wang Y, et al. Hrank: Filter pruning using high-rank feature map[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 1529-1538.
[45] Hu H, Peng R, Tai Y W, et al. Network trimming: A data-driven neuron pruning approach towards efficient deep architectures[J]. arXiv preprint arXiv:1607.03250, 2016.
[46] Lee N, Ajanthan T, Torr P H S. Snip: Single-shot network pruning based on connection sensitivity[J]. arXiv preprint arXiv:1810.02340, 2018.
[47] Wen W, Wu C, Wang Y, et al. Learning structured sparsity in deep neural networks[J]. Advances in neural information processing systems, 2016, 29: 2074-2082.
[48] Liu Z, Li J, Shen Z, et al. Learning efficient convolutional networks through network slimming[C]. Proceedings of the IEEE international conference on computer vision. Venice: IEEE, 2017: 2736-2744.
[49] Zhao C, Ni B, Zhang J, et al. Variational convolutional neural network pruning[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 2780-2789.
[50] Huang Z, Wang N. Data-driven sparse structure selection for deep neural networks[C]. Proceedings of the European conference on computer vision. Munich: Springer, 2018: 304-320.
[51] Lin S, Ji R, Yan C, et al. Towards optimal structured cnn pruning via generative adversarial learning[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 2790-2799.
[52] Lemaire C, Achkar A, Jodoin P M. Structured pruning of neural networks with budget-aware regularization[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 9108-9116.
[53] Wang Y, Zhang X, Xie L, et al. Pruning from scratch[C]. Proceedings of the AAAI Conference on Artificial Intelligence. New York: AAAI, 2020, 34(07): 12273-12280.
[54] Frankle J, Carbin M. The lottery ticket hypothesis: Finding sparse, trainable neural networks[J]. arXiv preprint arXiv:1803.03635, 2018.
[55] Liu Z, Mu H, Zhang X, et al. Metapruning: Meta learning for automatic neural network channel pruning[C]. Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019: 3296-3305.
[56] He Y, Lin J, Liu Z, et al. Amc: Automl for model compression and acceleration on mobile devices[C]. Proceedings of the European conference on computer vision. Munich: Springer, 2018: 784-800.
[57] Lin M, Ji R, Zhang Y, et al. Channel pruning via automatic structure search[J]. arXiv preprint arXiv:2001.08565, 2020.
[58] Guo S, Wang Y, Li Q, et al. Dmcp: Differentiable markov channel pruning for neural networks[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 1539-1547.
推荐专栏
🔥 手把手实现Image captioning
💯CNN模型压缩
💖模式识别与人工智能(程序与算法)
🔥FPGA—Verilog与Hls学习与实践
💯基于Pytorch的自然语言处理入门与实践

 算法)







动画)



:Jacobi 旋转法及其Python实现)
 第十二章 软件测试概述课后习题及其答案解析)





