目录
- 1.概述
- 2.代码实现
- 2.1.邻接矩阵存储图
- 2.2.邻接表存储图
- 2.3.测试
- 3.应用
1.概述
(1)在一给定的无向图 G = (V, E) 中,(u, v) 代表连接顶点 u 与顶点 v 的边,而 w(u, v) 代表此边的权重,若存在 T 为 E 的子集且为无循环图,使得联通所有结点的 w(T) 最小,则此 T 为 G 的最小生成树 (minimal spanning tree)。
(2)普利姆 (Prim) 算法是一种用于解决最小生成树问题的贪心算法,其主要思路如下:
- ① 选择任意一个顶点作为起始点,将其加入最小生成树中。
- ② 从已选择的顶点集合中选取一个顶点,该顶点与未选择的顶点构成的边权重最小,并且该边的另一端顶点未被选择,将该顶点和边加入最小生成树中。
- ③ 重复步骤 ②,直到最小生成树包含了图中的所有顶点。
(3)例如,对带权连通无向图 G 使用普利姆 (Prim) 算法构造最小生成树的过程如下:
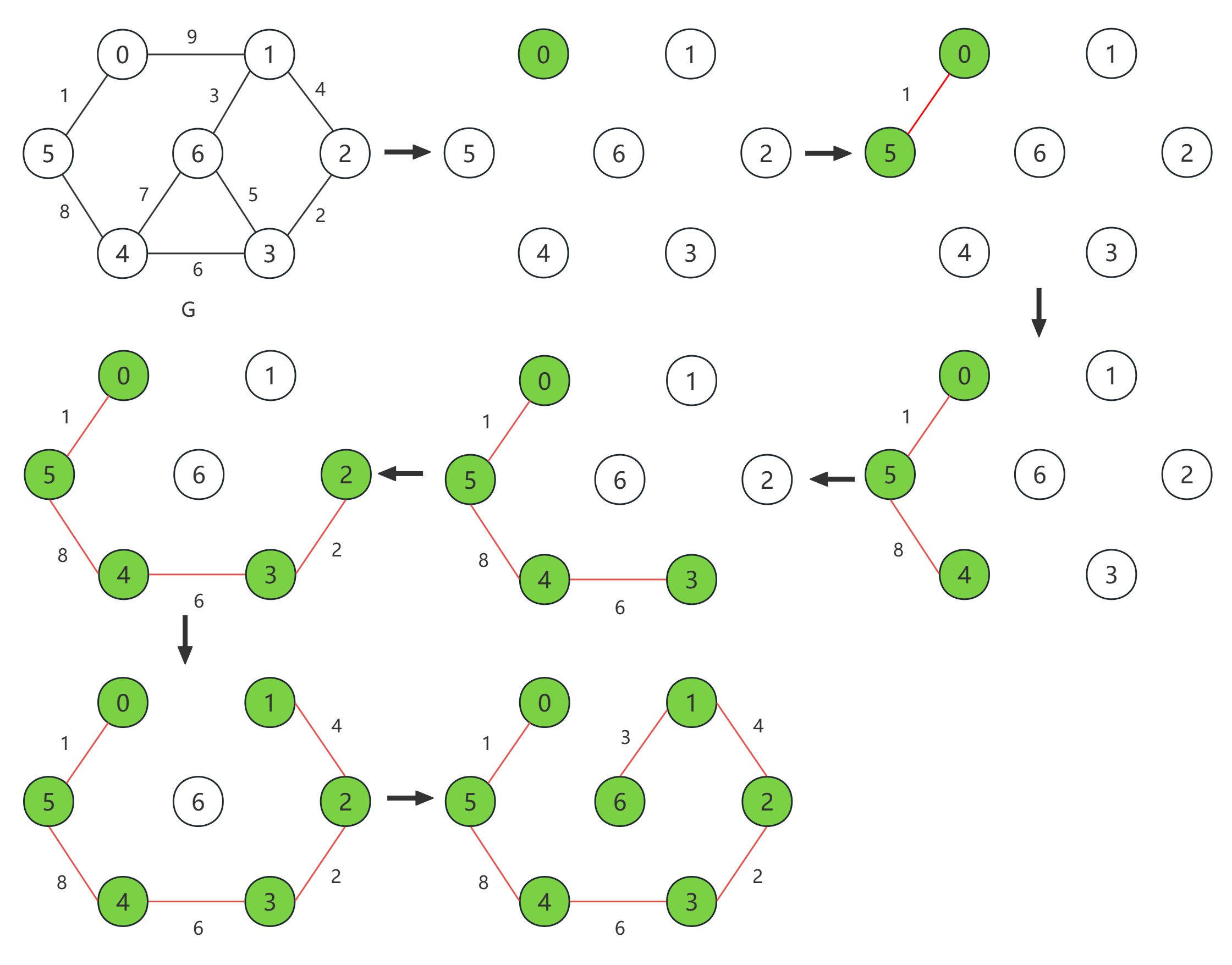
另外一种生成最小生成树的克鲁斯卡尔 (Kruskal) 算法可参考【算法】最小生成树——克鲁斯卡尔 (Kruskal) 算法这篇文章。
2.代码实现
2.1.邻接矩阵存储图
class Solution {// INF 表示两点之间没有连接,即无穷大int INF = Integer.MAX_VALUE;/*graph: 用于表示图的邻接矩阵返回值: 路径矩阵*/public int prim(int[][] graph) {//图中的顶点数int V = graph.length;// weight[i] 表示从 i 点到已访问集合的最小边权值int[] weight = new int[V];Arrays.fill(weight, INF);//标记节点是否在最小生成树中boolean[] mstSet = new boolean[V];// parent[i] 表示从 i 点到最小生成树的一条边int[] parent = new int[V];//从顶点 0 开始生成最小树weight[0] = 0;//根节点没有父节点parent[0] = -1;//访问 V - 1 个节点for (int i = 0; i < V - 1; i++) {//从未访问的节点中选择 weight 最小的节点 uint u = minKey(weight, mstSet);//将节点 u 标记为已访问mstSet[u] = true;//访问与 u 相邻的节点 vfor (int v = 0; v < V; v++) {//如果 v 未被访问过、u - v 之间有边、并且 u - v 之间的距离比原本的距离小if (!mstSet[v] && graph[u][v] != 0 && graph[u][v] != INF && graph[u][v] < weight[v]) {//将 u - v 之间的边加入最小生成树parent[v] = u;//标记从 v 到已访问集合的最小边权值weight[v] = graph[u][v];}}}//计算最小生成树的权值并返回int sum = 0;for (int i = 1; i < V; i++) {sum += weight[i];}//输出最小生成树的路径System.out.println("最小生成树的路径以及对应的权重依次为: ");for (int i = 1; i < V; i++) {System.out.println("(" + parent[i] + "-" + i + ") " + weight[i]);}return sum;}public int minKey(int[] weight, boolean[] mstSet) {//初始化 weight 的最小值和对应的节点int min = INF;int minIndex = -1;for (int v = 0; v < weight.length; v++) {//如果 v 节点未被访问,并且 v 节点到已访问集合的边的权值更小if (!mstSet[v] && weight[v] < min) {//更新最小值min = weight[v];//更新 weight 的最小值对应的节点minIndex = v;}}return minIndex;}
}
2.2.邻接表存储图
class Solution {// INF 表示两点之间没有连接,即无穷大int INF = Integer.MAX_VALUE;/*graph: 用于表示图的邻接表返回值: 最小生成树的权重*/public int prim(List<int[]>[] graph) {//图中的顶点数int V = graph.length;// weight[i] 表示从 i 点到已访问集合的最小边权值int[] weight = new int[V];Arrays.fill(weight, INF);//标记节点是否在最小生成树中boolean[] mstSet = new boolean[V];// parent[i] 表示从 i 点到最小生成树的一条边int[] parent = new int[V];//从顶点 0 开始生成最小树weight[0] = 0;//根节点没有父节点parent[0] = -1;//访问 V - 1 个节点for (int i = 0; i < V - 1; i++) {//从未访问的节点中选择 weight 最小的节点 uint u = minKey(weight, mstSet);//将节点 u 标记为已访问mstSet[u] = true;//访问与 u 相邻的节点 vfor (int[] node : graph[u]) {int v = node[0];int w = node[1];if (!mstSet[v] && w < weight[v]) {parent[v] = u;weight[v] = w;}}}//计算最小生成树的权值并返回int sum = 0;for (int i = 1; i < V; i++) {sum += weight[i];}//输出最小生成树的路径System.out.println("最小生成树的路径以及对应的权重依次为: ");for (int i = 1; i < V; i++) {System.out.println("(" + parent[i] + "-" + i + ") " + weight[i]);}return sum;}public int minKey(int[] weight, boolean[] mstSet) {//初始化 weight 的最小值和对应的节点int min = INF;int minIndex = -1;for (int v = 0; v < weight.length; v++) {//如果 v 节点未被访问,并且 v 节点到已访问集合的边的权值更小if (!mstSet[v] && weight[v] < min) {//更新最小值min = weight[v];//更新 weight 的最小值对应的节点minIndex = v;}}return minIndex;}
}
2.3.测试
(1)本测试中的加权无向图如下所示:
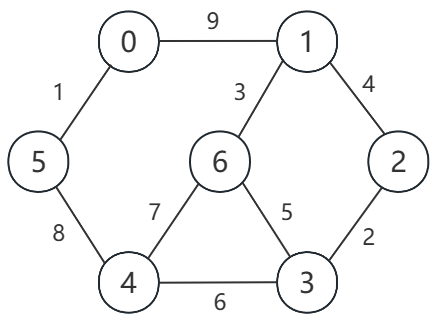
(2)邻接矩阵的测试代码如下:
class Test {public static void main(String[] args) {//图的顶点数int n = 7;int[][] graph = new int[n][n];//初始化邻接矩阵,初始化为 Integer.MAX_VALUE 表示不可达for (int i = 0; i < n; i++) {Arrays.fill(graph[i], Integer.MAX_VALUE);graph[i][i] = 0;}//添加图的边graph[0][1] = 9;graph[0][5] = 1;graph[1][0] = 9;graph[1][2] = 4;graph[1][6] = 3;graph[2][1] = 4;graph[2][3] = 2;graph[3][2] = 2;graph[3][4] = 6;graph[3][6] = 5;graph[4][3] = 6;graph[4][5] = 8;graph[4][6] = 7;graph[5][0] = 1;graph[5][4] = 8;graph[6][1] = 3;graph[6][3] = 5;graph[6][4] = 7;Solution solution = new Solution();int sum = solution.prim(graph);System.out.println("最小生成树的权重为: " + sum);}
}
输出结果如下:
最小生成树的路径以及对应的权重依次为:
(2-1) 4
(3-2) 2
(4-3) 6
(5-4) 8
(0-5) 1
(1-6) 3
最小生成树的权重为: 24
(3)邻接表的测试代码如下:
class Test {public static void main(String[] args) {//图的顶点数int n = 7;List<int[]>[] graph = new ArrayList[n];//初始化邻接表for (int i = 0; i < n; i++) {graph[i] = new ArrayList<>();}//添加图的边graph[0].add(new int[]{1, 9});graph[0].add(new int[]{5, 1});graph[1].add(new int[]{0, 9});graph[1].add(new int[]{2, 4});graph[1].add(new int[]{6, 3});graph[2].add(new int[]{1, 4});graph[2].add(new int[]{3, 2});graph[3].add(new int[]{2, 2});graph[3].add(new int[]{4, 6});graph[3].add(new int[]{6, 5});graph[4].add(new int[]{3, 6});graph[4].add(new int[]{5, 8});graph[4].add(new int[]{6, 7});graph[5].add(new int[]{0, 1});graph[5].add(new int[]{4, 8});graph[6].add(new int[]{1, 3});graph[6].add(new int[]{3, 5});graph[6].add(new int[]{4, 7});Solution solution = new Solution();int sum = solution.prim(graph);System.out.println("最小生成树的权重为: " + sum);}
}
输出结果如下:
最小生成树的路径以及对应的权重依次为:
(2-1) 4
(3-2) 2
(4-3) 6
(5-4) 8
(0-5) 1
(1-6) 3
最小生成树的权重为: 24
3.应用
(1)求图的最小生成树许多实际应用,例如城市之间的交通工程造价最优问题就是一个最小生成树问题。
(2)大家可以去 LeetCode 上找相关的最小生成树的题目来练习,或者也可以直接查看 LeetCode 算法刷题目录 (Java) 这篇文章中的最小生成树章节。如果大家发现文章中的错误之处,可在评论区中指出。







动画)



:Jacobi 旋转法及其Python实现)
 第十二章 软件测试概述课后习题及其答案解析)






