一、微网系统运行优化模型
微电网优化模型介绍:
微电网多目标优化调度模型简介_IT猿手的博客-CSDN博客
二、多目标灰狼优化算法MOGWO
多目标灰狼优化算法MOGWO简介:

三、多目标灰狼优化算法MOGWO求解微电网多目标优化调度
(1)部分代码
close all;
clear ;
clc;
global P_load; %电负荷
global WT;%风电
global PV;%光伏
%%
addpath('./NSDBO/')%添加算法路径
TestProblem=1;
MultiObj = GetFunInfo(TestProblem);
MultiObjFnc=MultiObj.name;%问题名
% Parameters
params.Np = 100; % Population size
params.Nr = 200; % Archive size
params.maxgen = 100; % Maximum number of iteration
params.ngrid = 20; % Number of grids in each dimension
[Xbest,Fbest] = MOGWO(params,MultiObj);%% 画结果图ParetoFont
figure(1)
plot(Fbest(:,1),Fbest(:,2),'ro');
legend('MOGWO');
xlabel('运行成本')
ylabel('环境保护成本')
saveas(gcf,'./Picture/ParetoFont.jpg') %将图片保存到Picture文件夹下面%% 比较不同目标函数寻优对调度结果的影响
%idxn=1 第1种.将两个目标函数值归一化相加,取相加后最小的目标值的粒子,即寻找折衷解并画图
%idxn=2 第2种寻找总成本最低时的解并画图
%idxn=3 第3种寻找运行成本最低时的解并画图
%idxn=4 第4种寻找环境保护成本最低时的解并画图
idxn=1;
pg=plotFigure(Xbest,Fbest,idxn);
(2)部分结果
pareto前沿:
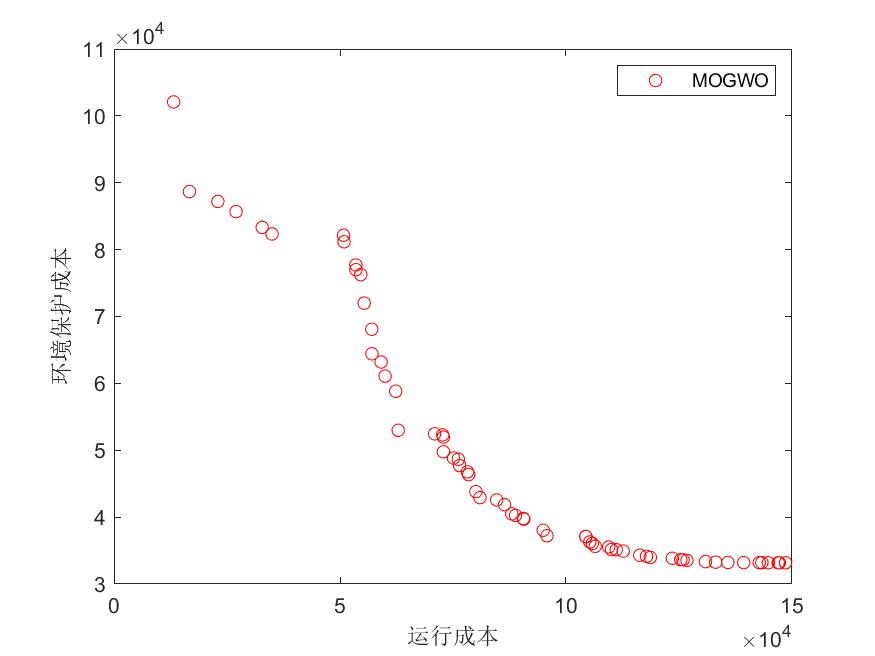
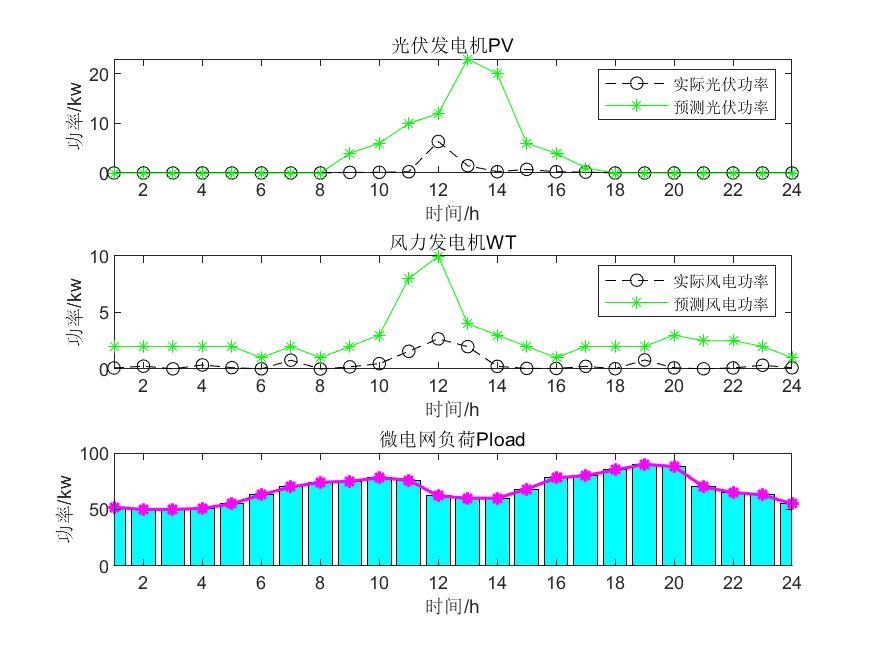
第1种.将两个目标函数值归一化相加,取相加后最小的目标值的粒子,即寻找折衷解并画图



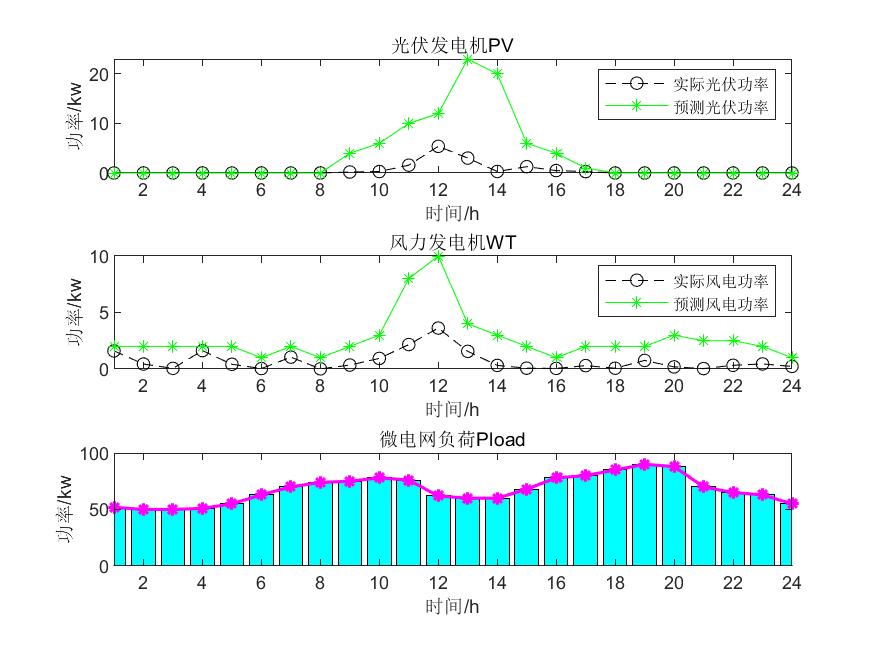
第2种寻找总成本最低时的解并画图



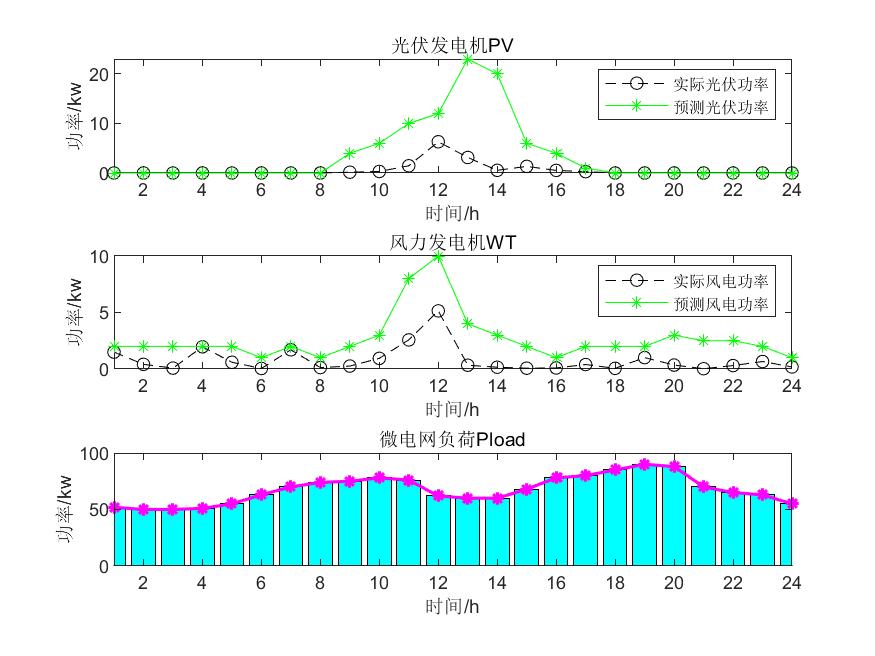
第3种寻找运行成本最低时的解并画图



第4种寻找环境保护成本最低时的解并画图




四、完整MATLAB代码


)








安装JDK环境)
)
)




)
