【数据结构】栈

1.58.33

栈

栈
- 栈的概念及基本结构
- 栈的存储
- 栈的基本操作
- - 栈的置空初始化---StackInit()
  - 栈的初始化2.0---给栈开辟一点空间StackInit1()
  - 栈的销毁---StackDestory()
  - 入栈----StackPush()
  - 出栈----StackPop()
  - 获取栈中元素的数量---StackSize()
  - 判断栈是否为空---StackEmpty()
  - 获取栈顶元素---StackTop
  - 栈元素的遍历
- 程序的运行
- - 头文件---stack.h
  - 源文件编写函数---stack.c
  - 源文件编写--在主函数中运行 test.c
  - 运行结果
栈的应用---括号的匹配
- 题目---Leetcode20.有效的括号
- 举例认识---有效的括号
- 找出规律

栈

栈的概念及基本结构

栈：栈式一种特殊的线性表，只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除的一端称为栈顶，另一端称为栈底。栈中的数据元素遵循后进先出的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，插入数据在栈顶。
出栈：栈的删除操作叫出栈。出栈元素在栈顶。

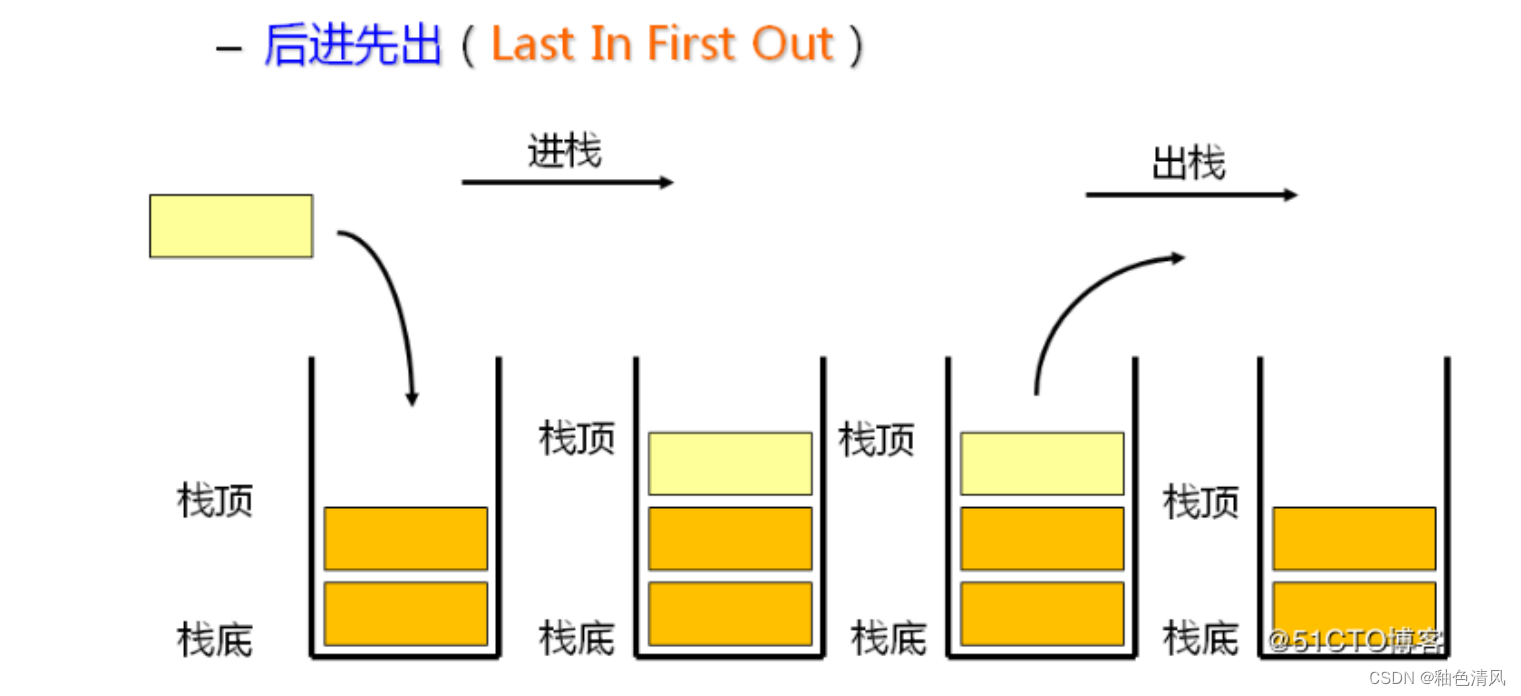
栈的存储

栈的存储方式有两种：顺序栈和链栈，即栈的顺序存储和链式存储。

采用顺序存储的栈称为顺序栈，它利用一组地址连续的存储单元存放自栈底到栈顶的元素，同时附设一个指针（top）指示当前栈顶的位置。

对于栈数据结构，采用顺序栈更方便进行压栈尤其是出栈，所以本次主要说明利用顺序栈来实现栈的基本操作。

同时这里，利用一组地址连续的存储单元进行存放，同顺序表的存储一样，分为静态存储和动态存储。

在静态存储中，即利用宏定义给定一个顺序表的大小，对于后续操作，尤其是入栈，如果入若干次栈，而由于顺序表的内存空间有限，那么就会直接报错而无法进行后续操作。

在动态存储中，就比较灵活了，正好可以解决这个问题。在动态存储中，我们利用定义的指针在堆上开辟一块内存空间，若空间大小不够，我们可以进行扩容操作。但同时我们动态存储时，也要注意，在栈操作最后要注意堆上内存空间的释放。

typedef int datatype;
typedef struct Stack
{datatype *a;int top;int capacity;
}Stack;

可以形象地来理解以下：

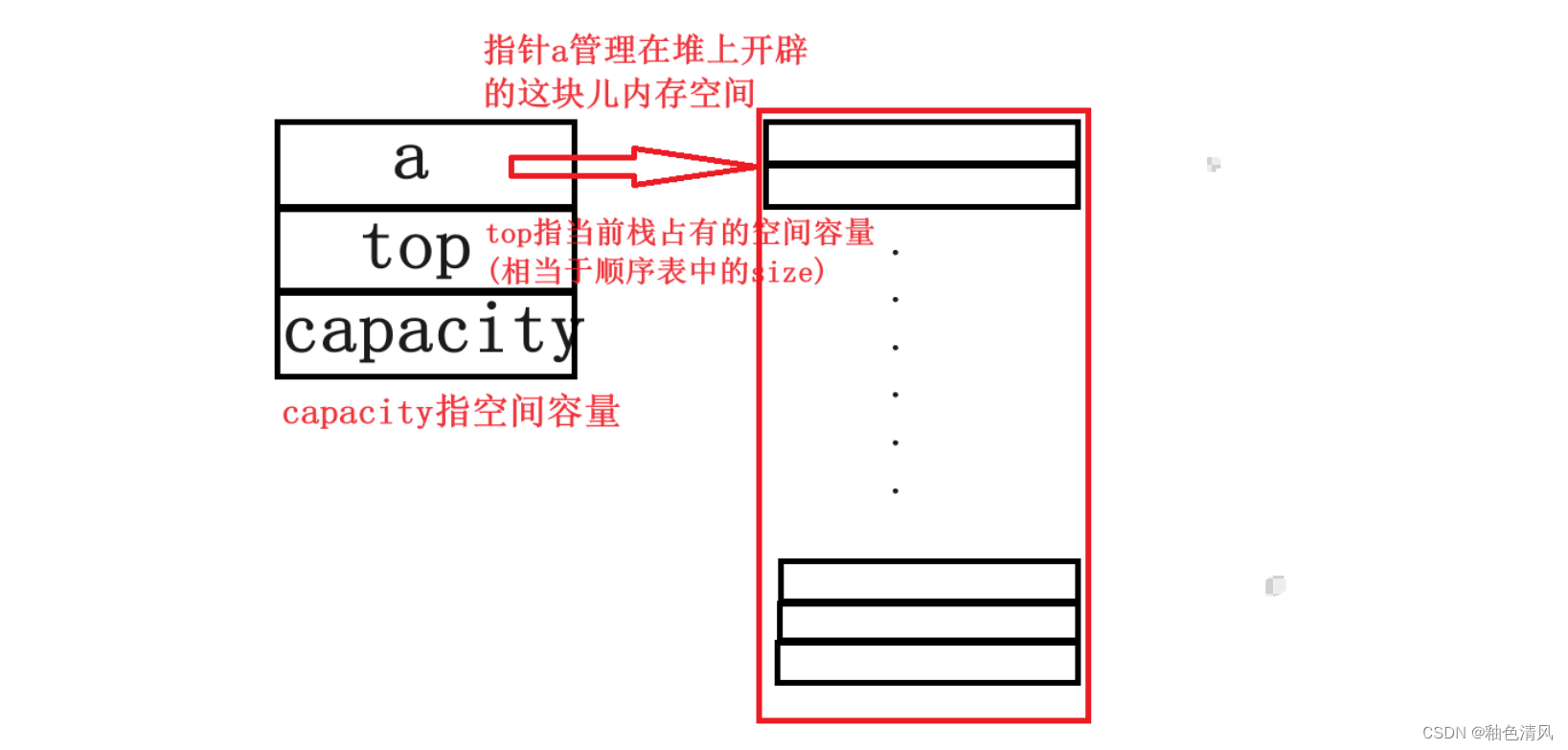
栈的基本操作

栈的置空初始化—StackInit()

void StackInit(Stack *ps)
{assert(ps);ps->a=NULL;ps->top=0;ps->capacity=0;
}

这里用到了assert函数，下面几乎每个函数也都会用到。在这里简单说明一下这个函数。
assert函数即断言函数，“断言”在语文中的意思是“断定”、“十分肯定地说”，在编程中是指对某种假设条件进行检测，如果条件成立就不进行任何操作，如果条件不成立就捕捉到这种错误，并打印出错误信息，终止程序执行。
所在头文件：<assert.h>
函数原型：void assert (int expression);
参数：expression即要检测的表达式
返回值：无返回值
如果expression的结果为 0（条件不成立），那么断言失败，表明程序出错，assert() 会向标准输出设备（一般是显示器）打印一条错误信息，并调用 abort() 函数终止程序的执行。
assert()函数相比于return ，更加直接‘暴力“，如果条件不成立，那么程序就将终止。
如果expression的结果为非 0（条件成立），那么断言成功，表明程序正确，assert() 不进行任何操作。

在这里，我们对传入的指针进行断言，如果为空指针，那么程序终止退出程序，若不为空指针，那么不进行任何的操作，程序继续往下执行。

栈的初始化2.0—给栈开辟一点空间StackInit1()

void StackInit1(Stack *ps)
{assert(ps);ps->a=(datatype *)malloc(sizeof(Stack)*4);//开辟4个空间ps->capacity=4;
}

栈的销毁—StackDestory()

因为malloc函数是在堆上开辟的内存空间，而对于堆上的内存空间比较灵活，系统不会自动释放，而需要我们手动释放，所以在一个函数中既然开辟了栈，那就一定要记得最后销毁。

void StackDestory()
{assert(ps);free(p->a);ps->a=NULL;ps->top=ps->capacity=0;
}

入栈----StackPush()

void StackPush(Stack *ps,datatype x)
{assert(ps);//判断栈的空间是否已满if(ps->top==ps->capacity){//扩容为原容量的2倍datatype *tmp=(datatype *)relloc(ps->a,sizeof(Stack)*capacity*2);ps->capacity=ps->capacity*2;}ps->a[ps->top]=x;ps->top++;
}

出栈----StackPop()

void StackPop(Stack *ps)
{assert(ps);//判断当前栈是否为空，若空则无法出栈，退出程序assert(ps->top >0);ps->top--;
}

获取栈中元素的数量—StackSize()

int StackSize(Stack *ps)
{assert(ps);return ps->top;
}

判断栈是否为空—StackEmpty()

bool StackEmpty()
{assert(ps);//若ps->top==0,为真，则返回True；若ps->top！=0，为假，则返回Falsereturn ps->top == 0;
}

获取栈顶元素—StackTop

datatype StackTop(Stack *ps)
{assert(ps);//判断栈是否为空assert(ps->top>0);return ps->a[ps->top - 1];    
}

栈元素的遍历

栈结构的特点是，后进先出，即后进的元素先进行遍历。所以我们就需要出栈，也就是逐渐删除栈顶元素进行遍历。
首先，我们先在测试函数中创立一个栈：

void TestStack()
{Stack s;StackInit(&s);StackInit1(&s);StackPush(&s,1);StackPush(&s,2);StackPush(&s,3);StackPush(&s,4);StackPush(&s,4);StackDestory(&s);
}

然后，我们一次删除栈顶元素，进行栈的遍历：

void TestStack()
{Stack s;StackInit(&s);StackInit1(&s);StackPush(&s,1);StackPush(&s,2);StackPush(&s,3);StackPush(&s,4);StackPush(&s,4);while(ps->top){printf("%d",StackTop(&s));StackPop();}printf("\n");StackDestory(&s);
}

程序的运行

头文件—stack.h

#pragma once
#define _CER_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>   //malloc函数
#include <assert.h>    //assert函数
#include <stdbool.h>   //bool类型typedef int datatype;
typedef struct Stack
{datatype* a;int top;int capacity;
}Stack;void StackInit(Stack* ps); //置空
void StackInit1(Stack* ps);  //初始化
void StackDestory(Stack* ps);   //销毁
void StackPush(Stack* ps, datatype x); //入栈
void StackPop(Stack* ps);//出栈
int StackSize(Stack* ps); //获取栈中元素的多少
bool StackEmpty(Stack* ps); //判断是否栈空
datatype StackTop(Stack* ps);//获取栈顶元素

源文件编写函数—stack.c

#include "stack.h"//栈置空
void StackInit(Stack* ps)
{assert(ps);ps->a = NULL;ps->top = 0;ps->capacity = 0;
}//栈初始化
void StackInit1(Stack* ps)
{assert(ps);ps->a = (datatype*)malloc(sizeof(Stack) * 4);//开辟4个空间ps->capacity = 4;
}//栈的销毁
void StackDestory(Stack *ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->top = ps->capacity = 0;
}//入栈
void StackPush(Stack* ps, datatype x)
{assert(ps);//判断栈的空间是否已满if (ps->top == ps->capacity){//扩容为原容量的2倍datatype* tmp = (datatype*)realloc(ps->a, sizeof(Stack) * ps->capacity * 2);ps->capacity = ps->capacity * 2;}ps->a[ps->top] = x;ps->top++;
}//出栈
void StackPop(Stack* ps)
{assert(ps);//判断当前栈是否为空，若空则无法出栈，退出程序assert(ps->top > 0);ps->top--;
}//获取栈中元素的数量
int StackSize(Stack* ps)
{assert(ps);return ps->top;
}//判断栈是否为空
bool StackEmpty(Stack *ps)
{assert(ps);//若ps->top==0,为真，则返回True；若ps->top！=0，为假，则返回Falsereturn ps->top == 0;
}//获取栈顶元素
datatype StackTop(Stack* ps)
{assert(ps);//判断栈是否为空assert(ps->top > 0);return ps->a[ps->top - 1];
}

源文件编写–在主函数中运行 test.c


#include "stack.h"
//测试函数的编写---栈元素的遍历
void TestStack()
{Stack s;StackInit(&s);StackInit1(&s);StackPush(&s, 1);StackPush(&s, 2);StackPush(&s, 3);StackPush(&s, 4);StackPush(&s, 5);while (( & s)->top){printf("%d", StackTop(&s));StackPop(&s);}printf("\n");StackDestory(&s);
}
//主函数
int main()
{TestStack();return 0;
}