手写堆,而非stl中的堆
如何手写一个堆?
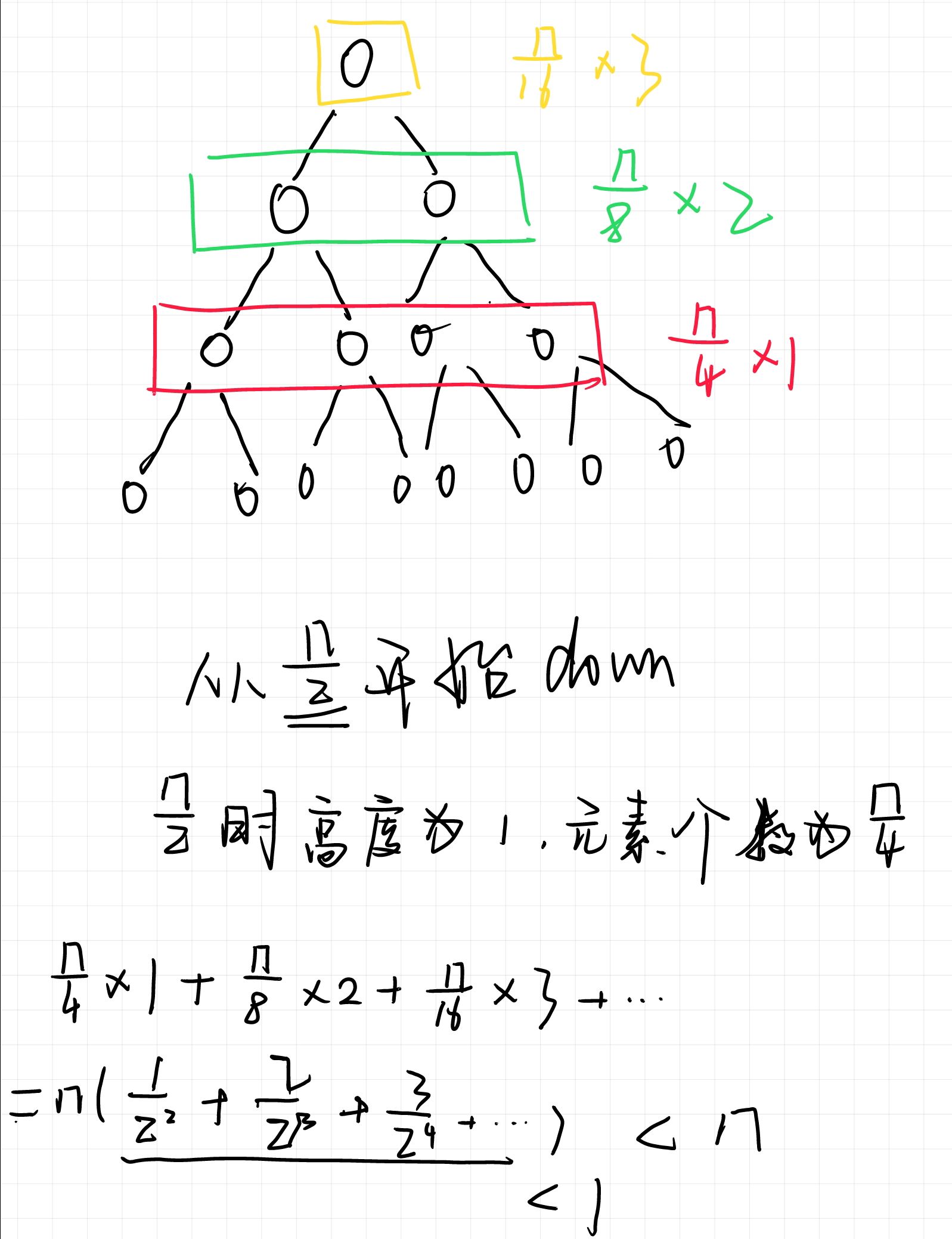
//将数组建成堆 <O(n)
for (int i = n / 2;i;i--) //从n/2开始down
down(i);
从n/2元素开始down,最下面一层元素的个数是n/2,其余上面的元素的个数是n/2,从最下面一层到最高层,每层元素的个数是n/2^m【m从下到上,从1计算,m=1时是最下面一层】,时间复杂度就是元素个数*高度【高度从下到上,从0计算】
性质
1.堆是一棵完全二叉树【除叶子结点之外,所有结点都是非空的】
2.小根堆:每个点的值都是小于等于其左右两个儿子的,根结点就是整个数据中的最小值
静态数组存储——一维数组
用一个一维数组来存,根结点放在数组开头,1号点是根结点,结点x的左儿子下标为2x,右儿子下标为2x+1
两个基本操作
对于所有的堆操作而言,每个操作都可以使用这两个操作构建。
down(x) 向下调整——从下往上down一次就变成一个堆
大数位于上面,需要向下移
每次与其两个儿子进行比较,找到较小的儿子与其进行交换,直到小于所有的儿子为止【该结点的子结点都大于该结点】
//递归实现
void down(int u) {
int t = u;//用t表示三个点中的最小值
if (u * 2 <= size1 && h[u * 2] < h[t])//先判断是否有左儿子,然后判断左儿子是否小于其本身,如果成立,交换
t = u * 2;
if (u * 2 + 1 <= size1 && h[u * 2 + 1] < h[t])//再判断是否有右儿子,然后判断右儿子是否小于其本身,如果成立,交换
t = u * 2 + 1;
//最终,t存的就是三个点中最小的结点编号
if (u != t) {//如果u!=t,说明根结点就不是最小的,需要交换
swap(h[u], h[t]);//交换
down(t);//递归,交换之前h[t]<=h[u],交换之后h[t]>h[u],h[t]中存的是大数,对其再进行down操作,即递归
}
return;
}
up(x) 向上调整
小数位于下面,需要向上移
每次只需要与其根结点比较,如果小于其根结点,就与其根结点进行交换,直到>=其根结点为止
//循环实现
void up(int u) {
while (u / 2 && h[u / 2] > h[u]) {//u的父结点为u/2,父结点存在且大于本身,交换
swap(h[u / 2], h[u]);
u = u / 2;
}
return;
}
操作
【前三最重要】
【下标从1开始】
1.向集合中插入一个数
在整个堆的最后一个位置插入,然后再向上调整
heap[++size]=x;
up(size);
2.求集合中的最小值
heap[1];
3.删除最小值
用整个堆的最后一个元素覆盖掉堆顶的元素,然后size--,然后向下调整
因为删去最后一个结点特别容易,而删除根结点却不易
heap[1]=heap[size];
size--;
down(1);
4.删除任意一个元素
用堆的最后一个结点覆盖该结点,然后size--,然后向下调整(变大)、向上调整(变小),二选一执行
heap[k]=heap[size];
size--;
down(k);//变大
up(k);//变小
5.修改任意一个操作
heap[k]=x;
down(k);//变大
up(k);//变小
例题——堆排序
题目描述
输入一个长度为n的整数数列,从小到大输出前m小的数。
输入格式
第一行包含整数n和m。
第二行包含n个整数,表示整数数列。
输出格式
共一行,包含m个整数,表示整数数列中前m小的数。
数据范围
1≤m≤n≤10^5,
1≤数列中元素≤10^9
输入样例
5 3
4 5 1 3 2
输出样例
1 2 3
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
int n, m;
int h[N], size1;//h[N]就是heap[N],size1存储当前有多少个元素
int main() {
scanf("%d%d", &n, &m);
for (int i = 1;i <= n;i++)
scanf("%d", &h[i]);
size1 = n;
//将数组建成堆 <O(n)
for (int i = n / 2;i;i--) //从n/2开始down
down(i);
while (m--) {
printf("%d ", h[1]);//每次输出堆顶元素,并将其删去
h[1] = h[size1];
size1--;
down(1);
}
return 0;
}
例题——模拟堆[包含映射]
增加两个数组
使用两个数组维护两个映射关系,ph[k] 存第k个插入的点在堆中的下标,hp[k] 存堆中下标为k的点是第几个插入的点
增加的原因
因为按第几个插入元素更改内容,需要知道第i个插入的元素在堆中的下标,所以需要ph的存在,而因为元素在进行down与up操作时,使得ph内容与实际堆的元素不对应,所以要改变ph,而改变ph应该知道,每一个下标对应的插入元素是第几个,所以需要hp的存在。每次交换位置时应该共同维护这两个数组。
交换操作
void heap_swap(int a, int b) {
swap(ph[hp[a]], ph[hp[b]]);//交换指向
swap(hp[a], hp[b]);
swap(h[a], h[b]);
return;
}
交换堆中的两个元素时,hp 和 ph 也改变。先改变 hp 和 ph 中的内容,然后改变这两个结点中的值。先根据交换的下标找到对应的 hp,并以两个 hp 元素值作为 ph 的下标,交换这2个 ph 元素值。之后根据下标交换 hp。
swap(ph[hp[a]], ph[hp[b]]);为什么这里的ph的下标是hp的元素值而不是堆中元素的编号?
因为ph的下标k的含义【即ph[k]的k的含义】是第k个插入的点,所以我们要找到第k个插入的点而不是堆中下标为k的点。
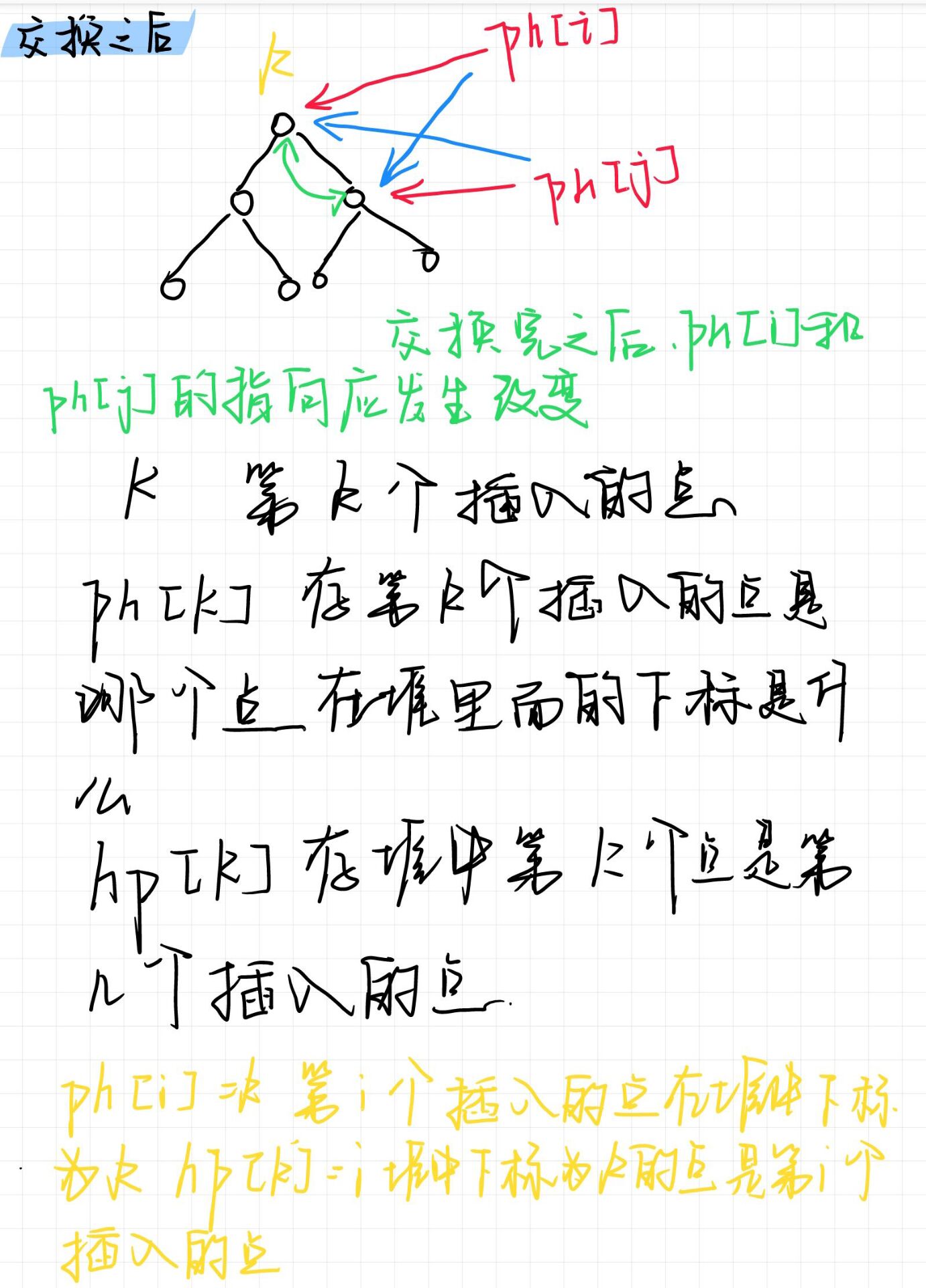
改变后的操作
up 操作
手写的heap_swap函数代替原来的swap函数
void up(int u) {
while (u / 2 && h[u / 2] > h[u]) {//u的父结点为u/2,父结点存在且大于本身,交换
heap_swap(u / 2, u);
u = u / 2;
}
return;
}
down 操作
手写的heap_swap函数代替原来的swap函数
void down(int u) {
int t = u;//用t表示三个点中的最小值
if (u * 2 <= size1 && h[u * 2] < h[t])//先判断是否有左儿子,然后判断左儿子是否小于其本身,如果成立,交换
t = u * 2;
if (u * 2 + 1 <= size1 && h[u * 2 + 1] < h[t])//再判断是否有右儿子,然后判断右儿子是否小于其本身,如果成立,交换
t = u * 2 + 1;
//最终,t存的就是三个点中最小的结点编号
if (u != t) {//如果u!=t,说明根结点就不是最小的,需要交换
heap_swap(u, t);//交换
down(t);
}
return;
}
向集合中插入一个数
添加hp和ph数组中的映射关系
scanf("%d", &x);//向堆中插入x
size1++;
m++;
ph[m] = size1;
hp[size1] = m;
h[size1] = x;
up(size1);
输出集合中的最小值
printf("%d\n", h[1])
删除最小值
手写的heap_swap函数代替原来的swap函数
heap_swap(1, size1);
size1--;
down(1);
删除第k个插入的元素
scanf("%d", &k);//输入k
k = ph[k];//找到第k个插入的元素在堆中的下标,然会对其进行删除
heap_swap(k, size1);//用堆中最后一个元素覆盖找到的元素,然会进行调整
size1--;
down(k), up(k);
修改第k个插入的元素
scanf("%d%d", &k, &x);//输入k和修改后的值x
k = ph[k];//找到第k个插入的元素在堆中的下标,然后修改其值,修改后进行调整
h[k] = x;
down(k), up(k);
题目描述
维护一个集合,初始时集合为空,支持如下几种操作:
“I x”,插入一个数x;
“PM”,输出当前集合中的最小值;
“DM”,删除当前集合中的最小值(当最小值不唯一时,删除最早插入的最小值);
“D k”,删除第k个插入的数;
“C k x”,修改第k个插入的数,将其变为x;
现在要进行N次操作,对于所有第2个操作,输出当前集合的最小值。
输入格式
第一行包含整数N。
接下来N行,每行包含一个操作指令,操作指令为”I x”,”PM”,”DM”,”D k”或”C k x”中的一种。
输出格式
对于每个输出指令“PM”,输出一个结果,表示当前集合中的最小值。
每个结果占一行。
数据范围
1≤N≤10^5
−10^9≤x≤10^9
数据保证合法。
输入样例
8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM
输出样例
-10
6
#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
const int N = 100010;
int h[N], ph[N], hp[N], size1;//h[N]就是heap[N],size1存储当前有多少个元素,ph[k]存第k个插入数组的下标
//ph[j]=k【第j次插入数组的数的下标是k】,hp[k]=j【下标为k的数是第j次插入数组中的数】
void heap_swap(int a, int b) {
swap(ph[hp[a]], ph[hp[b]]);//交换指向
swap(hp[a], hp[b]);
swap(h[a], h[b]);
return;
}
void down(int u) {
int t = u;//用t表示三个点中的最小值
if (u * 2 <= size1 && h[u * 2] < h[t])//先判断是否有左儿子,然后判断左儿子是否小于其本身,如果成立,交换
t = u * 2;
if (u * 2 + 1 <= size1 && h[u * 2 + 1] < h[t])//再判断是否有右儿子,然后判断右儿子是否小于其本身,如果成立,交换
t = u * 2 + 1;
//最终,t存的就是三个点中最小的结点编号
if (u != t) {//如果u!=t,说明根结点就不是最小的,需要交换
heap_swap(u, t);//交换
down(t);
}
return;
}
void up(int u) {
while (u / 2 && h[u / 2] > h[u]) {//u的父结点为u/2,父结点存在且大于本身,交换
heap_swap(u / 2, u);
u = u / 2;
}
return;
}
int main() {
int n, m = 0;
scanf("%d", &n);
while (n--) {
char op[10];
int k, x;
scanf("%s", op);
if (!strcmp(op, "I")) {
scanf("%d", &x);
size1++;
m++;
ph[m] = size1;
hp[size1] = m;
h[size1] = x;
up(size1);
}
else if (!strcmp(op, "PM"))
printf("%d\n", h[1]);
else if (!strcmp(op, "DM")) {
heap_swap(1, size1);
size1--;
down(1);
}
else if (!strcmp(op, "D")) {
scanf("%d", &k);
k = ph[k];
heap_swap(k, size1);
size1--;
down(k), up(k);
}
else {
scanf("%d%d", &k, &x);
k = ph[k];
h[k] = x;
down(k), up(k);
}
}
return 0;
}

)
)


——返回一组数字中所有和为 0 且不重复的三元组)





)

JPA 的测试)
)

)


)