大家好,我是怒码少年小码。
从本篇开始,我们就要开始算法的新篇章了——四大思想:滑动窗口、贪心、回溯、动态规划。现在,向我们迎面走来的是——滑动窗口思想!😝
滑动窗口思想
概念
在数组双指针里,我们介绍过"对撞型"和"快慢型"两种方式,而滑动窗口思想就是快慢型的特例。
实际使用
计算机网络中有滑动窗口协议(Sliding Window Protocol),该协议是TCP实现流量控制等的核心策略之一。事实上与流量控制、熔断、限流、超时等场景下都会首先从滑动窗口的角度思考问题,例如hystrix、sentinel等框架等都使用了这种思想。
理解
这个思想其实很好理解,如下图,假如窗口的大小是3,当不断有新数据来时,我们会维护一个大小为3的一个区间,超过3的就将新的放入老的移走。
这个过程有点像火车在铁轨上跑,原始数据可能保存在一个很大的空间里(铁轨),但是我们标记的小区间就像一列长度固定的火车,一直向前走。
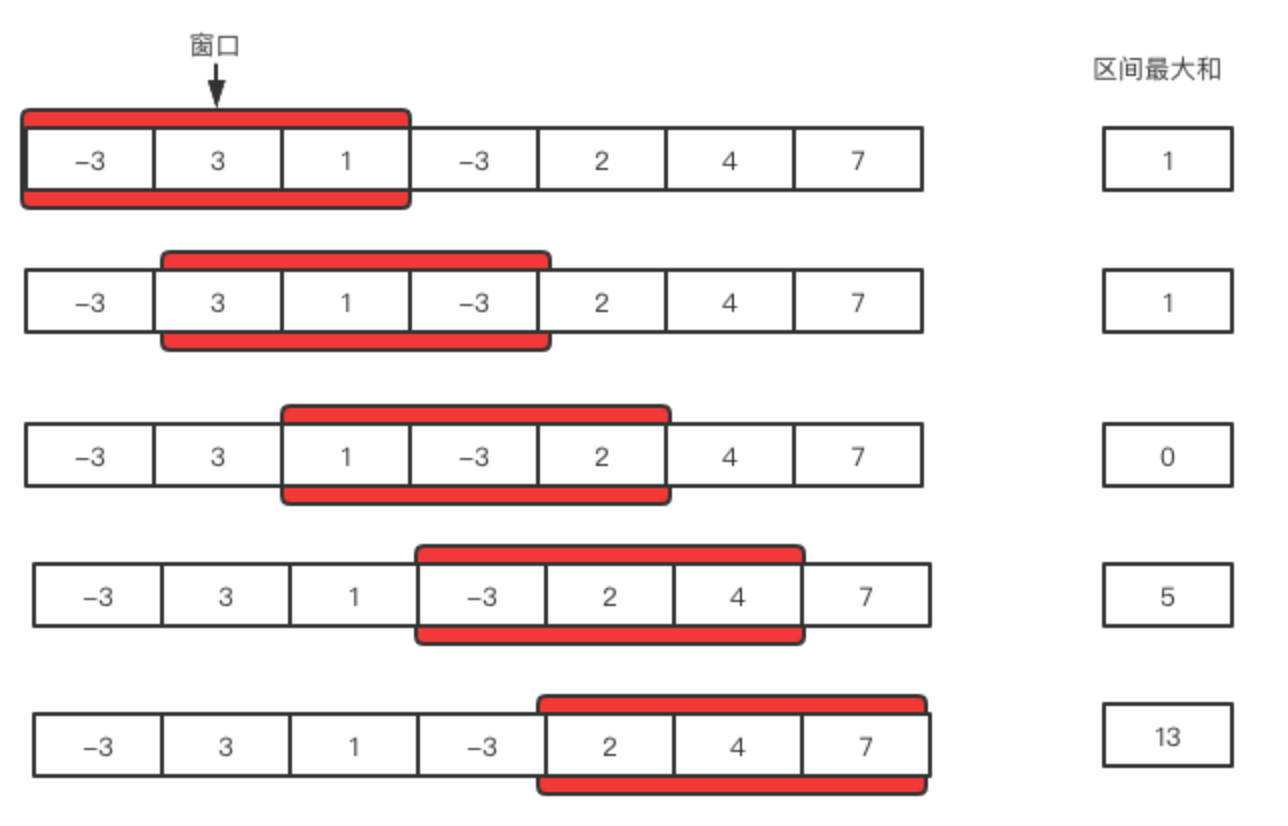
有了区间,就可以造题了,例如让你找序列上三个连续数字的最大和是多少、子数组平均数是多少(LeetCode643)等等。
窗口和滑动的含义:
- 窗口:窗口其实就是两个变量
left和right之间的元素,也可以理解为一个区间。窗口大小不一定固定,思考两种场景:
-
如果是固定的,一般要先确定窗口是否越界,再执行逻辑处理。则一般会让你求哪个窗口的元素最大、最小、平均值、和最大、和最小等类型的问题
-
如果是可变的窗口,一般先判断是否满足要求,再执行逻辑处理。则一般要求一个序列里最大、最小窗口是什么
- 滑动:说明这个窗口是移动的,事实上移动的仍然是
left和right两个变量,而不是序列中的元素。当变量移动时,其中间的元素必然会发生变化,因此就有这种不断滑动的效果.
注意事项
- 解题最终要落实到数组上,特别需要注意边界处理
- 有些元素的比较、判断等比较麻烦,要借助集合等工具,而且处理过程中还有一些技巧(常见方法的使用等)
- 堆,堆结构非常适合在流数据中找固定区间内的最大、最小等问题。因此滑动窗口经常和堆一起使用可以完美解决很多复杂问题.
那双指针和滑动窗口啥区别呢?
答:根据性质看到,滑动窗口是双指针的一种类型,主要关注两个指针之间元素的情况,范围更小一些,而双指针的应用范围更大,花样也更多。
入门小题
LeetCode 643:给你一个由 n 个元素组成的整数数组 nums 和一个整数 k。请你找出平均数最大且 长度为 k 的连续子数组,并输出该最大平均数。
先自己思考一下,不难但是想要完全做对还是要细心。例如我一开始就是先定义一个变量max保存最大值,然后left和right保存窗口两端。只要right不到数组边界,滑动窗口每次一变我就计算窗口内的元素之和,然后和max比较看看是否保存。
但是我一开始把max定为0,忽略数组内k个最大连续组序列的和是负数的情况。力扣上我又换回C++用INT_MIN来定义结果是直接超时了啊哈哈哈😁。正确代码如下:
public double findMaxAverage(int[] nums, int k) {if(k > nums.length || nums.length < 1 || k < 0){return 0;}int len = nums.length;int windowSum = 0;//先求出第一个窗口内的元素和for(int i = 0 ; i < k ;i++){windowSum = windowSum + nums[i];}//然后依次遍历,知道right达到数组边界,每次窗口变化选择变化前后最大的保存int maxSum = windowSum;for(int right = k ; right < len ; right++){windowSum = windowSum + nums[right] - nums[right - k];maxSum=Math.max(maxSum,windowSum);}return (double) maxSum / k;
}
最长连续递增序列
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
示例 1:
- 输入:nums = [1,3,5,4,7]
- 输出:3
- 解释:最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
- 输入:nums = [2,2,2,2,2]
- 输出:1
- 解释:最长连续递增序列是 [2], 长度为1。
思路:如果当前遍历到的元素比它左边的那一个元素要严格大,right就增加;
否则就将left跳到right的起始位置,重新开始计算。
public int findLengthOfLCIS(int[] nums) {int left=0,right=0;int res=0;while(right < nums.length){//右侧的新元素比左侧小,则重新开始记录left的位置if(right > 0 && nums[right - 1] >= nums[right]){left = right;}right++;res=Math.max(res,right - left);}return res;
}
本题还有多种解法,另外一种思路是一边遍历,一边统计每个递增区间的长度,如果长度超过之前所有区间的长度,就将其保留,代码如下:
public int findLengthOfLCIS(int[] nums) {int curLen = 1;//当前递增区间的长度int res = 1;for(int i = 1;i < nums.length;i++){if(nums[i - 1] >= nums[i]){//不满足要求,重新进行数字计算curLen = 1;}else{curLen++;}res = Math.max(curLen,res);}return res;
}
可见就算不知道滑动窗口我们也能解决,所以滑动窗口就是个名字,不要被这些概念吓到。
END
本篇只是一个入门,很多时候往往存在即合理,这种思想一定在某个地方发挥着作用,我们下篇探讨!😎再见~
关注微信公众号:怒码少年。回复关键词【电子书】,领取多本计算机相关电子书
公众号后台开启了咨询业务,欢迎大家向我提问,免费,为爱发电😎




![[文件读取]shopxo 文件读取(CNVD-2021-15822)](https://img-blog.csdnimg.cn/9b3035be721947e5b78d090d6891996d.png)