在机器学习中，术语Ensemble指的是并行组合多个模型，这个想法是利用群体的智慧，在给出的最终答案上形成更好的共识。

这种类型的方法已经在监督学习领域得到了广泛的研究和应用，特别是在分类问题上，像RandomForest这样非常成功的算法。通常应用一些投票/加权系统，将每个单独模型的输出组合成最终的、更健壮的和一致的输出。

在无监督学习领域，这项任务变得更加困难。首先，因为它包含了该领域本身的挑战，我们对数据没有先验知识，无法将自己与任何目标进行比较。其次，因为找到一种合适的方法来结合所有模型的信息仍然是一个问题，而且对于如何做到这一点还没有达成共识。

在本文中，我们讨论关于这个主题的最佳方法，即相似性矩阵的聚类。

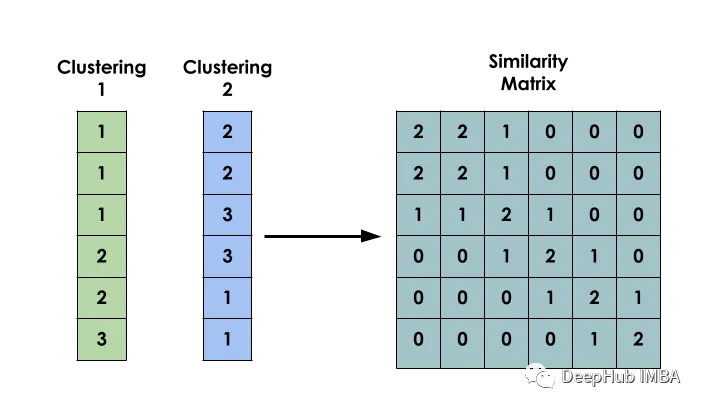
该方法的主要思想是：给定一个数据集X，创建一个矩阵S，使得Si表示xi和xj之间的相似性。该矩阵是基于几个不同模型的聚类结果构建的。

二元共现矩阵

构建模型的第一步是创建输入之间的二元共现矩阵。

它用于指示两个输入i和j是否属于同一个簇。

 import numpy as npfrom scipy import sparsedef build_binary_matrix( clabels ):data_len = len(clabels)matrix=np.zeros((data_len,data_len))for i in range(data_len):matrix[i,:] = clabels == clabels[i]return matrixlabels = np.array( [1,1,1,2,3,3,2,4] )build_binary_matrix(labels)

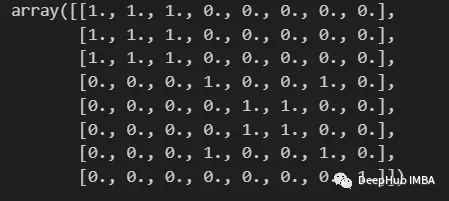
用KMeans构造相似矩阵

我们已经构造了一个函数来二值化我们的聚类，下面可以进入构造相似矩阵的阶段。

我们这里介绍一个最常见的方法，只包括计算M个不同模型生成的M个共现矩阵之间的平均值。定义为:

这样，落在同一簇中的条目的相似度值将接近于1，而落在不同组中的条目的相似度值将接近于0。

我们将基于K-Means模型创建的标签构建一个相似矩阵。使用MNIST数据集进行。为了简单和高效，我们将只使用10000张经过PCA降维的图像。

 from sklearn.datasets import fetch_openmlfrom sklearn.decomposition import PCAfrom sklearn.cluster import MiniBatchKMeans, KMeansfrom sklearn.model_selection import train_test_splitmnist = fetch_openml('mnist_784')X = mnist.datay = mnist.targetX, _, y, _ = train_test_split(X,y, train_size=10000, stratify=y, random_state=42 )pca = PCA(n_components=0.99)X_pca = pca.fit_transform(X)

为了使模型之间存在多样性，每个模型都使用随机数量的簇实例化。

 NUM_MODELS = 500MIN_N_CLUSTERS = 2MAX_N_CLUSTERS = 300np.random.seed(214)model_sizes = np.random.randint(MIN_N_CLUSTERS, MAX_N_CLUSTERS+1, size=NUM_MODELS)clt_models = [KMeans(n_clusters=i, n_init=4, random_state=214) for i in model_sizes]for i, model in enumerate(clt_models):print( f"Fitting - {i+1}/{NUM_MODELS}" )model.fit(X_pca)

下面的函数就是创建相似矩阵

 def build_similarity_matrix( models_labels ):n_runs, n_data = models_labels.shape[0], models_labels.shape[1]sim_matrix = np.zeros( (n_data, n_data) )for i in range(n_runs):sim_matrix += build_binary_matrix( models_labels[i,:] )sim_matrix = sim_matrix/n_runsreturn sim_matrix

调用这个函数：

 models_labels = np.array([ model.labels_ for model in clt_models ])sim_matrix = build_similarity_matrix(models_labels)

最终结果如下:

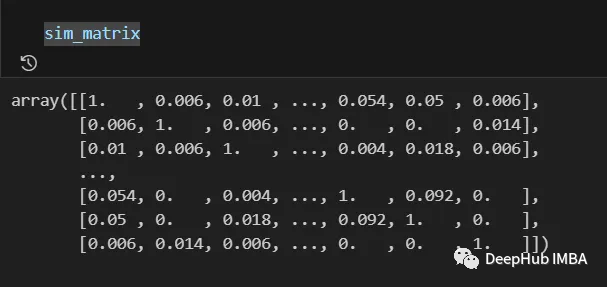
来自相似矩阵的信息在最后一步之前仍然可以进行后处理，例如应用对数、多项式等变换。

在我们的情况下，我们将不做任何更改。

 Pos_sim_matrix = sim_matrix

对相似矩阵进行聚类

相似矩阵是一种表示所有聚类模型协作所建立的知识的方法。

通过它，我们可以直观地看到哪些条目更有可能属于同一个簇，哪些不属于。但是这些信息仍然需要转化为实际的簇。

这是通过使用可以接收相似矩阵作为参数的聚类算法来完成的。这里我们使用SpectralClustering。

 from sklearn.cluster import SpectralClusteringspec_clt = SpectralClustering(n_clusters=10, affinity='precomputed',n_init=5, random_state=214)final_labels = spec_clt.fit_predict(pos_sim_matrix)

与标准KMeans模型的比较

我们来与KMeans进行性对比，这样可以确认我们的方法是否有效。

我们将使用NMI, ARI，集群纯度和类纯度指标来评估标准KMeans模型与我们集成模型进行对比。此外我们还将绘制权变矩阵，以可视化哪些类属于每个簇。

 from seaborn import heatmapimport matplotlib.pyplot as pltdef data_contingency_matrix(true_labels, pred_labels):fig, (ax) = plt.subplots(1, 1, figsize=(8,8))n_clusters = len(np.unique(pred_labels))n_classes = len(np.unique(true_labels))label_names =  np.unique(true_labels)label_names.sort()contingency_matrix = np.zeros( (n_classes, n_clusters) )for i, true_label in enumerate(label_names):for j in range(n_clusters):contingency_matrix[i, j] = np.sum(np.logical_and(pred_labels==j, true_labels==true_label))heatmap(contingency_matrix.astype(int), ax=ax,annot=True, annot_kws={"fontsize":14}, fmt='d')ax.set_xlabel("Clusters", fontsize=18)ax.set_xticks( [i+0.5 for i in range(n_clusters)] )ax.set_xticklabels([i for i in range(n_clusters)], fontsize=14)ax.set_ylabel("Original classes", fontsize=18)ax.set_yticks( [i+0.5 for i in range(n_classes)] )ax.set_yticklabels(label_names, fontsize=14, va="center")ax.set_title("Contingency Matrix\n", ha='center', fontsize=20)

 from sklearn.metrics import normalized_mutual_info_score, adjusted_rand_scoredef purity( true_labels, pred_labels ):n_clusters = len(np.unique(pred_labels))n_classes = len(np.unique(true_labels))label_names =  np.unique(true_labels)purity_vector = np.zeros( (n_classes) )contingency_matrix = np.zeros( (n_classes, n_clusters) )for i, true_label in enumerate(label_names):for j in range(n_clusters):contingency_matrix[i, j] = np.sum(np.logical_and(pred_labels==j, true_labels==true_label))purity_vector = np.max(contingency_matrix, axis=1)/np.sum(contingency_matrix, axis=1)print( f"Mean Class Purity - {np.mean(purity_vector):.2f}" ) for i, true_label in enumerate(label_names):print( f" {true_label} - {purity_vector[i]:.2f}" ) cluster_purity_vector = np.zeros( (n_clusters) )cluster_purity_vector = np.max(contingency_matrix, axis=0)/np.sum(contingency_matrix, axis=0)print( f"Mean Cluster Purity - {np.mean(cluster_purity_vector):.2f}" ) for i in range(n_clusters):print( f" {i} - {cluster_purity_vector[i]:.2f}" ) kmeans_model = KMeans(10, n_init=50, random_state=214)km_labels = kmeans_model.fit_predict(X_pca)data_contingency_matrix(y, km_labels)print( "Single KMeans NMI - ", normalized_mutual_info_score(y, km_labels) )print( "Single KMeans ARI - ", adjusted_rand_score(y, km_labels) )purity(y, km_labels)

 data_contingency_matrix(y, final_labels)print( "Ensamble NMI - ", normalized_mutual_info_score(y, final_labels) )print( "Ensamble ARI - ", adjusted_rand_score(y, final_labels) )purity(y, final_labels)

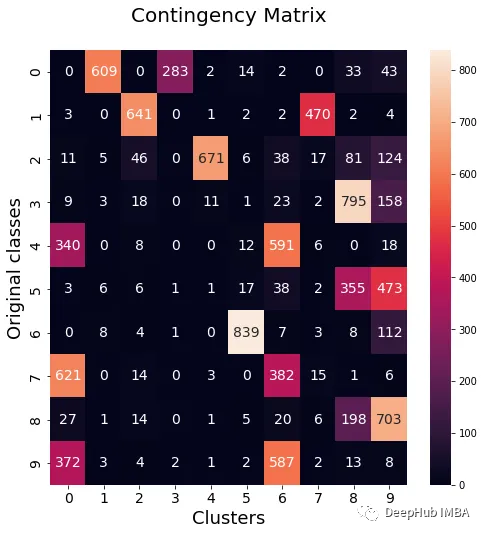
从上面的值可以看出，Ensemble方法确实能够提高聚类的质量。我们还可以在权变矩阵中看到更一致的行为，具有更好的分布类和更少的“噪声”。

本文引用

Strehl, Alexander, and Joydeep Ghosh. “Cluster ensembles — -a knowledge reuse framework for combining multiple partitions.” Journal of machine learning research 3.Dec (2002): 583–617.

Fred, Ana, and Anil K. Jain. “Combining multiple clusterings using evidence accumulation.” IEEE transactions on pattern analysis and machine intelligence 27.6 (2005): 835–850.

Topchy, Alexander, et al. “Combining multiple weak clusterings.” Third IEEE International Conference on Data Mining. IEEE, 2003.

Fern, Xiaoli Zhang, and Carla E. Brodley. “Solving cluster ensemble problems by bipartite graph partitioning.” Proceedings of the twenty-first international conference on Machine learning. 2004.

Gionis, Aristides, Heikki Mannila, and Panayiotis Tsaparas. “Clustering aggregation.” ACM Transactions on Knowledge Discovery from Data (TKDD) 1.1 (2007): 1–30.

https://avoid.overfit.cn/post/526bea5f183249008f77ccc479e2f555

作者：Nielsen Castelo Damasceno Dantas