树专题 —— 二叉搜索树和中序遍历

大家好，我是方圆。我准备把树写成一个专题，包括二叉搜索树、前序、中序、后序遍历以及红黑树，我也想试试能不能将红黑树写好。

本篇是关于二叉搜索树，也是所有后续学习的基础，其中会涉及前序、中序、后序遍历，后续再介绍相关遍历则是以题目为主。如果大家想要找刷题路线的话，可以参考 Github: LeetCode。

二叉搜索树

二叉搜索树（Binary Search Tree）是基础数据结构，在它是完全二叉树的情况下执行查找和插入的时间复杂度为 O(logn)，然而如果这棵树是一条 n 个节点做成的线性链表，那么这些操作的时间复杂度为 O(n)，它具备如下性质：

若任意节点的左子树不为空，则左子树上所有节点值 均小于 它的根节点值
若任意节点的右子树不为空，则右子树上所有节点值 均大于 它的根节点值
左子树为节点值均小于根节点的二叉搜索树；右子树为节点值均大于根节点的二叉搜索树

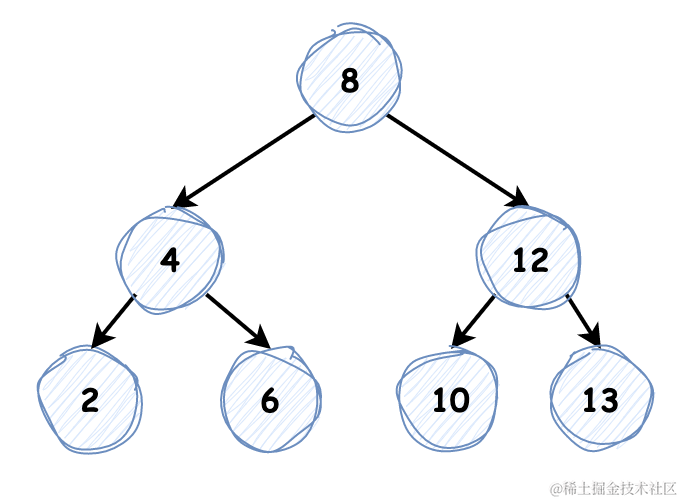
二叉搜索树.png

通过中序遍历我们能获取到二叉搜索树的有序序列，二叉树中序遍历模板如下：

    private void midOrder(TreeNode node) {if (node == null) {return;}midOrder(node.left);// do something...midOrder(node.right);}

中序遍历对节点的操作顺序是 “左根右”，恰好能以二叉搜索树节点值递增的顺序访问，二叉搜索树相关的题目大多与中序遍历有关，我们先看几道简单的题目：

注意：树相关的题目一般我们都会选择递归方法求解，但是大家千万不要把自己的脑袋当成计算机去模拟递归的过程，我们只需关注节点的递归顺序和在“当前”节点处所做的逻辑即可

1305. 两棵二叉搜索树中的所有元素

本题我们可以很轻松地将其解出来，分别用两个队列将两棵二叉搜索树中的节点值保存，之后根据大小关系将其合并到结果列表中即可，题解如下：

    public List<Integer> getAllElements(TreeNode root1, TreeNode root2) {LinkedList<Integer> queue1 = new LinkedList<>();LinkedList<Integer> queue2 = new LinkedList<>();midOrder(root1, queue1);midOrder(root2, queue2);List<Integer> res = new ArrayList<>();while (!queue1.isEmpty() || !queue2.isEmpty()) {if (queue1.isEmpty()) {res.add(queue2.poll());continue;}if (queue2.isEmpty()) {res.add(queue1.poll());continue;}if (queue1.peek() <= queue2.peek()) {res.add(queue1.poll());} else {res.add(queue2.poll());}}return res;}private void midOrder(TreeNode node, Queue<Integer> queue) {if (node == null) {return;}midOrder(node.left, queue);queue.offer(node.val);midOrder(node.right, queue);}

LCR 174. 寻找二叉搜索树中的目标节点

本题是查找二叉搜索树中的第 K 大节点，我们可以通过中序遍历将所有节点顺序保存下来再返回它的第 K 大节点，题解如下：

class Solution {List<Integer> nodes;public int findTargetNode(TreeNode root, int cnt) {nodes = new ArrayList<>();midOrder(root);return nodes.get(nodes.size() - cnt);}private void midOrder(TreeNode node) {if (node == null) {return;}midOrder(node.left);nodes.add(node.val);midOrder(node.right);}
}

230. 二叉搜索树中第K小的元素

我们再来看一道，本题也可以按照上一道题的思路来求解，不过在这里我们介绍一种更优的的方法：要求的是第 K 小节点，那么每经过一次节点将 K 减一，减到 0 时便是我们想要的节点，那么接下来我们便可以不再进行递归搜索了，避免了后续的无效递归，题解如下：

class Solution {int k;int res;public int kthSmallest(TreeNode root, int k) {this.k = k;midOrder(root);return res;}private void midOrder(TreeNode node) {if (node == null || k == 0) {return;}midOrder(node.left);k--;if (k == 0) {res = node.val;return;}midOrder(node.right);}
}

实现二叉搜索树

现在我们已经对二叉搜索树的性质有了基本的了解，接下来我们看看该如何实现一颗二叉搜索树。

定义 Node 节点类和 root 根节点的全局变量

public class BinarySearchTree {static class Node {int key;int val;Node left;Node right;public Node(int key, int val) {this.key = key;this.val = val;}}// 根节点Node root;}

查询节点值

查询方法的实现还是比较简单的，根据键值的大小关系来判断是去左子树、右子树还是返回当前节点值即可，代码如下：

    /*** 根据 key 获取对应的节点值*/public Integer getValue(int key) {return getValue(root, key);}private Integer getValue(Node node, int key) {if (node == null) {return null;}if (key > node.key) {return getValue(node.right, key);}if (key < node.key) {return getValue(node.left, key);}return node.val;}

插入节点

插入节点的方法和查询方法实现的逻辑基本一致，不过插入节点会 变换父节点对子节点的引用关系，第一个被插入的键就是根节点，第二个被插入的键则会根据大小关系成为根节点的左节点还是右节点，以此类推，代码实现如下：

    /*** 将节点插入二叉搜索树中合适的位置*/public void putNode(int key, int val) {root = putNode(root, key, val);}private Node putNode(Node node, int key, int val) {if (node == null) {return new Node(key, val);}if (key > node.val) {node.right = putNode(node.right, key, val);} else if (key < node.val) {node.left = putNode(node.left, key, val);} else {node.val = val;}return node;}

获取最大/最小节点

这两个方法比较简单，最大节点为右子树最大节点，最小节点为左子树最小节点：

    /*** 获取最大节点*/public Node getMaxNode() {if (root == null) {return null;}return getMaxNode(root);}private Node getMaxNode(Node node) {if (node.right == null) {return node;}return getMaxNode(node.right);}/*** 获取最小节点*/public Node getMinNode() {if (root == null) {return null;}return getMinNode(root);}private Node getMinNode(Node node) {if (node.left == null) {return node;}return getMinNode(node.left);}

向下取整查找

这个方法比较有意思，向下取整是查找小于等于 key 值的最大节点。如果给定的 key 小于根节点的值，那么小于等于 key 的最大节点一定在左子树中；如果给定的 key 大于根节点的值，那么小于等于 key 的最大节点可能在右子树中，当右子树中不存在小于等于 key 值的节点的话，最大节点就是根节点，否则为右子树中某节点，代码逻辑如下：

    /*** 向下取整查找*/public Node floor(int key) {return floor(root, key);}private Node floor(Node node, int key) {if (node == null) {return null;}if (key == node.val) {return node;}if (key < node.val) {return floor(node.left, key);}Node right = floor(node.right, key);return right != null ? right : node;}

向上取整查找

向上取整与向下取整的逻辑相反，我们把代码列在下面，具体的执行步骤大家思考一下：

    /*** 向上取整查找*/public Node ceiling(int key) {return ceiling(root, key);}private Node ceiling(Node node, int key) {if (node == null) {return null;}if (key == node.val) {return node;}if (key > node.val) {return ceiling(node.right, key);}Node left = ceiling(node.left, key);return left != null ? left : node;}

删除节点

删除节点在二叉搜索树中实现起来相对不容易，在实现删除任意节点之前，我们先写一下简单的删除最大/小值节点的方法。

删除最小节点

删除最小节点需要找到节点左子树为空树的节点，这个节点便是我们需要删除的最小节点，这个节点被删除后，我们需要将它的右子树拼接到它原来的位置，实现如下：

    /*** 删除最小节点*/public void deleteMin() {root = deleteMin(root);}private Node deleteMin(Node node) {if (node == null) {return null;}if (node.left == null) {return node.right;}node.left = deleteMin(root.left);return node;}

删除最大节点

该实现和删除最小节点的逻辑完全类似，如下：

    /*** 删除最大节点*/public void deleteMax() {root = deleteMax(root);}private Node deleteMax(Node node) {if (node == null) {return null;}if (node.right == null) {return node.left;}node.right = deleteMax(node.right);return node;}

删除指定节点

删除指定 key 值的节点我们需要先找到该节点，之后分情况讨论：

如果该节点左子树为空，那么需要将该节点的右子树拼接到该删除节点的位置；
如果该节点右子树为空，那么需要将该节点的左子树拼接到该删除节点的位置；
前两种情况和我们删除最值节点类似，第三种情况是该节点左右子树均不为空，那么我们可以找到该节点右子树的最小节点，并将该节点的左子树拼接到该最小节点的左子树上（同样地，我们也可以找到该节点左子树的最大节点，然后将该节点右子树拼接到该最大节点的右子树上），实现如下：

    /*** 删除指定节点*/public void delete(int key) {root = delete(key, root);}private Node delete(int key, Node node) {if (node == null) {return null;}if (key > node.val) {node.right = delete(key, node.right);return node;}if (key < node.val) {node.left = delete(key, node.left);return node;}if (node.left == null) {return node.right;}if (node.right == null) {return node.left;}Node min = getMinNode(node.right);min.left = node.left;return node;}

范围查找

二叉搜索树的范围查找实现很简单，只需根据大小条件关系中序遍历即可，实现如下：

    /*** 范围查找** @param left  区间下界* @param right 区间上界*/public List<Integer> keys(int left, int right) {ArrayList<Integer> res = new ArrayList<>();keys(root, left, right, res);return res;}private void keys(Node node, int left, int right, ArrayList<Integer> res) {if (node == null) {return;}if (node.val > left) {keys(node.left, left, right, res);}if (node.val >= left && node.val <= right) {res.add(node.val);}if (node.val < right) {keys(node.right, left, right, res);}}

总的来说，二叉搜索树的实现并不困难，大家最好将这些方法都实现一遍，以便更好的学习和理解。

相关习题

现在我们对二叉搜索树和中序遍历已经比较熟悉了，接下来再做一些题目来检查检查。在前文中我们已经说过，一般二叉搜索树的题目大概率会与中序遍历相关，此外，进行中序遍历时，有的题目需要我们 记录节点的“前驱节点” 来帮助解题，这一点需要注意。

235. 二叉搜索树的最近公共祖先

在二叉搜索树上找最近的公共祖先，我们分情况讨论：如果两节点值都比当前节点小的话，那么去左子树找；如果两节点值都比当前节点大的话，那么去右子树找；如果两节点中任意一节点等于当前节点或者两节点分别大于或小于当前节点的话，那么当前节点就是最近的公共祖先（大家可以画图看一下），题解如下：

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (p.val < root.val && q.val < root.val) {return lowestCommonAncestor(root.left, p, q);}if (p.val > root.val && q.val > root.val) {return lowestCommonAncestor(root.right, p, q);}return root;}

450. 删除二叉搜索树中的节点

本题和我们上述二叉搜索树删除节点的方法实现逻辑一致，只不过在这里我们获取右子树的最小节点时是通过迭代实现的，题解如下：

    public TreeNode deleteNode(TreeNode root, int key) {if (root == null) {return null;}if (key > root.val) {root.right = deleteNode(root.right, key);return root;}if (key < root.val) {root.left = deleteNode(root.left, key);return root;}if (root.right == null) {return root.left;}if (root.left == null) {return root.right;}TreeNode rightNode = root.right;while (rightNode.left != null) {rightNode = rightNode.left;}rightNode.left = root.left;return root.right;}

669. 修剪二叉搜索树

本题也是依赖二叉搜索树的性质来求解：

如果当前节点值比 low 小的话，那么需要将它修剪掉，并去它的右子树找满足区间条件的节点；
如果当前节点值比 high 大的话，那么也需要将它修剪掉，并去它的左子树找满足区间条件的节点；
如果当前节点值在区间范围内，则需要对它的左子树和右子树进行修剪，并将当前节点返回即可，题解如下：

    public TreeNode trimBST(TreeNode root, int low, int high) {if (root == null) {return null;}if (root.val < low) {return trimBST(root.right, low, high);}if (root.val > high) {return trimBST(root.left, low, high);}root.left = trimBST(root.left, low, high);root.right = trimBST(root.right, low, high);return root;}

98. 验证二叉搜索树

二叉搜索树需要满足根节点大于左子树任意节点和根节点小于右子树任意节点的性质，我们根据这个条件进行验证即可，需要注意的是：我们需要记录前驱节点来帮助比较节点的大小关系，题解如下：

    long pre = Long.MIN_VALUE;public boolean isValidBST(TreeNode root) {if (root == null) {return true;}boolean left = isValidBST(root.left);if (pre >= root.val) {return false;}pre = root.val;boolean right = isValidBST(root.right);return left && right;}

LCR 155. 将二叉搜索树转化为排序的双向链表

根据中序遍历的顺序拼接链表即可，可以为前驱节点创建哨兵节点，减少判空逻辑，题解如下：

    Node pre = null;public Node treeToDoublyList(Node root) {if (root == null) {return null;}Node head = new Node();pre = head;midOrder(root);head.right.left = pre;pre.right = head.right;return head.right;}private void midOrder(Node node) {if (node == null) {return;}midOrder(node.left);pre.right = node;node.left = pre;pre = node;midOrder(node.right);}

99. 恢复二叉搜索树

本题解题思路并不复杂，题目确定有两个节点发生了交换，那么我们通过两个指针对它们进行标记即可，题解如下：

    TreeNode one = null, two = null;TreeNode pre;public void recoverTree(TreeNode root) {midOrder(root);int temp = one.val;one.val = two.val;two.val = temp;}private void midOrder(TreeNode node) {if (node == null) {return;}midOrder(node.left);if (pre != null && pre.val > node.val) {if (one == null) {one = pre;}two = node;}pre = node;midOrder(node.right);}

面试题 04.06. 后继者

查找指定节点的后继节点，如果当前驱节点为指定节点时，那么当前节点即为所求的后继节点，题解如下：

    TreeNode pre = null;public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {if (root == null) {return null;}TreeNode left = inorderSuccessor(root.left, p);if (pre != null && pre.val == p.val) {pre = root;return root;}pre = root;TreeNode right = inorderSuccessor(root.right, p);return left == null ? right : left;}