数据结构：AVL树的旋转（平衡搜索二叉树）

1、AVL树简介

 AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。

  • 它的子树都是AVL树
  • 左右子树高度插（平衡因子）的绝对值不超过1

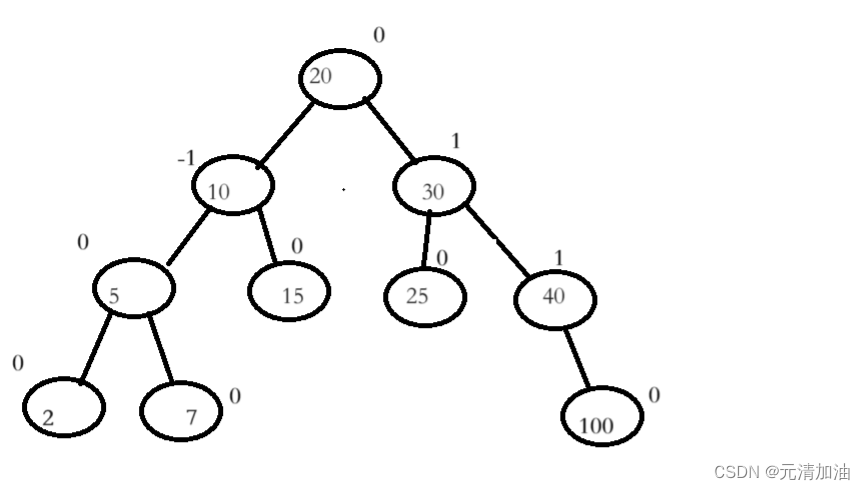
AVL树还是一个搜索二叉树，只不过因为普通的搜索二叉树有可能变成单只树，这样就使查找效率非常的低。我们就给普通的搜索二叉树增加了一个平衡因子来使AVL左右子树的高度差的绝对值不超过1

template<class K,class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;              pair<K, V> _kv;                          // 存储的键对int _bf;                                 // balance factorAVLTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv);bool IsBalance();void InOrder();void Height();private:void RotateL(Node* parent);              //左旋转void RotateR(Node* parent);              //右旋转void RotateRL(Node* parent);             //右左旋转void RotateLR(Node* parent);             //左右旋转bool _IsBalance(Node* root);void _InOrder(Node* root);int _Height(Node* root);Node* _root = nullptr;
};

2、AVL树的插入

  • AVL树的插入前面和搜索二叉树的插入一模一样，只不过我们要注意平衡因子
  • 因为AVL树保持平衡是要平衡因子的绝对值不超过1，而插入会使平衡因子改变，所以我们也要要相应的旋转，使平衡因子的绝对值不超过一，我们又有几种情况
  1. 假如以pParent为根的子树不平衡，即pParent的平衡因子为2或者-2，分以下情况考虑
  2. parent的平衡因子为2，说明parent的右子树高，设parent的右子树的根为subR，当subR的平衡因子为1时，执行左单旋。当subR的平衡因子为-1时，执行右左双旋
  3. parent的平衡因子为-2，说明parent的左子树高，设parent的左子树的根为subL，当subL的平衡因子为-1是，执行右单旋。当subL的平衡因子为1时，执行左右双旋
  4. 旋转完成后，原parent为根的子树个高度降低，已经平衡，不需要再向上更新
template<class K, class V>
bool AVLTree<K, V>::Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;// 更新平衡因子while (parent){if (cur == parent->_right){parent->_bf++;}else{parent->_bf--;}if (parent->_bf == 1 || parent->_bf == -1){// 继续更新parent = parent->_parent;cur = cur->_parent;}else if (parent->_bf == 0){break;}else if (parent->_bf == 2 || parent->_bf == -2){// 需要旋转处理 -- 1、让这颗子树平衡 2、降低这颗子树的高度if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{assert(false);}break;}else{assert(false);}}return true;
}

2.1、左单旋

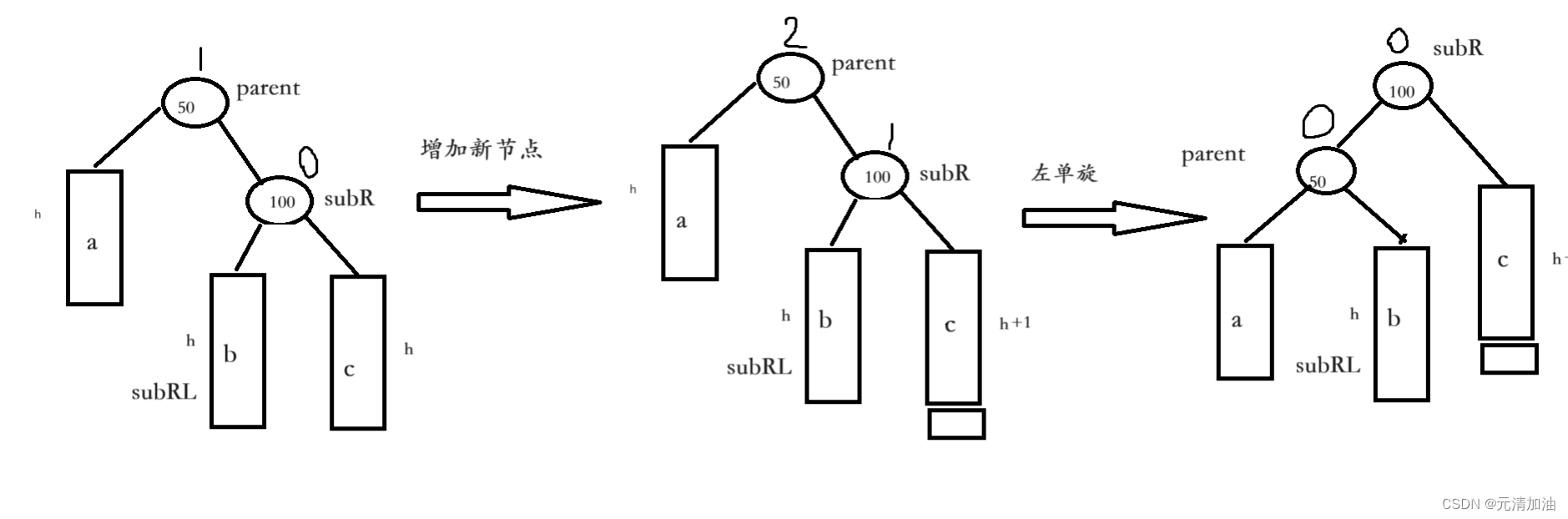
  1. subRL变成parent的右子树 
  2. parent变成subR的左子树
  3. subR变成新根
  4. 更新平衡因子
template<class K, class V>
void AVLTree<K, V>::RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* parentParent = parent->_parent;parent->_parent = subR;if (subRL)subRL->_parent = parent;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}parent->_bf = subR->_bf = 0;
}

2.2、右单旋

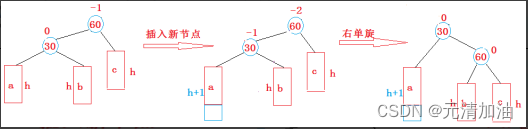
60为parent，30为subL，b为subLR 

  1. subLR变成parent的左子树 
  2. parent变成subL的右子树
  3. subL变成新根
  4. 更新平衡因子
template<class K, class V>
void AVLTree<K, V>::RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}subL->_bf = parent->_bf = 0;
}

2.3、左右双旋 

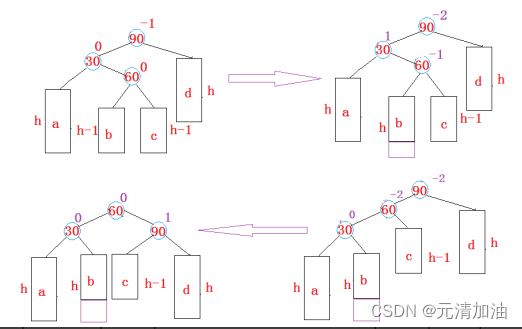
先对30进行左单旋，先对90右单旋

template<class K, class V>
void AVLTree<K, V>::RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = subL->_bf = subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0;}else if (bf == 1){parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else{assert(false);}
}

2.3、右左双旋 

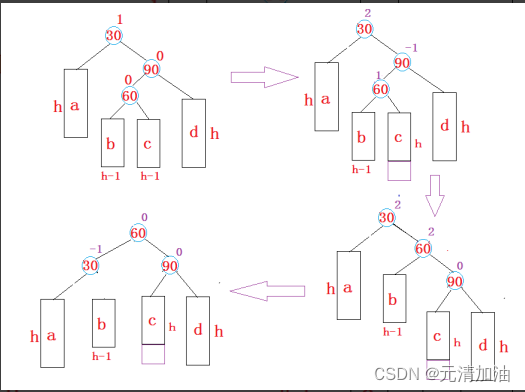
先对90进行右单旋，先对30左单旋 

template<class K, class V>
void AVLTree<K, V>::RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){// subRL自己就是新增parent->_bf = subR->_bf = subRL->_bf = 0;}else if (bf == -1){// subRL的左子树新增parent->_bf = 0;subRL->_bf = 0;subR->_bf = 1;}else if (bf == 1){// subRL的右子树新增parent->_bf = -1;subRL->_bf = 0;subR->_bf = 0;}else{assert(false);}
}

 3、AVL树的性能

AVL树是带有平衡条件的二叉查找树，一般是用平衡因子差值判断是否平衡并通过旋转来实现平衡，左右子树树高不超过1，和红黑树相比，它是严格的平衡二叉树，平衡条件必须满足（所有节点的左右子树高度差不超过1）。不管我们是执行插入还是删除操作，只要不满足上面的条件，就要通过旋转来保持平衡，而旋转是非常耗时的，由此我们可以知道AVL树适合用于插入删除次数比较少，但查找多的情况。

如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合

4、实现

#include<assert.h>template<class K,class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;              pair<K, V> _kv;                          // 存储的键对int _bf;                                 // balance factorAVLTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv);bool IsBalance();void InOrder();void Height();private:void RotateL(Node* parent);              //左旋转void RotateR(Node* parent);              //右旋转void RotateRL(Node* parent);             //右左旋转void RotateLR(Node* parent);             //左右旋转bool _IsBalance(Node* root);void _InOrder(Node* root);int _Height(Node* root);Node* _root = nullptr;
};template<class K, class V>
bool AVLTree<K, V>::Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;// 更新平衡因子while (parent){if (cur == parent->_right){parent->_bf++;}else{parent->_bf--;}if (parent->_bf == 1 || parent->_bf == -1){// 继续更新parent = parent->_parent;cur = cur->_parent;}else if (parent->_bf == 0){break;}else if (parent->_bf == 2 || parent->_bf == -2){// 需要旋转处理 -- 1、让这颗子树平衡 2、降低这颗子树的高度if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{assert(false);}break;}else{assert(false);}}return true;
}template<class K, class V>
void AVLTree<K, V>::RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* parentParent = parent->_parent;parent->_parent = subR;if (subRL)subRL->_parent = parent;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}parent->_bf = subR->_bf = 0;
}template<class K, class V>
void AVLTree<K, V>::RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}subL->_bf = parent->_bf = 0;
}template<class K, class V>
void AVLTree<K, V>::RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){// subRL自己就是新增parent->_bf = subR->_bf = subRL->_bf = 0;}else if (bf == -1){// subRL的左子树新增parent->_bf = 0;subRL->_bf = 0;subR->_bf = 1;}else if (bf == 1){// subRL的右子树新增parent->_bf = -1;subRL->_bf = 0;subR->_bf = 0;}else{assert(false);}
}template<class K, class V>
void AVLTree<K, V>::RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = subL->_bf = subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0;}else if (bf == 1){parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else{assert(false);}
}template<class K, class V>
void AVLTree<K, V>::InOrder()
{_InOrder(_root);cout << endl;
}template<class K, class V>
void AVLTree<K, V>::_InOrder(Node* root)
{if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);
}template<class K, class V>
bool AVLTree<K, V>::IsBalance()
{return _IsBalance(_root);
}template<class K, class V>
int AVLTree<K, V>::_Height(Node* root)
{if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}template<class K, class V>
void AVLTree<K, V>::Height()
{cout << _Height(_root) << endl;
}template<class K, class V>
bool AVLTree<K,V>::_IsBalance(Node* root)
{if (root == nullptr)return true;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return abs(rightHeight - leftHeight) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/135225.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

flutter项目引入本地静态图片资源并展示

flutter项目引入本地静态图片资源并展示

想要在flutter中引入静态资源&#xff0c;需要配置pubspec.yaml&#xff0c;将本地的静态资源添加到assets下面&#xff1a; 然后在flutter引入这些静态资源&#xff1a; Image.asset("images/squick.png") 就可以在app中看到这个图片了&#xff1a; 也可以使用网…
阅读更多...
falsk框架中安装flask-mysqldb报错解决方案

falsk框架中安装flask-mysqldb报错解决方案

错误示例 我的是py37版本&#xff0c;无法直接安装flask-mysqldb pip install flask-mysqldb报错如下 解决方案 先去第三方库 https://www.lfd.uci.edu/~gohlke/pythonlibs/#mysqlclient 下载mysqlclient 这个是我的版本 mysqlclient-1.4.6-cp37-cp37m-win_amd64.whl 下…
阅读更多...
C++ [继承]

C++ [继承]

本文已收录至《C语言和高级数据结构》专栏&#xff01; 作者&#xff1a;ARMCSKGT 继承 前言正文继承的概念及定义继承的概念继承的定义重定义 基类和派生类对象赋值转换派生类中的默认成员函数隐式调用显示调用 继承中的友元与静态成员友元静态成员 菱形继承概念 虚继承原理继…
阅读更多...
react组件通信

react组件通信

目录 前言&#xff1a; 父子组件通信 子父组件通信 兄弟组件通信 总结 前言&#xff1a; React是一种流行的JavaScript库&#xff0c;用于构建现代化的、高性能的Web应用程序。在React中&#xff0c;组件是代码的构建块。组件通信是React中一个非常重要的概念&#xff0c;…
阅读更多...
Kafka反序列化RCE漏洞（CVE-2023-34040）

Kafka反序列化RCE漏洞（CVE-2023-34040）

漏洞描述 Spring Kafka 是 Spring Framework 生态系统中的一个模块&#xff0c;用于简化在 Spring 应用程序中集成 Apache Kafka 的过程&#xff0c;记录 (record) 指 Kafka 消息中的一条记录。 受影响版本中默认未对记录配置 ErrorHandlingDeserializer&#xff0c;当用户将…
阅读更多...
Bean的四种实例化方式以及BeanFactory和FactoryBean的区别

Bean的四种实例化方式以及BeanFactory和FactoryBean的区别

2023.11.8 Spring为Bean提供了多种实例化方式&#xff0c;通常包括4种方式。 第一种&#xff1a;通过构造方法实例化第二种&#xff1a;通过简单工厂模式实例化第三种&#xff1a;通过factory-bean实例化第四种&#xff1a;通过FactoryBean接口实例化 通过构造方法实例化 创…
阅读更多...
android display 笔记（三）WMS

android display 笔记（三）WMS

用来记录学习wms&#xff0c;后续会一点一点更新。。。。。。 代码&#xff1a;android14 WMS是在SystemServer进程中启动的 在SystemServer中的main方法中&#xff0c;调用run方法。 private void run() { // Initialize native services.初始化服务&#xff0c;加载andro…
阅读更多...
FreeRTOS_空闲任务

FreeRTOS_空闲任务

目录 1. 空闲任务详解 1.1 空闲任务简介 1.2 空闲任务的创建 1.3 空闲任务函数 2. 空闲任务钩子函数详解 2.1 钩子函数 2.2 空闲任务钩子函数 3. 空闲任务钩子函数实验 3.1 main.c 空闲任务是 FreeRTOS 必不可少的一个任务&#xff0c;其他 RTOS 类系统也有空闲任务&a…
阅读更多...
广东开放大学：电大搜题助力学子迎考利器

广东开放大学：电大搜题助力学子迎考利器

近年来&#xff0c;广东开放大学一直致力于为广大学子提供优质的教育资源和学习服务。作为一所专注于远程教育的学府&#xff0c;广东开放大学不仅拥有雄厚的师资力量和丰富的教育经验&#xff0c;还致力于创新教学手段&#xff0c;为学生提供更便捷、高效的学习体验。在这个信…
阅读更多...
2023年11月在线IDE流行度最新排名

2023年11月在线IDE流行度最新排名

点击查看最新在线IDE流行度最新排名&#xff08;每月更新&#xff09; 2023年11月在线IDE流行度最新排名 TOP 在线IDE排名是通过分析在线ide名称在谷歌上被搜索的频率而创建的 在线IDE被搜索的次数越多&#xff0c;人们就会认为它越受欢迎。原始数据来自谷歌Trends 如果您相…
阅读更多...
08.Diffusion Model数学原理分析（上）

08.Diffusion Model数学原理分析（上）

文章目录 Diffusion Model回顾Diffusion Model算法TrainingInference 图像生成模型的本质目标MLE vs KLVAE计算 P θ ( x ) P_\theta(x) Pθ​(x)Lower bound of log ⁡ P ( x ) \log P(x) logP(x) DDPM计算 P θ ( x ) P_\theta(x) Pθ​(x)Lower bound of log ⁡ P ( x ) \…
阅读更多...
数据结构与算法-(11)---有序表(OrderedList)

数据结构与算法-(11)---有序表(OrderedList)

&#x1f308;个人主页: Aileen_0v0 &#x1f525;系列专栏:PYTHON学习系列专栏 &#x1f4ab;"没有罗马,那就自己创造罗马~" 目录 知识回顾及总结 有序表的引入 ​编辑 实现有序表 1.有序表-类的构造方法 2.有序表-search方法的实现 3.有序表-add方法的实现…
阅读更多...
【技术类-01】doc转PDF程序卡死的解决方案，

【技术类-01】doc转PDF程序卡死的解决方案，

摘要&#xff1a; 1、出现 raise AttributeError("%s.%s" % (self._username_, attr))&#xff09; 2、表现&#xff1a;doc转PDF卡死&#xff08;白条不动或出现以上英文&#xff09; 3、解决&#xff1a;在docx保存代码行后面加上time.sleep(3) 4、原因&#x…
阅读更多...
SpringBoot系列之集成Redission入门与实践教程

SpringBoot系列之集成Redission入门与实践教程

Redisson是一款基于java开发的开源项目&#xff0c;提供了很多企业级实践&#xff0c;比如分布式锁、消息队列、异步执行等功能。本文基于Springboot2版本集成redisson-spring-boot-starter实现redisson的基本应用 软件环境&#xff1a; JDK 1.8 SpringBoot 2.2.1 Maven 3.2…
阅读更多...
Java进阶篇--线程池之FutureTask

Java进阶篇--线程池之FutureTask

目录 FutureTask简介 FutureTask的基本使用 FutureTask的应用场景 FutureTask简介 FutureTask是Java中的一个类&#xff0c;用于表示可获取结果的异步任务。它实现了java.util.concurrent.Future接口&#xff0c;提供了启动和取消异步任务、查询任务是否已完成以及获取最终…
阅读更多...
腾讯云3年云服务器价格及购买教程

腾讯云3年云服务器价格及购买教程

腾讯云作为国内领先的云计算服务提供商&#xff0c;提供了多种优惠的云服务器套餐&#xff0c;以满足不同用户的需求&#xff0c;本文将详细介绍腾讯云3年云服务器价格及购买教程&#xff0c;新老用户均可购买&#xff01; 1、活动页面&#xff1a;传送门>>> 2、进入…
阅读更多...
P3379 【模板】最近公共祖先（LCA）

P3379 【模板】最近公共祖先（LCA）

洛谷里面8页题解千篇一律&#xff0c;就没有用线段树求解的&#xff0c;这下不得不由本蒟蒻来生啃又臭又硬&#xff0c;代码又多的线段树了。 样例的欧拉序列&#xff1a;4 2 4 1 3 1 5 1 4 记录每个节点最早在欧拉序列中的时间&#xff0c;任意两个节点的LCA就是他们两个节点…
阅读更多...
Flink -- 状态与容错

Flink -- 状态与容错

1、Stateful Operations 有状态算子&#xff1a; 有状态计算&#xff0c;使用到前面的数据&#xff0c;常见的有状态的算子&#xff1a;例如sum、reduce&#xff0c;因为它们在计算的时候都是用到了前面的计算的结果 总结来说&#xff0c;有状态计算并不是独立存在的&#xf…
阅读更多...
ssh免密登录

ssh免密登录

单机 1 生成密钥 执行 ssh-keygen -t rsa &#xff08; 其中 rsa 是非对称算法&#xff09; 一路回车到底&#xff0c;生成密钥 且生成之后会在用户的根目录生成一个 “.ssh”的文件夹 2 添加公钥到 将 公钥内容追加到 authorized_keys 中&#xff1a; cat ~/.ssh/id_rsa.pub …
阅读更多...
汽车网络安全渗透测试概述

汽车网络安全渗透测试概述

目录 1.汽车网络安全法规概述 1.1 国外标准 1.2 国内标准 2.汽车网络安全威胁分析 2.1 汽车网络安全资产定义 2.2 汽车网络安全影响场景及评级示例 3.汽车网络安全渗透测试描述 3.1 参考法规 3.2 渗透测试内容 4.小结 1.汽车网络安全法规概述 近年来&#xff0c;汽车…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023