数据结构之树(Tree)
目录
- 树的基本概念
- 树的分类
- 树的基本操作
- 树的应用
- 结语
树的基本概念
树是一种重要的数据结构,它在计算机科学中被广泛应用。树的特点是以分层的方式存储数据,具有层次结构,类似于现实生活中的树状结构。在树中,每个节点都有一个父节点,除了根节点没有父节点,每个节点可以有多个子节点。
-
节点(Node):树中的每个元素称为一个节点,每个节点存储一个数据元素。
-
度(degree): 一个节点的子树的个数称为该节点的度数,一棵树的度数是指该树中节点的最大度数。
-
根节点(Root):树的顶部节点称为根节点,它是树的唯一入口。
-
父节点(Parent):每个节点除了根节点外,都有一个父节点,父节点是指向当前节点的节点。
-
子节点(Child):每个节点可以有零个或多个子节点,子节点是指被当前节点所指向的节点。
-
叶节点(Leaf):没有子节点的节点称为叶节点,也称为终端节点。
-
深度(Depth):树中节点的层次数称为深度,根节点的深度为0,其余节点的深度为其父节点的深度加1。
-
高度(Height):树中节点的最大深度称为树的高度。
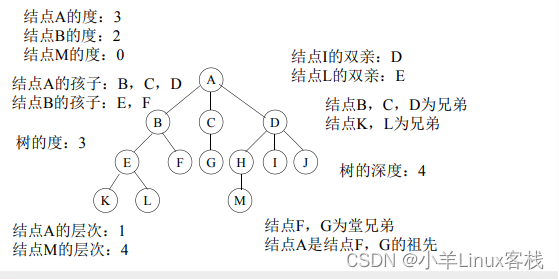
树的逻辑结构 : 树中任何节点都可以有零个或多个直接后继节点(子节点),但至多只有一个直接前趋节点(父节点),根节点没有前趋节点,叶节点没有后继节点。
树的分类
树可以根据其结构和特点进行不同的分类,常见的树包括:
-
二叉树(Binary Tree):每个节点最多有两个子节点,分别是左子节点和右子节点。
-
二叉搜索树(Binary Search Tree, BST):一种特殊的二叉树,左子树中的所有节点都小于根节点,右子树中的所有节点都大于根节点。
-
平衡二叉树(Balanced Binary Tree):一种特殊的二叉搜索树,左右子树的高度差不超过1,保证了较快的查找性能。
-
红黑树(Red-Black Tree):一种自平衡二叉搜索树,通过一系列规则保持树的平衡。
-
AVL树:一种自平衡二叉搜索树,通过旋转操作保持树的平衡。
-
B树(B-tree):一种多叉树,用于存储大量数据,常用于数据库索引结构。
树的基本操作
-
插入节点:向树中添加新节点。
-
删除节点:从树中删除指定节点。
-
查找节点:在树中查找指定节点。
-
遍历树:按照某种规则遍历树的所有节点。
-
求树的深度和高度:计算树的深度和高度。
树的应用
树在计算机科学中有广泛的应用,包括但不限于以下方面:
-
文件系统:文件系统通常使用树的结构来组织文件和目录。
-
数据库索引:数据库索引使用树的结构来快速查找数据。
-
表达式求值:表达式求值可以使用树的结构来构建表达式树,并进行计算。
-
人工智能:人工智能中的决策树、神经网络等算法都涉及到树的应用。
-
编译器:编译器中的语法分析阶段常常使用树的结构来构建抽象语法树。
结语
树作为一种重要的数据结构,不仅在计算机科学中有广泛的应用,也是算法和数据结构学习中的重要内容。通过学习树的概念、分类和基本操作,我们可以更好地理解树在计算机领域的应用,并在问题解决中灵活运用。希望本篇博客能够帮助读者对树有更深入的认识,并在学习和工作中发挥作用。如有任何问题或疑问,请随时留言。
:CNN和cifar10二)

)









)






